
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нахождение собственных значений и собственных векторов
|
|
|
|
Собственные значения и собственные векторы матрицы  удовлетворяют матричному уравнению
удовлетворяют матричному уравнению 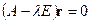 .
.
Если  собственный вектор матрицы
собственный вектор матрицы  , то однородная система
, то однородная система  имеет нетривиальное решение, поэтому
имеет нетривиальное решение, поэтому 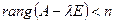 (
(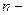 порядок матрицы
порядок матрицы 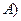 и
и 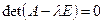 .
.
Последнее уравнение позволяет найти собственные значения матрицы  .
.
Определение. Многочлен 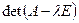 называют характеристическим многочленом матрицы
называют характеристическим многочленом матрицы  .
.
Определение. Уравнение

называется характеристическим уравнением матрицы  .
.
Корни характеристическогоуравнения матрицы  являются собственными значениями матрицы
являются собственными значениями матрицы  .
.
Характеристическое уравнение матрицы  может быть записано в виде
может быть записано в виде 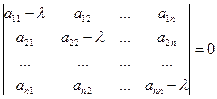 .
.
Определение. Множество всех собственных значений квадратной матрицы называется спектром этой матрицы.
Спектр матрицы  -го порядка содержит
-го порядка содержит  собственных значений матрицы, которые могут быть как действительными, так и комплексными, простыми так и кратными.
собственных значений матрицы, которые могут быть как действительными, так и комплексными, простыми так и кратными.
Для матрицы 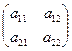 характеристическое уравнение
характеристическое уравнение 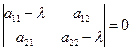 может быть может быть преобразовано к виду
может быть может быть преобразовано к виду 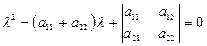 .
.
 , поэтому характеристическое уравнение матрицы
, поэтому характеристическое уравнение матрицы 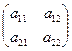 имеет вид
имеет вид
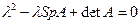 . (8.1)
. (8.1)
При этом
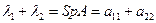 , (8.2)
, (8.2)
 . (8.3)
. (8.3)
Уравнение 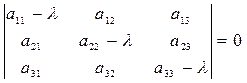 является характеристическим уравнением матрицы
является характеристическим уравнением матрицы 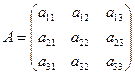 .
.
Это уравнение может быть представлено в виде

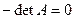 или
или
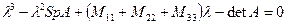 , (8.4)
, (8.4)
где 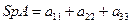 , а
, а 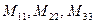 миноры определителя
миноры определителя  .
.
Если 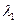 ,
, 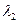 и
и 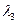 корни характеристического уравнения (8.4), то это уравнение может быть записано в виде
корни характеристического уравнения (8.4), то это уравнение может быть записано в виде
 . (8.5)
. (8.5)
Сравнивая уравнения (8.4) и (8.5), можно записать следующее:
 , (8.6)
, (8.6)
 , (8.7)
, (8.7)
 . (8.8)
. (8.8)
Собственные векторы матрицы  , соответствующие собственному значению
, соответствующие собственному значению 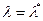 , удовлетворяют матричному уравнению
, удовлетворяют матричному уравнению 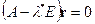 , которое может быть записана в форме
, которое может быть записана в форме 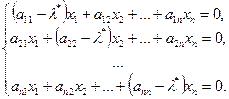
Так как ранг матрицы этой системы меньше числа неизвестных (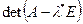 =0), то система имеет бесконечное множество
=0), то система имеет бесконечное множество
решений, каждое ненулевое из которых является собственным вектором, соответствующим собственному значению 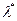 .
.
|
|
|
● Пример 5. Найти собственные значения и собственные векторы матрицы  .
.
Решение. 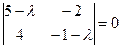 - характеристическое уравнение для данной матрицы, откуда
- характеристическое уравнение для данной матрицы, откуда  ,
, 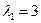 и
и  .
.
Для нахождения собственных векторов, соответствующих собственному значению 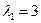 , имеем систему
, имеем систему 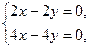 эквивалентную уравнению
эквивалентную уравнению 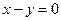 . Вектор
. Вектор  является решением этого уравнения, а при
является решением этого уравнения, а при 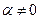 вектор
вектор 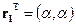 - искомый собственный вектор.
- искомый собственный вектор.
Для нахождения собственных векторов, соответствующих собственному значению  , имеем систему
, имеем систему 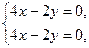 из которой следует, что вектор
из которой следует, что вектор  при
при 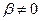 является собственным вектором, соответствующим собственному значению
является собственным вектором, соответствующим собственному значению  .
.
Ответ. 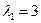 ,
, 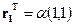 при
при 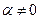 ;
;
 ,
, 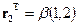 при
при 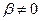 .
.
● Пример 6.
Найти собственные пары матрицы 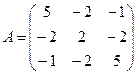 .
.
Решение.  - характеристическое уравнение матрицы
- характеристическое уравнение матрицы  , которое может быть записано в виде
, которое может быть записано в виде 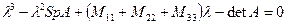 , где
, где
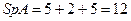 ,
, 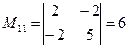 ,
,  ,
, 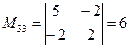 ,
,  (проверьте).
(проверьте).
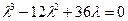 - характеристическое уравнение матрицы
- характеристическое уравнение матрицы  , корни которого
, корни которого 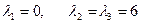 .
.
Собственные векторы, соответствующие собственному значению 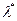 , находим из системы
, находим из системы 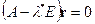 .
.
При  имеем систему
имеем систему 
которая равносильна системе 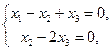 решение которой
решение которой  .
.
При 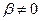 вектор
вектор  является собственным вектором матрицы
является собственным вектором матрицы  , соответствующим собственному значению
, соответствующим собственному значению  .
.
При  для нахождения собственных векторов имеем систему
для нахождения собственных векторов имеем систему 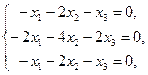 которая равносильна одному уравнению
которая равносильна одному уравнению 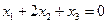 .
.
При любых 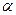 и
и 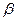 вектор
вектор 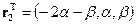 есть решение уравнения
есть решение уравнения 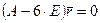 , а при
, а при 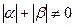
 является собственным вектором, который соответствует собственному значению
является собственным вектором, который соответствует собственному значению 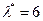 .
.
Ответ:  при
при 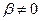 ;
;  при
при 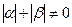 .
.
● Пример 7. Найти собственные значения и собственные векторы матрицы 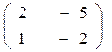 .
.
Решение. Характеристическое уравнение для указанной матрицы имеет вид  , откуда
, откуда 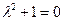 и
и  .
.
Для нахождения собственных векторов, соответствующих собственному значению 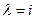 , имеем систему
, имеем систему  из которой следует
из которой следует  при
при 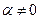 .
.
Для нахождения собственных векторов, соответствующих собственному значению 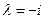 , имеем систему
, имеем систему  из которой следует
из которой следует  при
при 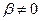 .
.
Ответ. 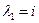 ,
,  при
при 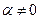 ;
;
 ,
,  при
при 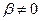 .
.
● Пример 8.
Доказать, что если 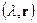 собственная пара невырожденной матрицы
собственная пара невырожденной матрицы  , то
, то  -собственная пара матрицы
-собственная пара матрицы  .
.
|
|
|
► Так матрица  невырожденная (
невырожденная ( ), то существует
), то существует  . Произведение собственных значений матрицы
. Произведение собственных значений матрицы  равно
равно 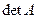 , а так как
, а так как  , то собственное значение
, то собственное значение 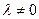 .
.
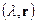 -собственная пара матрицы
-собственная пара матрицы  , поэтому
, поэтому 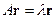 . Умножив последнее равенство слева на
. Умножив последнее равенство слева на  , имеем
, имеем  , откуда
, откуда 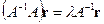 ,
,  и
и 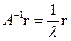 . Последнее равенство означает, что
. Последнее равенство означает, что  -собственная пара матрицы
-собственная пара матрицы  .◄
.◄
|
|
|
|
|
Дата добавления: 2015-07-02; Просмотров: 533; Нарушение авторских прав?; Мы поможем в написании вашей работы!