Частица в яме конечной глубины

В разделе 4.2 мы рассмотрели движение частицы в потенциальных ямах с бесконечно высокими стенками. Переход к анализу движения частицы в яме конечной глубины будем проводить поэтапно и сначала рассмотрим частицу в потенциальной яме с одной бесконечно высокой стенкой (рис.4.18). Такая задача представляет практический интерес, поскольку потенциальная энергия двух частиц, между которыми действуют силы притяжения, например, двух атомов, образующих молекулу, по виду близка к рассматриваемой модели.

Рис. 4.18.

Одномерная яма с одной бесконечно высокой стенкой. Рассмотрим частицу, движущуюся в одномерной потенциальной яме вида

При меньше 0 потенциальная энергия частицы бесконечна и волновая функция , как мы уже знаем, обращается в нуль. Поэтому уделим основное внимание при решении данной задачи исследованию движения частицы в области .

Обозначим цифрой I область , а цифрой II - область . Рассмотрим сначала случай, при котором полная энергия частицы , т.е. будем считать, что частица находится в потенциальной яме. Уравнение Шредингера (4.6) в области I имеет вид

(4.56)

а в области II

(4.57)

Вводя обозначения

(4.58)

приводим уравнения (4.56) и (4.57) к виду

(4.59a)

(4.59b)

Решая уравнения (4.59), находим и

(4.60a)

(4.60b)

Воспользуемся условиями, налагаемыми на волновую функцию. Поскольку волновая функция должна быть всюду конечной, а первое слагаемое в (4.60b) при неограниченно возрастает, то необходимо потребовать, чтобы коэффициент был равен нулю, т.е. чтобы .

Перейдем теперь к анализу граничных условий. Непрерывность волновой функции на левой границе ямы приводит, как мы уже видели в разделе 4.2, к соотношению , откуда следует, что . Условие сшивки волновых функций и их производных при дает следующую систему уравнений

(4.61)

Разделив первое уравнение (4.61) на второе, приходим к соотношению

(4.62)

которое и определяет энергетический спектр частицы в яме.

Ввиду того, что уравнение (4.62) является трансцендентным, получить значения энергии частицы 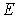в явном виде не удается. Покажем с помощью графического метода, что энергетический спектр частицы, определяемый соотношением (4.62) с учетом (4.58), является дискретным, т.е. энергия частицы в яме квантуется.

Уравнение (4.62) легко преобразуется к виду

(4.63)

Построим графики левой и правой частей уравнения (4.63) как функции параметра . Точки пересечения синусоиды с прямой (рис.4.19)

Рис. 4.19.

определяют корни уравнения (4.63), отвечающие искомым значениям энергии частицы . Поскольку, согласно (4.62), , то будем выбирать только те значения параметра , которые удовлетворяют условию

где = 0, 1, 2, 3,... На рис.4.19 соответствующие области значений на оси абсцисс выделены жирной линией.

Приведенные графики показывают, что энергетический спектр частицы является дискретным. Чем больше глубина 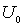и ширина потенциальной ямы, тем ниже наклон прямой в правой части уравнения (4.63) и тем больше точек пересечения имеет прямая с синусоидой. Следовательно, тем больше энергетических уровней помещается в потенциальной яме.

Найдем условия, при которых в яме существует хотя бы один энергетический уровень. В этом случае коэффициент, определяющий наклон прямой в правой части уравнения (4.63), должен удовлетворять неравенству

Выражая отсюда , получаем

(4.64)

Обсудим это соотношение подробнее. Именно при выполнении этого условия уравнение Шредингера для частицы в яме имеет решение, т.е. в яме имеется хотя бы один энергетический уровень. Говорят, что в этом случае существует связанное состояние частицы в яме. Отметим, что в левую часть неравенства (4.64) входят только параметры потенциальной ямы - ее ширина и глубина 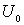, а правая часть для рассматриваемого типа частиц (значения ) представляет собой константу.

Если потенциальная яма недостаточно глубока или недостаточно широка, так что условие (4.64) не выполняется, то уравнение Шредингера для частицы в яме не имеет решения, или, как говорят, в яме не помещается ни одного энергетического уровня. В физике такие случаи достаточно хорошо известны. Так, например, между двумя нейтронами или между двумя протонами действуют ядерные силы притяжения, однако связанного состояния двух нейтронов или двух протонов в природе не существует - потенциальная яма, соответствующая взаимодействию этих частиц, имеет недостаточную ширину и глубину.

Сила взаимодействия между протоном и нейтроном лишь незначительно превышает силу взаимодействия для двух протонов или двух нейтронов, однако этого превышения оказывается достаточно, чтобы появилось связанное состояние нейтрона и протона - дейтрон. В потенциальной яме, характеризующей взаимодействие протона с нейтроном, помещается лишь один энергетический уровень. Это означает, что дейтрон всегда находится в основном состоянии и не имеет возбужденных состояний.

Вернемся к анализу волновых функций данной задачи. При , как уже отмечалось, . В области I, т.е. в потенциальной яме, волновая функция имеет вид

что означает, что уравнение Шредингера, как и в случае ямы с двумя бесконечно высокими стенками, имеет осциллирующее решение. Наибольший интерес представляет вид волновой функции в области II

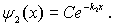
Волновая функция вне потенциальной ямы отлична от нуля и спадает с расстоянием по экспоненциальному закону, а это означает, что существует отличная от нуля вероятность пребывания частицы вне потенциальной ямы (см. задачу 4.7). Соотношение между константами и находятся из условия нормировки волновой функции. Качественный вид волновых функций для данной задачи приведен на рис. 4.20.

Рис. 4.20.

Рассмотрим теперь случай . Уравнение Шредингера в областях I и II, соответственно, имеет вид

(4.65a)

и

(4.65b)

где

Решение уравнения (4.65a) с учетом условия на границе ямы есть

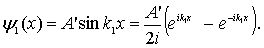
(4.66)

Решение уравнения (4.65b) представим в виде

(4.67)

Производя сшивку волновых функций и их производных в точке , приходим к следующей системе уравнений

Решая эту систему относительно амплитуд и , получаем их выражения через амплитуду

(4.68)

Отметим, что соотношения (4.68) определяют амплитуды и при любых значениях и 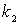, т.е. при любом значении энергии частицы

. Это означает, что при частица имеет непрерывный спектр энергии.

Обсудим вид волновых функций (4.66) и (4.67). Каждая их них представляет собой сумму двух волн де Бройля: волны , распространяющейся слева направо, и волны , распространяющейся слева направо. Пришедшая из волна (второе слагаемое в (4.67)) на границе ямы частично отражается, давая вклад в первое слагаемое в (4.67), и преломляется (второе слагаемое в (4.66)). Далее волна отражается от стенки при (первое слагаемое в (4.66)), опять преломляется на границе ямы , давая вклад в первое слагаемое в (4.67), и уходит на бесконечность.

Дата добавления: 2015-06-27