Э.Д.С. индукции в движущихся проводниках

При включении источника тока, лампочка, включенная последовательно с катушкой, загорается со значительным запозданием по сравнению с лампочкой, включенной последовательно с реостатом.

Размыкая и замыкая магнитную цепь, то есть меняя индуктивность, можно добиться таких же результатов, как и при замыкании и размыкании электрической цепи.

При размыкании электрической цепи можно добиться того, что ЭДС самоиндукции значительно превысит ЭДС источника тока.

При замыкании электрической цепи, ток в ней должен принимать максимальное значение не мгновенно, а спустя некоторое время.

Пронаблюдать эти эффекты можно на следующих установках.

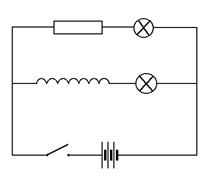
Соберем две электрические цепи. Одна состоит из последовательно соединенных электролампочки и проволочной катушки со стальным сердечником. Другая - из электролампочки и реостата. Сопротивление реостата равно сопротивлению проволоки, из которой изготовлена катушка. Реостат необходим для уравнивания накала лампочек, которые одновременно могут подключаться к источнику тока.

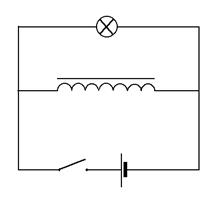
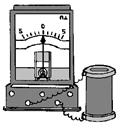
Подключим к источнику тока параллельно соединенные проволочную катушку с замкнутым стальным сердечником и электролампочку. Установим в цепи такое напряжение, чтобы лампочка горела неполным накалом. При размыкании цепи, соединяющей катушку с источником тока, в катушке возникает ЭДС, значительно превышающая ЭДС источника тока, о чем свидетельствует яркая вспышка лампочки.

На второй установке можно пронаблюдать и эффекты, возникающие при замыкании и размыкании магнитной цепи.

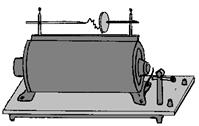
Индукционные эффекты, возникающие в цепях с большими индуктивностями, при их замыкании и размыкании, находят очень широкое применение. Одним из приборов, где используется эффект размыкания электрической цепи, является индукционная катушка.

Действительно, ЭДС самоиндукции, возникающая при размыкании электрической цепи, может принимать очень большие значения. Индукционная катушка, подключенная к аккумулятору, имеющему ЭДС порядка нескольких вольт, позволяет получить ЭДС в несколько десятков тысяч вольт, достаточную для пробоя слоя воздуха длиной несколько сантиметров.

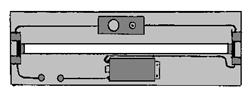
Катушки с большой индуктивностью позволяют получить ЭДС самоиндукции, значительно превышающую напряжение осветительной сети и тем самым зажечь люминесцентные лампы дневного света.

Закон электромагнитной индукции гласит, что ЭДС индукции, возникающая в проводящем контуре, прямо пропорциональна скорости изменения магнитного потока, пронизывающего этот контур.

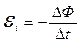, где .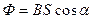

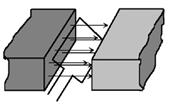
В опытах, приведших нас к закону электромагнитной индукции, найти этот контур нетрудно. В одном случае он образован витками проволочной катушки, в другом — алюминиевым кольцом, в третьем — рамкой, вращающейся в магнитном поле. Во всех случаях мы имеем дело с изогнутыми проводниками, охватывающими какую-то площадь, пронизываемую магнитным полем.

Но может возникнуть вопрос: а нельзя ли придумать такую ситуацию, чтобы ЭДС индукции возникала в прямом проводнике?

Ответ на этот вопрос связан с разрешением противоречия. С одной стороны, прямой провод принципиально не может образовывать контура. С другой стороны, он этот контур образовать должен.

 

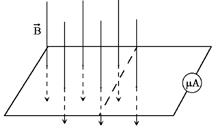
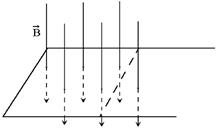
Разрешить противоречие можно, представив себе такую ситуацию. Пусть прямой проводник, подсоединенный с помощью проводов к какому-то индикатору тока (например, микроамперметру), движется в магнитном поле, пересекая линии магнитной индукции под некоторым углом, отличным от нуля. При соответствующем расположении, проводник, подводящие провода и микроамперметр могут образовать искомый контур, площадь которого за счет движения проводника будет меняться. Соответственно, раз этот контур пронизывается магнитным полем, будет меняться магнитный поток, проходящий через него, в контуре возбудится ЭДС индукции и так, как цепь замкнута, возникнет индукционный ток.

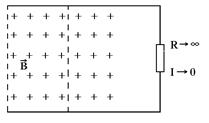
Если в цепь включить резистор с очень большим, в идеале бесконечно большим сопротивлением, что будет эквивалентно разрыву цепи, индукционный ток в ней прекратится, но ЭДС, вероятно, будет индуцироваться по-прежнему.

 

 

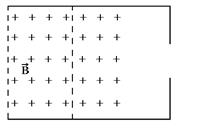
Формально, контур, площадь которого при движении проводника изменяется, остался. Фактически он перестал существовать, так как бесконечно большим сопротивлением может обладать и очень маленький зазор в контуре, который с геометрических позиций практически ничего в нем не меняет, и весь участок, подсоединенный к прямому проводнику, исключение которого лишает смысла само понятие «контур».

Таким образом, в прямом проводнике, пересекающем при своем движении силовые линии магнитного поля, должна индуцироваться ЭДС, так же, как и в проводящем контуре при изменении магнитного потока, пронизывающего его.

Описать эту ситуацию можно, например, так: проводник, движущийся в магнитном поле не параллельно его силовым линиям, «ометает» некоторую площадь, величина которой меняется. Следовательно, меняется и магнитный поток, пронизывающий ометаемую площадь. За счет этого, в проводнике индуцируется ЭДС.

Величина индуцируемой ЭДС может быть найдена из следующих соображений.

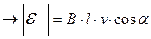
Где: l - длина проводника, находящегося в магнитном поле;

x - перемещение проводника в магнитном поле за время D t;

a - угол между вектором магнитной индукции и нормалью к плоскости, ограниченной ометаемым контуром;

v - скорость движения проводника.

Если ввести угол b - между направлением скорости движения проводника и вектором магнитной индукции, то

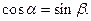
С учетом этого:

.

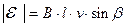Знак ЭДС можно определить по правилу Ленца.

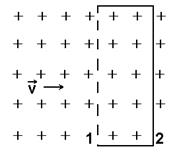
Пусть проводник движется в плоскости листа, а силовые линии магнитного поля входят в эту плоскость сверху вниз.

Мысленно восстановим контур, две стороны которого образованы двумя последовательными положениями движущегося проводника. Если бы этот контур был проводящим, в нем возник бы индукционный ток. Представим, что этот ток действительно возникает.

При движении проводника в любую сторону, ометаемая им площадь увеличивается, увеличивается и магнитный поток через ометаемую площадь.

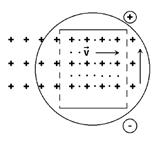
Чтобы противодействовать увеличению этого магнитного потока, индуцированное магнитное поле (по нашим представлениям порожденное индукционным током) должно быть направлено в сторону, противоположную полю, в котором движется проводник. Направление индукционного тока, который бы возник в контуре, определяется по правилу буравчика или правого винта. Силовые линии индуцированного магнитного поля выходят из листа. На чертеже они изображены точками.

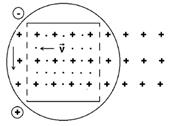
Для нашего случая, ручка выкручиваемового из плоскости листа вверх буравчика движется против часовой стрелки и показывает, что в проводнике, движущемся справа налево индукционный ток пошел бы сверху вниз, за счет чего положительные заряды скопились бы в нижней части проводника, а отрицательные, соответственно, в верхней. В проводнике же, движущемся слева направо, наоборот, индукционный ток пошел снизу вверх и привел к скоплению положительных зарядов в верхней части проводника, а отрицательных зарядов — в нижней части.

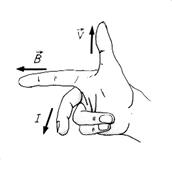
Знак ЭДС можно определить и по правилу правой руки, которое вытекает из правила Ленца.

Большой, указательный и средний пальцы правой руки располагают перпендикулярно друг другу. Большой палец направляют вдоль скорости движения проводника, а указательный вдоль вектора индукции магнитного поля. Тогда средний палец укажет направление движения в проводнике положительных зарядов и, соответственно, тот конец проводника, где они скопятся.

Объяснить появление ЭДС индукции в движущемся в магнитном поле проводнике, получить уравнение для расчета величины этой ЭДС и определить ее знак можно еще одним способом.

В проводнике имеются свободные заряженные частицы. Если эти частицы вместе с проводником движутся в магнитном поле, то на них со стороны магнитного поля действует сила Лоренца

, где

q - заряд каждой свободной частицы, перемещающейся вдоль проводника под действием магнитного поля;

v - скорость движения частиц в магнитном поле, равная скорости движения проводника;

В - величина индукции магнитного поля;

b - угол между направлением вектора скорости движения частицы (проводника) и вектора индукции магнитного поля.

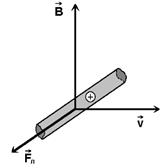
Если проводник движется таким образом, что пересекает линии индукции магнитного поля, то направление силы Лоренца определяется по правилу левой руки. Она оказывается направленной вдоль проводника и приводит в нем к разделению зарядов: положительные заряды накапливаются на одном конце проводника, отрицательные — на другом.

Так, если проводник движется вправо, вектор индукции магнитного поля направлен вдоль листа бумаги снизу вверх, то сила Лоренца, действующая на положительные заряды, направлена из плоскости листа вверх.

Если проводник разомкнут, то разделение зарядов будет происходить до тех пор, пока сила Лоренца не уравновесится электрической силой, возникающей при этом разделении.

Сила Лоренца совершает работу по разделению зарядов и является силой неэлектрического происхождения. Такие силы называются сторонними, они приводят к появлению в проводнике ЭДС.

ЭДС — это физическая величина, определяемая отношением работы сторонних сил по перемещению заряда, к величине этого заряда:

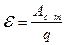, где

В данном случае F - сила Лоренца, l - длина проводника, вдоль которого движется частица под действием силы Лоренца.

Подставляя в определяющее уравнение значение силы Лоренца имеем:

,

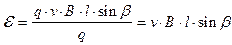что совпадает с полученным выше выражением.

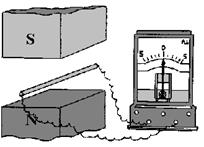
Проверить правильность полученного выражения для ЭДС индукции в движущихся проводниках и знак ЭДС можно на опыте.

Поскольку ЭДС должна зависеть от скорости движения проводника, индукции магнитного поля, длины проводника, находящегося в магнитном поле и его ориентации, необходимо последовательно меняя только одну из этих величин, а остальные оставляя постоянными, исследовать влияние этих изменений на величину возникающей в проводнике ЭДС. Знак ЭДС можно определить с помощью вольтметра путем прямого измерения.

Дата добавления: 2015-06-27