Абстрактные формальные системы

Дальнейшие примеры формальных систем. Исторически формальные системы создавались с конкретной целью более точного обоснования методов построения математических теорий. Однако постепенно стало ясно, что на основе тех же принципов — исходного набора аксиом, правил вывода и понятия выводимости — можно описывать не только мно­жества выражений, интерпретируемых как высказывания, но и перечислимые множества объектов произвольного вида. Основы теории ¹ таких формальных систем были заложены

¹ Начиная с этого момента понятие «теория» употребляется в обыч­ном интуитивном смысле и не имеет прямого отношения к точному понятию «формальной теории», рассмотренному в предыдущих парагра­фах.

Э. Постом. Эту теорию можно назвать абстрактной (хотя этот термин и не является общепринятым) или общей, так как она — в отличие от метатеории логических исчислений— не рассматривает свойства формальных систем относительно их конкретных интерпретаций, а изучает лишь их внутрен­ние, синтаксические свойства.

Прежде чем перейти к самой теории, рассмотрим некото­рые примеры формальных систем, не связанных с логиче­скими интерпретациями.

Пример 6-6. а. Множество допустимых шахматных пози­ций можно описать как формальную систему, в которой единственной аксиомой является начальная позиция, пра­вилами вывода — правила игры, а теоремами — позиции, полученные по правилам игры из начальной. Однако эта идея требует уточнения. Пусть дана позиция, скажем, ее диаграмма или описание в шахматной нотации. Для того чтобы однозначно получить все позиции, достижимые из данной за один ход, недостаточно знать правила хода всех фигур, в том числе правила взятия и правило превра­щения пешки; может понадобиться информация, не содержа­щаяся явно в позиции: нужно знать: 1) чей ход; 2) ходил ли раньше король (если он стоит на своем начальном поле, позиция на этот вопрос не отвечает) — это нужно для опре­деления допустимости рокировки; 3) не был ли последний ход ходом пешки через два поля - это нужно для определе­ния взятия пешки на проходе. Чтобы превратить множество шахматных позиций в формальную систему, нужно за пози­цию принять такое ее описание, которое в явном виде содер­жит ответы на все три вопроса. Для исключения позиций, получающихся после взятия королей, надо ввести правила, запрещающие игнорировать шах, и понятие заключитель­ных позиций (матовых и патовых), после которых никакие ходы не разрешаются.

б. Многие индуктивные определения можно превратить в формальные системы, аксиомы которых перечислены в ба­зисе (первом пункте) определения, а правила вывода — в индуктивном шаге. Необходимым условием перехода к фор­мальной системе является конструктивность задания аксиом и правил вывода, точнее, разрешимость множества аксиом и отношения непосредственной выводимости.

Рассмотрим, например, индуктивное определение абстрактной ориентированной двухполюсной схемы.

1) Пусть зафиксировано конечное число объектов, кото­рые назовем элементами; в каждом элементе выделено два полюса: вход и выход. Элементы являются схемами, полюсы которых совпадают с полюсами схем.

2) Пусть S₁ и S₂ — схемы. Тогда объекты, получаю­щиеся:

а) путем отождествления выхода S₁ со входом S₂ (правило последовательного соединения) и

б) путем отождествления входа S₁. со входом S₂ и выхода S_l с выходом S₂ (правило параллельного соеди­нения), также являются схемами. В случае 2а входом схемы является вход S₁ выходом — выход S₂. В случае 26 вхо­дом является объединенный вход S₁, S₂, выходом: — объе­диненный выход S₁, S₂.

Это определение описывает формальную систему, в ко­торой аксиомам являются элементы с выделенными полю­сами, а правилами вывода — правила соединения схем. Любой инженер даст этой системе обычную схемную (в ин­женерном смысле слова — как правило, электротехниче­скую) интерпретацию; однако такая интерпретация вовсе не вытекает из определения. В понятие элемента не вклады­вается никакого содержания; единственное, что от него требуется — возможность эффективно распознавать по­люсы. Элементом может быть ориентированное ребро, по­люсы которого — вершины; тогда схемы — это просто графы с выделенным входом (источником) и выходом (сто­ком). (Вопрос к читателю: все ли такие графы порождаются данной формальной системой?) Другая возможная интерпре­тация: элементы — одноместные функции; последовательное соединение — композиция функций, т. е. их последова­тельное вычисление, а параллельное соединение — парал­лельное вычисление двух функций с одинаковыми исходными данными и суммированием результатов в конце.

При описании формальных систем в примере 6-6 была допущена одна вольность, которая, строго говоря, недопу­стима. Дело в том, что ни в одном из этих описаний не за­фиксирован алфавит; соответственно и правила вывода не сформулированы как операции над символами в словах. Можно, конечно, сказать, что «примерно понятно, как это сделать; детали не уточняются», но способы уточнения мо­гут быть различными и приведут к различным формальным системам. Это обстоятельство известно всем, кто занимался программированием игры в шахматы или машинными пре­образованиями схем. Да и вообще любой, кто программиро­вал содержательно сформулированные алгоритмы, знает, что начинатъ приходится с выбора формы представления данных, т. е. символического кодирования объектов в тер­минах языка программирования (а в случае автокода — просто машинными словами), причем различные выборы приводят к формальным системам, совершено различным по своему виду и качествам. Этот выбор — предыстория формальной системы, возникающей лишь тогда, когда он уже сделан.

Общая теория формальных систем не рассматривает все возможные свойства конкретных систем, подобно тому, как теория алгоритмов не учит строить конкретные алго­ритмы. Одной из ее главных целей является цель, в некото­ром смысле противоположная: выяснить, каков необходи­мый минимум средств, с помощью которых можно описать любую формальную систему. Сюда же примыкает вопрос, центральный для любой математической теории: каковы возможности объектов, изучаемых в данной теории? Для теории формальных систем он выглядит так: какие множе­ства могут порождаться формальными системами? Опыт изучения теории алгоритмов говорит о том, что такого рода задачи решаются путем выбора конкретных средств, приво­дящих к конкретным моделям, общность которых показы­вается затем путем сравнения их с другими моделями. Средства формальных систем — это аксиомы и правила вы­вода. В абстрактных формальных системах, в отличие от логических исчислений, не выделяется понятия формулы («осмысленного выражения»); их объекты — произвольные слова в фиксированном алфавите. Итак, формальная система FS определяется: 1) алфавитом А (множество всех слов в алфавите А обозначим A*); 2) разрешимым множеством A₁ 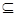А*, элементы которого называются аксиомами; 3) ко­нечным множеством вычислимых отношений R_i (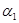,......, 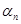, ) на множестве А*, называемых правилами вы­вода ¹; слово называется выводимым из 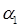,..., 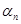по правилу R_i. Понятия вывода, выводимости и доказатель­ства — те же, что и для формальных теорий (см. § 6-1).

Иногда, впрочем, конкретное множество аксиом в си­стеме не фиксируется, а рассматривается выводимость из произвольных разрешимых множеств слов; в этом случае понятия вывода и доказательства не различаются. Конкрет-

¹ Аксиомы также можно задать правилом вывода (одноместным отношением): R_i ( ) ~” — аксиома».

ные виды формальных систем определяются в основном ви­дом правил вывода. Здесь будут рассмотрены два способа представления формальных систем: системы подстановок и системы продукций Поста. Однако уже общего определе­ния формальной системы оказывается достаточным, чтобы получить простой, но важный факт.

Теорема 6-14. Для любой формальной системы FS множество всех доказуемых в ней слов перечислимо.

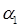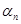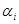Рассмотрим множество А** всех конечных последова­тельностей ,..., , где — слова в алфавите А. Множе­ство А**, очевидно, перечислимо. Ввиду разрешимости множества аксиом и вычислимости правил вывода по лю­бой последовательности 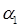,..., 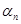можно эффективно узнать, является она выводом в FS или нет. Поэтому если в процессе перечисления А** выбрасывать все последовательности 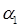,..., , 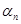не являющиеся выводами, то получим перечис­ление множества выводов. Следовательно, множество по­следних слов выводов, т. е. слов, выводимых в FS, пере­числимо. D

Отметим, что описанная процедура перечисляет выводи­мые слова, вообще говоря, с повторениями, поскольку одно и то же выводимое слово может иметь много выводов (на­пример, любая последовательность, заканчивающаяся акси­омой, есть вывод этой аксиомы).

Верно ли обратное — можно ли для перечислимого мно­жества М построить перечисляющую его формальную систему, т. е. систему, в которой множество выводимых слов совпадает с М? Из предварительных соображений можно ответить утвердительно: представляется, например, прав­доподобным, что машину Тьюринга можно проинтерпрети­ровать как формальную систему. Точный ответ на этот вопрос будет дан при рассмотрении конкретных видов фор­мальных систем.

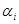
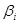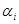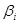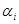
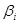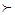
Системы подстановок. Система подстановок, или полу­система Туэ — это формальная система, определяемая алфавитом А и конечным множеством подстановок вида где , —слова, возможно, пустые, в А. Под­становка интерпретируется как правило вывода R_i следующим образом: 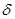по правилу R_i, если слово 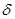получается из путем подстановки слова 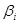вместо какого-нибудь вхождения 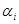в слово . Выводом из в системе подстановок называется цепочка 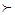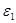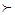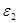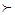... 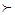, где каждое 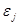получается из 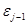некоторой подстановкой; как и обычно, наличие выводимости обозначаем .

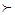
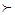
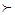
Такое определение вывода отличается от определения в на­чале § 6-1; предоставляем читателю убедиться, что для лю­бой формальной системы, где все правила — бинарные и унарные отношения, эти два определения совпадают, т. е. в первом смысле, если и только если во вто­ром смысле. (Заметим, что правило заключения в логиче­ских исчислениях — тернарное отношение!)

Зафиксируем множество аксиом системы и назовем слово 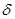заключительным, если оно доказуемо в системе и к нему неприменима ни одна из подстановок, т. е. если никакое его подслово не является левой частью никакой подстановки. Системе команд 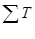машины Тьюринга Т нетрудно поста­вить в соответствие систему подстановок S_T над конфигура­циями; фактически это уже было сделано при построении универсальной машины Тьюринга (§ 5-2). Если в качестве аксиом выбрать слова q₁ , то заключительными словами в системе S_T будут слова q_z (, — слова в алфавите ленты машины Т). Если же к S_T добавить подстановку q_z , то в полученной системе 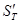множество заключительных слов совпадает с множеством значений функции, вычисляемой машиной Т. Это дает для систем подстановок теорему, обрат­ную теореме 6-14.

Теорема 6-15. Для любого перечислимого множествам существует система подстановок, множество заключительных слов которой совпадает с М. D

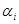
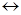
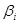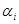
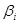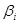
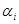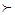
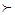
Ассоциативное исчисление, или система Туэ — это фор­мальная система, определяемая алфавитом А и конечным множеством соотношений , каждое из которых по­нимается как пара подстановок (левая подста­новка) (правая подстановка). Таким образом, ассоциативное исчисление всегда есть система подстановок; обратное, вообще говоря, неверно. При наличии таких парных правил вывода, если , то и ; ввиду отме­ченной ранее транзитивности выводимости получаем, что в ассоциативном исчислении выводимость является отноше­нием эквивалентности и разбивает множество всех слов в A на классы эквивалентности. Заключительные слова в ассоциативных исчислениях возможны, однако они соот­ветствуют классам эквивалентности, состоящим из одного слова, и особого интереса не представляют.

Аналогично тому, как это делалось для систем подстано­вок, поставим в соответствие каждой машине Тьюринга Т (будем считать, что Т работает на правой полуленте) ассо- циативное исчисление S (Т). Опишем это соответствие более подробно. Если А т — алфавит ленты машины Т, то A_S = А_T U {q₁, …, q_z}. Системе команд машины T соответ­ствует система соотношений в S (Т) (слева — команды, справа — соотношения):

q_ia_j q_ka_lR; q_ia_j 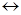a_lq_k; (6-13)
q_ia_j q_ka_lL; а_tq_ia_j 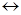q_ka_ta_l для всех a_t 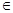А_т (6-14)

(число соотношений, соответствующих одной команде с дви­жением влево, равно | А_т|).

Теорема 6-16. В исчислении S (Т) слова q_ia_j и q_za_k 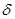эквивалентны, если и только если машина Т из конфигура­ции q_ia_j за конечное число тактов переходит в конфигу­рацию q_za_k .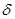

Одна половина теоремы («если») непосредственно сле­дует из доказательства теоремы 6-15. Вторая половина («толкко если») может показаться несколько неожиданной: ведь в S(Т) допускаются подстановки в обе стороны, а в Т— в одну и, следовательно, возможности S(Т) выглядят более, сильными. Тем не менее покажем, что если существует вывод q_ia_j |— q_za_k 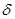, то машина Т из конфигурации q_ia_j переходит в конфигурацию q_za_k 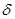. Рассмотрим этот вывод, т. е. цепочку q_ia_j |— |—... 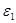|— q_za_k 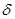. Каждое слово в этой цепочке получено из предыдущего либо левой, либо правой подстановкой. Кроме того, символ q в каждом слове — единственный. Последнее слово не может быть полу­чено правой подстановкой, так как символ q_z отсутствует в левых частях команд машины Т. Пусть 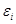— последнее слово в цепочке, полученное правой подстановкой: 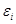= 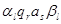. Слово 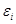получено из 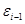правой подстанов­кой, т. е. применением одного из соотношений (6-13), (6-14), содержащим q_ra_s в левой части. Но таких соотношений столько, сколько команд Т с q_ra_s в левой части, т. е. ровно одно; обозначим его E_rs. Слово 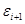получено из 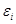левой подстановкой (по условию для 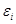); но единственная левая подстановка, применимая к 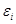, — это то же соотношение E_rs (точнее, его левая половина). Итак, к 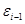применено E_rs слева направо, а к результату этого применения 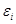применено то же E_rs справа налево. Так как все подстановки (6-13), (6-14) содержат q, а в любом слове цепочки q един­ственно, то любая подстановка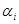 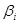к любому слову 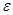может быть применена единственным образом, т. е. в 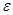найдется не более чем одно вхождение 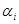. Отсюда 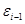= 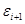, поэтому 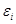и 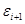из цепочки можно выбросить и по­строить вывод q_ia_j |—… |—... 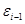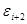|— q_za_k 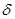, в ко­тором слов, полученных правой подстановкой, на единицу меньше, чем в прежнем выводе. Применяя к новому выводу те же рассуждения, из него также можно удалить слово, полученное правой подстановкой; в конечном счете будет построен вывод q_ia_j … q_za_k 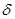, содержащий только левые подстановки, т. е. в точности воспроизводящий после­довательность конфигураций машины Т. D

Теорема 6-17 (теорема Маркова — Поста). Существует ассоциативное исчисление, в котором проблема распозна­вания эквивалентности слов алгоритмически неразрешима.

Возьмем какую-нибудь универсальную машину Тью­ринга U, которая является правильно вычисляющей, т. е. начинает с конфигураций вида q₁ и заканчивает работу конфигурациями вида q_z . Для машины U проблема оста­новки неразрешима (иначе ввиду универсальности U была бы разрешима общая проблема остановки для машин Тью­ринга). Построим ассоциативное исчисление S (U) и присое­диним к нему систему соотношений вида q_za_i 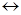q_z; получим новое исчисление S' (U). В этом исчислении, так же как и в S(U), можно имитировать вычислительный процесс U, однако благодаря новым соотношениям все заключитель­ные конфигурации U в S' (U) эквивалентны q_z. Поэтому теорема 6-16 для S' (U) имеет следующий вид: в S(U) слова q₁ . и q_z эквивалентны, если и только если U, начав с q₁ , остановится. Ввиду неразрешимости проблемы остановки для U проблема эквивалентности q₁ и q_z также нераз­решима. D

Ассоциативные исчисления имеют важную алгебраическую интер­претацию. В гл. 2 говорилось о том, что всякую полугруппу можно получить из свободной полугруппы (т. е. просто из множества А* всех слов в алфавите А) введением -определяющих соотношений, т. е. равенств 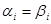. Замена полслова 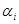в слове равным ему полсловом 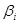, т. е. переход от слова 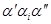к слову 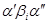, называется эквивалент­ным преобразованием слова . Слова считаются равными (или эквива­лентными), если они могут быть получены друг из друга цепочкой эквивалентных преобразований.

Содержательно эквивалентность слов означает, что они задают один и тот же элемент полугруппы; иначе говоря, элементами полу­группы, заданной определяющими соотношениями, являются классы эквивалентности слов, порождаемые этими соотношениями. Формально такое описание полугруппы — это просто ассоциативное исчисление с соотношениями 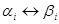; эквивалентные преобразования в полугруппе — это выводы в исчислении. В гл. 2 была сформулирована проблема эквивалентности слов в полугруппе. Теперь становится ясным, что ответ на нее — это просто переформулировка теоремы 6-17.

Теорема 6-17. Существует полугруппа, заданная определяющими соотношениями, в которой проблема распознавания эквивалентности (равенства) слов алгоритмически неразрешима. D

Г. С. Цейтин нашел очень простое ассоциативное исчисление с нераз­решимой "проблемой равенства — с алфавитом из пяти букв {а, b, с, d, e} и семью соотношениями:

ас 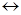са; ad 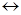da; bc 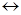cb; bd 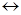db; abac 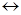abace; eca 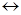ae;

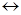edb be.

Теорема 6-17 явилась исторически первым примером доказатель­ства алгоритмической неразрешимости проблемы, не связанной с ло­гикой и основаниями математики.

Дата добавления: 2015-06-27