Эвристическая оценочная функция для И-ИЛИ графов

Эвристический поиск на И-ИЛИ графах

Поиск в глубину на И-ИЛИ графе

Как по И-ИЛИ графу построить решающее дерево? Это дело системы (стратегии) управления. На И-ИЛИ графах возможны все виды поиска, которые мы изучили: поиск в глубину, поиск в ширину, эвристический поиск.

Поиск в глубину на И-ИЛИ графах является процедурным механизмом Prolog-системы. Вначале системе адресуется запрос, или главная цель.

Для ее решения нужно решить все подцели в теле правила, с которым запрос сопоставился. Это вершина типа «И».

Если к цели могут быть применены альтернативные правила, то это вершина типа «ИЛИ».

Цель, которая сопоставилась с фактом базы данных, — терминальная вершина.

Рассмотрим поиск в глубину на модельном И-ИЛИ графе (рис. 19):

Рисунок 19. Модельный «И-ИЛИ граф»

Поиск в глубину из вершины X:

Если Х-целевая вершина, то задача решена.

Если Х-вершина типа «ИЛИ», то нужно пробовать решать одну за другой задачи-преемники, пока не будет найдена задача, имеющая решение.

Если Х-вершина типа «И», то нужно решить все ее задачи-преемники.

Если применение этих правил не приводит к решению, то решения нет.

Задание. Написать программу, реализующую поиск в глубину на модельном И-ИЛИ графе (рис. 19). Какова ее вычислительная сложность?

Припишем дугам И-ИЛИ графа стоимости.

Положим стоимость решающего дерева равной стоимости входящих в него дуг.

Цель оптимизации — поиск дерева решения минимальной стоимости.

Определим стоимость вершины как стоимость минимального решающего дерева с корнем в этой вершине.

Определим эвристическую функцию на вершинах И-ИЛИ графа. Эвристическая оценка листов равна непосредственно значению эвристики h(u) на вершине u. Внутренние вершины имеют преемников. Они будут оцениваться с помощью возвращенной эвристической оценки — оценки стоимости минимального решающего дерева с корнем в u.

— оценка для ИЛИ-вершины (рис. 20).

Рисунок 20. Возвращенная эвристика «ИЛИ»-вершины

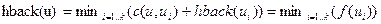
— оценка для И-вершины (рис. 21).

Рисунок 21. Возвращенная эвристика «И»-вершины

3) — оценка для листа

В нашем дереве поиска у каждой вершины только один отец. Пусть u₀ — отец, u — сын (рис.22).

Рисунок 22. f-оценка сына u₁ с отцом u₀

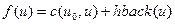
f-оценка вершины u складывается как стоимость дуги, входящей в u от родительской вершины, плюс ее возвращенная эвристическая оценка . Начальная вершина не имеет родителя, поэтому будем считать, что в нее входит фиктивная дуга стоимости 0.

1.8.2. АО*-алгоритм эвристического поиска на И-ИЛИ графе

Каждый преемник ИЛИ-вершины соответствует альтернативному дереву — кандидату в решение. АО*-алгоритм на каждом шаге будет расширять дерево с минимальной f-оценкой, вычисленной следующим образом:

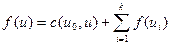— для И-вершины;

— для ИЛИ-вершины.

Рассмотрим эвристический поиск на примере модельного И-ИЛИ графа (рис. 23) с эвристиками всех вершин тождественно равными 0 (h(u)≡0 для всех u).

Рисунок 23. Модельный граф с эвристиками всех вершин тождественно равными нулю

Начнем поиск из начальной вершины а.

f(a) = 0 + h(a) = 0 (рис. 24):

Рисунок 24. Трассировка алгоритма. Шаг 1

Далее находим всех преемников а, вычисляем их f –оценки и пересчитываем f — оценку а (рис. 25):

f(b) = 1 + h(b) =1;

f(c) = 3 + h(c) = 3;

f(a) = 0 + min{f(b),f(c)} = min{1,3} = 1.

Рисунок 25. Трассировка алгоритма. Шаг 2

Дерево с корнем в b является минимальным, поэтому оно расширяется (рис. 26), его оценка пересчитывается и пересчитывается оценка вершины а:

f(d) = 1 + h(d) =1;

f(e) = 1 + h(e) =1;

f(b) = 1 + f(d) + f(e) =3.

Рисунок 26. Трассировка алгоритма. Шаг 3

f(b) ≤ f(c), поэтому продолжаем расширять дерево с корнем в b. При попытке расширить d обнаруживаем что d — целевая вершина, для e находим преемника h (рис. 27):

f(h) = 6 + h(h) =6;

f(e) = 1 + h(h) =1 + 6 =7;

f(b) = 1 + f(d) + f(e) = 1 + 1 + 7 = 9

Рисунок 27. Трассировка алгоритма. Шаг 4

Поиск не успел понять, что h — целевая вершина; стоимость дерева с корнем в b равна 9, поэтому происходит переключение на дерево с корнем в с, причем рост дерева с корнем в с ограничивается величиной 9: f(c) ≤ 9 (рис. 28):

f(f) = 2 + h(f) =2;

f(g) = 1 + h(g) =1;

f(c) = 3 + f(f) +f(g) = 3 + 2 + 1 =6;

Рисунок 28. Трассировка алгоритма. Шаг 5

f(b) ≤ 9, поэтому продолжаем расширять дерево с корнем в с (рис. 29). Обнаруживаем, что g — целевая вершина и для f находим двух преемников:

f(h) = 2 + h(h) = 2;

f(i) = 3 + h(i) = 3;

f(f) = 2 +min {2,3} = 4;

f(c) = 3 + f(f) + f(g) = 8

f(a) = 0 + f(c) = 8.

Рисунок 29. Трассировка алгоритма. Шаг 6

Штриховой линией обведено активное дерево поиска. Заметим, что вершина h включена в разные деревья поиска и имеет разные f оценки: 6 и 2. f(c)≤8≤9, поэтому продолжаем расширять дерево с корнем в c. При попытке расширить h обнаруживаем целевую вершину и получаем дерево решения. Так как все h(u) ≡ 0, то оценка вершины а — f(a) есть стоимость дерева решения.

1.8.3. Некоторые свойства АО*-алгоритма

Обозначим стоимость минимального дерева решения, связывающего вершину u с терминальными вершинами.

Если для всех u, то эвристический поиск построит минимальное дерево решения. Это условие для эвристики h можно заменить другим — условием монотонности эвристики h.

Пусть у вершины u имеется несколько связок, одна связка состоит из k потомков u₁,…, u_k. Если для каждой связки имеет место неравенство

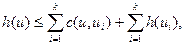
где с(u,u_i) — стоимость дуги от вершины u до потомка u_i, h(u_i) — эвристика вершины u_i, и для каждой терминальной вершины t h(t)≡0. Это условие аналогично условию монотонности для обычного графа пространства состояний:

т.е. эвристики вершин не меняются резко и согласованы со стоимостью дуг.

Дата добавления: 2015-06-27