Приклади розв’язання комбінаторних задач за допомогою леми Бернсайда

Задача про намиста

Задача.

Знайти кількість намист, що складаються з n бусинок двох кольорів. Намиста, що співпадають при повороті, вважаються однаковими.

Розв’язання

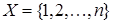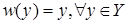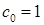Нехай множина відповідає номерам бусинок в намисті, а - множині можливих кольорів. Вагову функцію . В множині існує один елемент ваги нуль і один ваги один, тобто і .

Звідки слідує, що .

Нехай 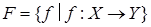- множина всіх функцій з в . Будь-яка функція задає деяке намисто, і навпаки, кожне намисто задається деякою функцією з 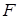. При цьому вага функції рівна кількості бусинок кольору 1, у відповідному намисті.

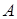На множині діє група поворотів , породжена циклічною перестановкою , яка визначається відношенням еквівалентності на 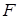. Тоді намиста співпадають при повороті будуть в точності відповідати еквівалентним функціям, і задача зводиться до підрахунку числа орбіт.

Цикловий індекс групи 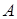рівний , де 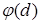- функція Ейлера, - НСД(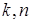); - дільник .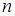

За теоремою Рефілдера-Пойа

Число орбіт ваги 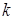(тобто різноманітних бусинок з кольором 1) дорівнює 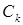коефіцієнту при 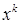в .

Тому загальне число орбіт (чи намист) дорівнює

.

У випадку для розфарбування намиста з 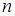бусинок, за допомогою 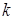кольорів, формула набуде такого вигляду:

.

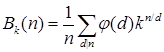Задача

Визначити кількість різних бус із 6 бусин, кожна з яких може бути розфарбована в один з трьох кольорів.

Розв’язання

Уточнимо умову задачі. Під різними бусами розуміють ті, що не можна співставити один з одним за допомогою повороту та осьової симетрії. Занумеруємо місця бусинок від 1 до 6, а кольорами – буквами 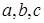. Тоді розфарбування – це співставлення конкретного кольору кожному із місць, тобто послідовність , де . Очевидно, що всього існує 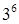таких розфарбувань. Зрозуміло, що не всі розфарбування відповідають різним бусам. Наприклад, розфарбування, має колір 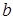, а інші – колір , суміщається поворотом з розфарбуванням, у якого друга бусина має колір 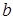, а всі інші мають колір .

На множині всіх розфарбувань діє група з поворотом та осьовою симетрією. Операція в цій групі – композиція, тобто послідовне виконання перетворень (композиція повороту і осьової симетрії рівносильна осьовій симетрії відносно іншої осі, а композиція двох симетрій відносно різних осей рівносильна повороту). Операція композиції є асоціативною, а нейтральним елементом є тотожне перетворення, оберненим рухом до осьової симетрії є сама осьова симетрія, а оберненим до повороту – є поворот, тільки в іншу сторону. Позначимо цю групу літерою .

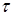Група діє на множині місць , тобто задано відображення з в симетричну групу . Позначимо через поворот, при якому переходимо на наступне місце (останнє в перше), а через - осьову симетрію відносно осі, що проходить через 6 і 1, 3 і 4. Випишемо перестановки в циклічній формі з , в якій переходить кожен з елементів групи .

Елемент
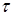
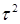
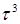
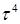
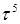
Перест.		(123456)	(135)(246)	(14)(25)(46)	(153)(264)	(654321)

Табл. 1.

Елемент
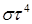
Перест.	(16)(25)(34)	(15)(24)	(14)(23)(56)	(13)(46)	(12)(36)(45)	(26)(35)

Табл. 2.

Далі ми будемо ототожнювати перетворення з відповідними їм перестановками. Тепер легко задати формулу дії елементів групи на множині :

Наприклад, колір другої бусинки після повороту 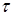, тобто повороту бус на 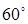співпадає з кольором першої бусинки до повороту (, тому ).

Нагадаємо, що розфарбування, що співпадають один з одним при перетвореннях, що відбуваються у групі , тобто задають однакові буси. В розфарбуваннях однакові буси задають тоді, коли вони лежать в одній орбіті під дією групи . Таким чином, задача полягає в тому, щоб визначити кількість орбіт дії на .

Для того, щоб скористатись лемою Бернсайда, потрібно визначити, скільки елементів множини залишається на місці кожного елементу з групи . Очевидно, що 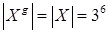. Так як поворот 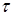сусідні елементи один в одного, то у розфарбуванні, не змінюються при цьому повороті, будь-які дві сусідні бусини такого розфарбування мають однаковий колір. Звідси слідує, що всі бусини такого розфарбування мають однаковий колір, .

В загальному ті бусини, елемент групи яких переставляється по циклу мають однаковий колір тоді і тільки тоді, коли елемент групи зберігає розфарбування. Тому кількість кольорів, яку потрібно обрати для отримання розфарбування, що зберігає елемент групи, рівна кількості незалежних циклів в перестановці, відповідаючи даному елементу. Для елементу 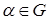позначимо це число . Так як за умовою бусини можна розфарбовувати у один з трьох кольорів, то можна обрати способами. Таким чином - це і є кількість розфарбувань, що не змінюються під дією елементу . Отримаємо:

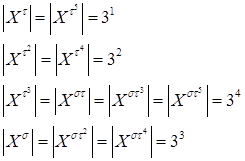
Використовуючи лему Бернсайда, знайдемо кількість бусин:

Відповідь: 56.

Формула Бернсайда може бути використана для обчислення незалежних від поворотів розфарбувань граней куба.

Нехай множина всіх 36 можливих розфарбувань граней куба в три кольори, а - група поворотів куба, що діє на . Два елементи належать до однієї орбіти, якщо один одержується з іншого за допомогою деякого повороту. Тож для обрахунку різних кубів треба обчислити кількість орбіт у множині під дією групи . Для цього визначимо кількість незмінних елементів для кожного з 24 поворотів і використаємо лему Бернсайда.

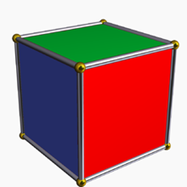
Рис.1 Куб з кольоровими гранями

одиничний елемент при кому усі 36 елементів залишаються незмінними

шість поворотів на 90 градусів навколо осей, що з'єднують центри протилежних граней, при кожному 33 елементів залишаються незмінними

три повороти на 180 градусів навколо осей, що з'єднують центри протилежних граней, при кожному 34 елементів залишаються незмінними

вісім поворотів на 120 градусів навколо осей, що з'єднують протилежні вершини, при кожному 32 елементів залишаються незмінними

шість поворотів на 180 градусів навколо осей, що з'єднують центри протилежних ребер, при кожному 33 елементів залишаються незмінними

Тому згідно леми Бернсайда:

Отже, загальна кількість різних з урахуванням поворотів кубів, грані яких розфарбовані в три кольори, рівна 57. Загалом, якщо грані розфарбовані в n кольорів, то справедлива формула:

Висновки

Хоч теорія груп достатньо молода галузь математики, але завдяки титанічним зусиллям багатьох поколінь математиків (Ж-Л. Лагранжа, Е. Галуа, Л. Ейлера, Н. Абеля та ін.) знайшла своє застосування у інших областях «цариці наук». В даній роботі ми розглянули застосування теорії груп при розв’язуванні комбінаторних задач, а точніше при розв’язуванні задачі про знаходження кількості різних намист, що складаються з 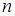намистин, що пофарбовані в 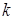кольорів.

Опорним фактом для розв’язування задачі «про намиста» є твердження, яке відоме в комбінаториці під назвою «лема Бернсайда». Тому одним із завдань даної роботи було сформулювати та довести це важливе твердження. Виконання цього завдання передбачало використання теоретичного матеріалу з теорії груп, який ми висвітлили в першій половині роботи.

Перш ніж розв’язати задачу про намиста було сформулювано та довено теорему Рефілдера-Пойа, на основі якої ґрунтується розв’язання. В свою чергу доведення цієї теореми ґрунтується на основі леми Бернсайда. Потім, використовуючи теорему Рефілдера-Пойа було успішно розв’язано задачу про намиста. Далі в роботі було продемонстровано декілька прикладів застосування леми Бернсайда при розв’язуванні комбінаторних задач.

За результатами проведеного курсового дослідження на тему «Лема Бернсайда і задача про намиста» можна зробити висновок, що комбінаторні задачі про кількість об'єктів, що не суміщаються один з одним певними перетвореннями, які розв’язуються за допомогою леми Бернсайда, є цікавим важливим застосуванням теорії груп.

Дата добавления: 2015-06-27