
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математические модели
|
|
|
|
1. Построение математической модели. Исследование экономических процессов обычно начинается с их моделирования, т.е. определения математических соотношений, которым эти процессы подчиняются. При этом необходимо:
- определить переменные данной задачи, т.е. величины, которые по полностью характеризуют данный экономический процесс (все они по смыслу – неотрицательные величины);
- установить, каким ограничениям удовлетворяют переменные (в соответствии с условиями задачи);
- построить целевую функцию (функцию выбранных переменных, экстремум которой – максимум или минимум – необходимо найти).
Пример 1. На фабрике производится продукция двух типов. Для производства единицы продукции первого типа требуются 2 часа работы станка A, 1 час работы станка B и 1 час на завершающие операции. Для производства единицы продукции второго типа требуются 1 час работы станка A, 1 час работы станка B и 3 часа на завершающие операции. В течение недели станок A может работать не более 70 часов, станок B не более 40 часов, и на завершающие операции выделяется не более 90 часов. Доход от продажи единицы продукции первого типа составляет 4 у.е., от продажи единицы продукции второго типа 6 у.е. Сколько продукции первого и второго типа следует производить за неделю, чтобы доход был максимальным?
Решение. Очевидно, что в качестве переменных x и y следует взять количество (в единицах) продукции первого и второго (соответственно) типа. При этом 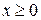 ,
, 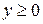 , а целевая функция (доход, который должен быть максимальным) имеет вид
, а целевая функция (доход, который должен быть максимальным) имеет вид 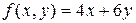 и
и 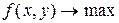 . Теперь обратим внимание на условия, диктующие ограничения на переменные. Для производства обоих видов продукции станок A должен работать 2x+1y часов, станок В 1x+1y часов и на завершающие операции требуется 1x+3y часов. Учитываем указанные в задаче возможности работы станков и окончательно получаем:
. Теперь обратим внимание на условия, диктующие ограничения на переменные. Для производства обоих видов продукции станок A должен работать 2x+1y часов, станок В 1x+1y часов и на завершающие операции требуется 1x+3y часов. Учитываем указанные в задаче возможности работы станков и окончательно получаем:

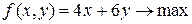
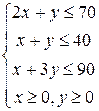
|
|
|
|
|
Дата добавления: 2015-06-27; Просмотров: 225; Нарушение авторских прав?; Мы поможем в написании вашей работы!