Момент инерции простейших твердых тел и плоских фигур

1. Момент инерции однородного тонкого круглого кольца радиуса 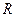и массы .

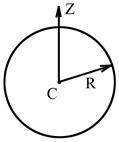
Рис. 17

Так как все точки кольца находятся от оси 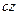на одинаковом расстоянии (рис.17), то по формуле (6.1) 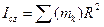. Так как , то

2. Момент инерции однородного тонкого стержня длины и массы .

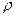Пусть стержень длины имеет постоянное малое сечение и плотность . Тогда масса стержня .

Разобьем данный стержень на множество элементарных частей длиной 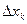(рис. 18). Их масса равна .

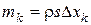Рис. 18

Вычислим момент инерции стержня относительно оси :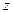

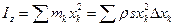
Переходя в этом равенстве к пределу, получим определенный интеграл:

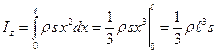
Так как 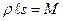- масса стержня, то 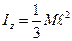. Если ось будет проходить через центр масс стержня то по теореме Гюйгенса . Так как у нас будет , то 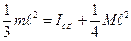, тогда .

3. Момент инерции однородной круглой пластинки малой толщины радиуса 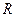и массы .

Рис. 19

Пусть пластинка имеет весьма малую толщину 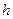и плотность 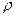. Тогда масса пластинки .

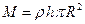Разобьем пластину на множество элементарных колец радиусом 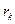и шириной 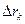. Масса кольца 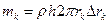. По формулам (6.2) будем иметь 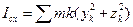, 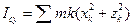. Так как - весьма малая величина, то пренебрегая будем иметь , 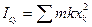. Момент инерции пластинки относительно оси 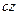, 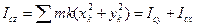. Так как пластинка симметрична относительно 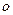и , и , 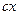то и .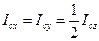

Так как , то 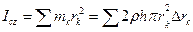. Переходя к пределу получим определенный интеграл: . Так как 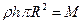- масса пластинки, то.

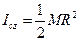
(6.3)

Тогда .

4. Момент инерции однородной тонной прямоугольной пластинки размерами 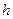, и массы (рис. 20).

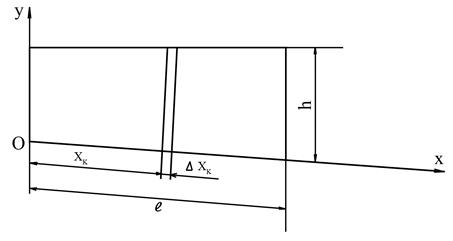
Рис. 20

Пусть плотность пластинки 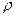. Тогда масса пластинки .

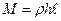Разобьем пластинку на множество элементарных полосок шириной 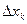. Их масса равна .

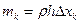Найдем момент инерции элементарной полоски относительно оси 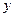: . Тогда момент инерции пластинки .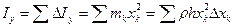

Переходя к пределу получим: . Так как , то .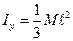

Аналогично рассуждая, получим .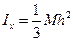

5. Момент инерции однородного круглого цилиндра радиуса 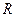, высоты и массы . Пусть плотность цилиндра 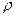. Тогда масса цилиндра 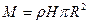. Разобьем цилиндр на множество элементарных пластинок толщиной 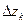. Масса пластинки (рис. 21).

Рис. 21

Момент инерции цилиндра относительно оси 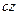определим, как сумму моментов инерции элементарных пластинок

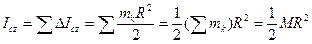
По теореме Гюйгенса 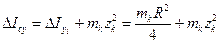. Тогда

. Перейдем к пределу. Тогда

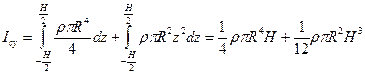. Так как 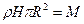- масса цилиндра, то 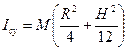. Таким образом, 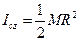. Так цилиндр симметричен относительно осей 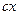и , то .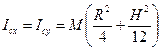

6. Момент инерции полого цилиндра.

Момент инерции полого цилиндра с внешним радиусом 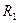и с внутренним радиусом 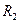(рис. 22) относительно оси 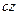можно определить как разность моментов инерции сплошных цилиндров радиусам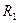и и .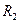

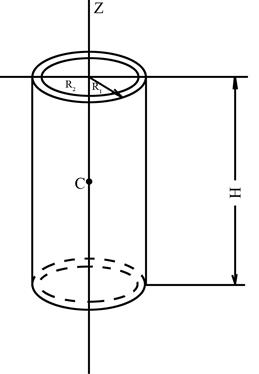
Рис. 22

, если плотность сплошных цилиндров 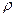, то их масса ,

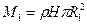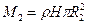. Тогда . Масса полого цилиндра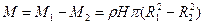

Окончательно: .

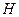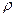7. Момент инерции однородного круглого конца. Допустим, что конус имеет высоту , радиус основания и плотность . Тогда масса конуса .

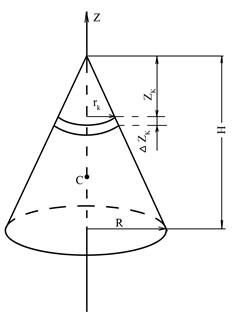
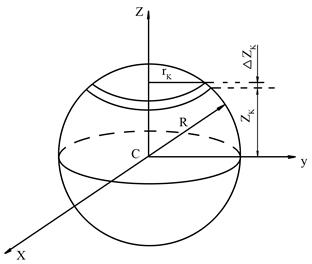
а) б)

Рис. 23

Для определения разобьем конус на множество элементарных пластинок толщиной (рис. 23, а). Масса пластинки радиуса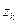

.

Так как 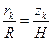, то .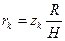

Момент инерции элементарной пластинки .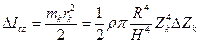

Момент инерции конуса получим, суммируя моменты инерции элементарных пластинок; переходя к пределу суммы, имеем

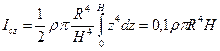
После подстановки 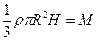, получим .

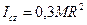8. Момент инерции однородного шара.

Разобьем шар на множество элементарных пластинок толщиной масса пластинки радиусом (рис. 23,б).

.

Момент инерции элементарной пластинки относительно оси 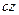определяем по формуле (6.3) с последующей подстановкой: ;

.

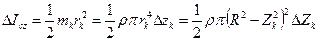Момент инерции шара относительно оси 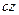, получаем суммируя момент инерции элементарных пластинок, и переходя к пределу суммы:

После подстановки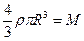

Так как оси , , 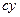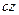проведены по диаметрам шара, то .

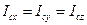Дата добавления: 2015-06-27