Однородные системы линейных уравнений

Ранг матрицы. Базисный минор матрицы.

Минором матрицы порядка s называется определитель матрицы, образованный из элементов исходной матрицы, находящихся на пересечении каких-либо выбранных s строк и s столбцов.

Рангом матрицы А называется наибольший порядок отличных от нуля миноров этой матрицы. Обозначается: r(A), rang (A), r_A.

Базисным минором называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.

Элементарными преобразованиями матрицы называются следующие:

1) перестановка строк (столбцов);

2) умножение строки (столбца) на число, отличное от нуля;

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на некоторое число

Теорема. Элементарные преобразования матрицы не меняют её ранга.

Используя элементарные преобразования, матрицу А можно привести к ступенчатому виду:

,

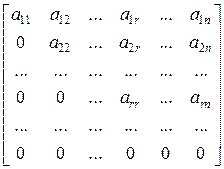где a₁₁, a_22, …, a_rr отличны от нуля.

Ранг полученной матрицы равен r.

Пример 1. Найти ранг матрицы 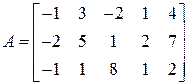. Указать какой-либо базисный минор.

Решение. С помощью элементарных преобразований приведём матрицу к ступенчатому виду:

.

Т.к. минор , а все миноры третьего порядка равны нулю, то ранг матрицы равен 2.

----------------------------------------------------------------------------------------------------------------

Однородные системы линейных уравнений. Стр. 1

Система линейных уравнений называется однородной, если её правая часть состоит только из нулей.

Однородная система всегда совместна, т.к. существует тривиальное решение .

Теорема. Система линейных однородных уравнений имеет ненулевое решение тогда и только тогда, когда ранг её матрицы меньше числа переменных, т.е. rang A<n.

Неизвестные, коэффициенты около которых входят в базисный минор, называются базисными, а все остальные – свободными (параметрическими).

Базисные неизвестные выражаются через свободные, которым придаются значения произвольных параметров. Таким образом получается общее решение системы.

Если выбрать n-r решений исходной системы следующим образом: одно из значений свободных переменных полагается равным 1, а остальные – равными 0, то полученные решения образуют нормальную фундаментальную систему решений.

Пример 2. Найти общее решение однородной СЛУ и выписать фундаментальную систему решений:

Решение. Приведём матрицу системы к ступенчатому виду:

Ранг данной матрицы равен 3.Следовательно, имеем 5-3=2 свободных переменных.

Составим систему уравнений, соответствующую полученной матрице:

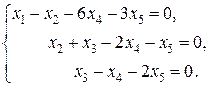
Пусть свободными переменными будут и . Тогда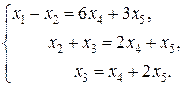

----------------------------------------------------------------------------------------------------------------

Однородные системы линейных уравнений. Стр. 2

Придадим свободным переменным значения параметров и выразим остальные переменные через эти параметры:

Общее решение:

Определим фундаментальную систему решений:

Значит, фундаментальная система решений имеет вид: {(7; 1; 1; 1; 0); (2; -1; 2; 0; 1)}

Дата добавления: 2015-06-27