Построение минимаксных решающих правил (решение статистической игры)

Непосредственное построение минимаксных решающих правил по определению, приведенному в п. 3.1, обычно бывает затруднительным. Поэтому используют два основных подхода к решению статистической игры.

1. Первый подход к отысканию минимаксных решающих правил основан на свойствах наименее благоприятного априорного распределения.

Теорема 1. Если статистическая игра имеет значение и если 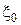есть наименее благоприятное априорное распределение состояний природы , то каждое минимаксное решающее правило 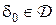будет байесовским относительно .

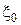Если множество априорных распределений 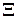имеет достаточно простую структуру - например. при имеем

,

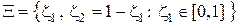то нетрудно найти наименее благоприятное априорное распределение. используя вогнутость минимального байесовского риска .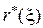

Часто можно сделать некоторое разумное предположение относительно 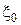, найти соответствующее байесовское решающее правило 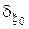, а затем убедиться, является ли оно минимаксным, пользуясь следующим утверждением.

Теорема 2. Если решающее правило 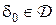является байесовским относительно некоторого априорного распределения 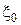и для любого имеет место неравенство 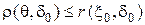, то статистическая игра имеет значение 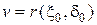, 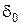есть минимаксное решающее правило, а 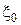- наименее благоприятное априорное распределение.

Иногда удобно пользоваться более общей формулировкой этой теоремы.

Теорема 2а. Пусть в статистической игре 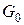распределения вероятностей 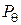на принадлежат некоторому подсемейству 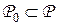общего семейства вероятностных мер 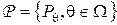и пусть для этой игры имеется минимаксное решающее правило 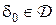, а 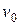- значение игры. Тогда, если 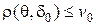при любом 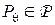, то решающее правило 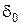будет минимаксным и для более общей статистической игры 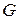, в которой .

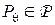Если наименее благоприятное априорное распределение 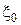не существует, то может быть предпринята попытка построить соответствующую максимизирующую последовательность априорных распределений.

Теорема 3. Пусть 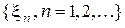- последовательность априорных распределений на 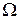и 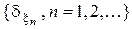- последовательность соответствующих байесовских решающих правил с байесовскими рисками 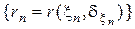. Если 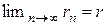и существует такое решающее правило 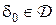, что для любого выполняется неравенство , то 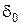есть минимаксное решающее правило, а 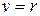есть значение игры.

2. Второй подход к отысканию минимаксных решающих правил основан на понятии уравнивающего решающего правила, то есть такого решающего правила 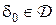, для которого 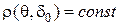при любом .

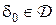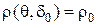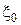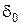Теорема 4. Если решающее правило является уравнивающим с риском и если оно является байесовским относительно некоторого априорного распределения , то есть минимаксное решающее правило, а 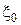- наименее благоприятное априорное распределение, причём значение игры равно .

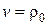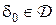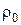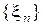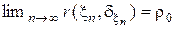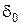Теорема 5. Если решающее правило является уравнивающим с риском и если существует последовательность априорных распределений такая, что , то есть минимаксное решающее правило.

Пример. Вероятность успеха 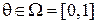в распределении Бернулли 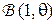неизвестна. Требуется выбрать решение 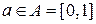на основании одного наблюдения случайной величины 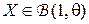при квадратичной функции потерь 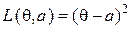. Соответствующая статистическая игра может служить, например. математической моделью следующей прикладной задачи: оценить вероятность 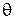безотказной работы в течение гарантийного срока для некоторых изделий, выпускаемых предприятием, называя оценку 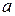на основании испытания одного образца изделия (с исходом 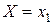- безотказная работа или 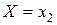- отказ) при потере, пропорциональной квадрату ошибки оценивания.

Таким образом, мы имеем 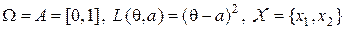, 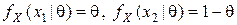. Выпуклость функции потерь позволяет сразу исключит рандомизацию (см. п. 5.1). Рассмотрим некоторое нерандомизированное решающее правило 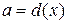. Здесь любое 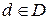можно представить точкой 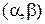в единичном квадрате 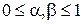в том смысле, что 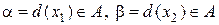. Непосредственный выбор наименее благоприятного априорного распределения 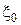на 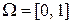затруднителен. Поэтому будем искать среди 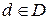уравнивающее решающее правило. Функция риска имеет вид:

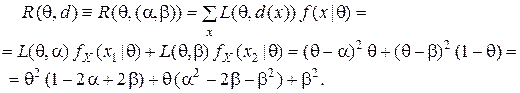
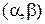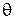Если решающее правило является уравнивающим, то его риск не зависит от и коэффициенты при и 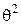в выражении для 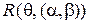должны быть равны нулю:

.

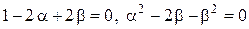Решая эту систему, находим единственное уравнивающее решающее правило 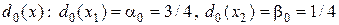. Оно имеет постоянный риск, равный .

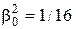В силу Теоремы 4 это решающее правило будет минимаксным, если оно является байесовским относительно некоторого априорного распределения 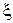. Для любого априорного распределения 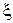на 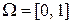, имеющего первые два момента и 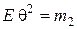, получим байесовский риск произвольного решающего правила :

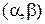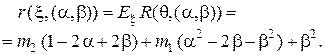
Байесовское решающее правило 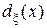относительно 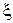будет описываться точкой 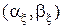, минимизирующей 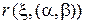. Значения 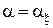и 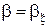найдём из системы уравнений

.

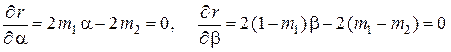Таким образом, 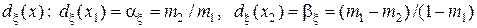. Уравнивающее решающее правило будет байесовским относительно 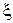при 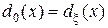. Для этого необходимо и достаточно, чтобы , .

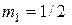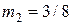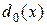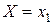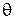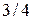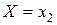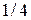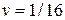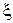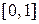Итак, минимаксное решающее правило в нашей задаче состоит в том, чтобы при оценивать как , а при - как . Значение игры равно и любое априорное распределение на с 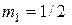, 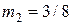является наименее благоприятным.

Дата добавления: 2015-06-27