Алгоритм Дейкстри 3 страница

		-
табл. 10

		-
табл.11

Оцінюємо тепер нулі в наведеній матриці C [(1,2), (3,1)] нуль з максимальною оцінкою 3 знаходиться в клітці (6,5). Негативний варіант має оцінку 38 + 3 = 41. Для отримання оцінки позитивного варіанта прибираємо сходинку 6 і стовпець 5, ставимо заборона у клітину (5,6), див. Табл. 10. Ця матриця непріводімим. Отже, оцінка позитивного варіанта не збільшується (рис.8).

Оцінюючи нулі в матриці на табл. 10, отримуємо розгалуження за вибором ребра (2,6), негативний варіант отримує оцінку 36 + 3 = 39, а для отримання оцінки позитивного варіанта викреслюємо другий рядок і шостий стовпець, одержуючи матрицю на табл. 11.

У матрицю треба додати заборона у клітину (5,3), бо вже побудований фрагмент туру [3,1,2,6,5] і треба заборонити передчасний повернення (5,3). Тепер, коли залишилася матриця 2х2 із заборонами по діагоналі, добудовуємо тур ребрами (4,3) і (5,4). Ми не даремно гілкувалися, по позитивним варіантів. Зараз отриманий тур: 1 → 2 → 6 → 5 → 4 → 3 → 1 вартістю в 36. При досягненні низу по дереву перебору клас турів звузився до одного туру, а оцінка знизу перетворилася в точну вартість.

Отже, всі класи, що мають оцінку 36 і вище, кращого туру не містять. Тому відповідні вершини викреслюються. Викреслюються також вершини, обидва нащадка якої викреслені. Ми колосально скоротили повний перебір. Залишилося перевірити, чи не містить кращого туру клас, відповідний матриці С [Not (1,2)], тобто наведеній матриці С із забороною в клітці 1,2, наведеної на 1 по стовпцю (що дало оцінку 34 + 1 = 35). Оцінка нулів дає 3 для нуля в клітці (1,3), так що оцінка негативного варіанту 35 + 3 перевершує вартість вже отриманого туру 36 і негативний варіант відсікається.

Для отримання оцінки позитивного варіанта виключаємо з матриці перший рядок і третій стовпець, ставимо заборона (3,1) і отримуємо матрицю. Ця матриця наводиться по четвертому рядку на 1, оцінка класу сягає 36 і гурток закреслюється. Оскільки у вершини «все» вбиті обидва нащадка, вона убивається теж. Вершин не залишилося, перебір закінчено. Ми отримали той же мінімальний тур, який показаний підкресленням на табл. 2.

Задовільних теоретичних оцінок швидкодії алгоритму Літтла та споріднених алгоритмів немає, але практика показує, що на сучасних ЕОМ вони часто дозволяють вирішити ЗК з n = 100. Це величезний прогрес у порівнянні з повним перебором. Крім того, алгоритми типу гілок і меж є, якщо немає можливості доводити їх до кінця, ефективними евристичними процедурами.

Одним з варіантів вирішення ЗК є варіант знаходження найкоротшої ланцюга, що містить всі міста. Потім отримана ланцюг доповнюється початковим містом - виходить шуканий тур.

Можна запропонувати багато процедур вирішення цього завдання, наприклад, фізичне моделювання. На плоскій дошці малюється карта місцевості, в міста, що лежать на розвилці доріг, забиваються цвяхи, на кожен цвях надівається кільце, дороги укладаються мотузками, які прив'язуються до відповідних кілець. Щоб знайти найкоротша відстань між i і k, потрібно взяти I в одну руку і k в іншу і розтягнути. Ті мотузки, які натягнуться і не дадуть розводити руки ширше і утворюють найкоротший шлях між i і k. Проте математична процедура, яка Промоделюйте цю фізичну, виглядає дуже складно. Відомі алгоритми простіше. Один з них - алгоритм Дейкстри, запропонований Дейкстрой ще в 1959р. Цей алгоритм вирішує загальну задачу:

В орієнтованої, неориентированной або змішаної (т. Е. Такий, де частина доріг має односторонній рух) мережі знайти найкоротший шлях між двома заданими вершинами.

Алгоритм використовує три масиву з n (= числу вершин мережі) чисел кожен. Перший масив a містить мітки з двома значеннями: 0 (вершина ще не розглянута) та 1 (вершина вже розглянута); другий масив b містить відстані - поточні найкоротші відстані від vi до відповідної вершини; третій масив c містить номери вершин - k-й елемент ck є номер передостанній вершини на поточному найкоротшому шляху з vi в vk. Матриця відстаней Dik задає довжини дуг dik; якщо такий дуги немає, то dik присвоюється велика кількість Б, рівне «машинної нескінченності».

Тепер можна описати:

алгоритм Дейкстри

1 (ініціалізація).

У циклі від одного до n заповнити нулями масив а; заповнити числом i масив з: перенести i-тую рядок матриці D в масив b;

a [i]: = 1; c [i]: = 0; {i-номер стартовою вершини}

2 (загальний крок).

Знайти мінімум серед невідмічених (т. Е. Тих k, для яких a [k] = 0); нехай мінімум досягається на індексі j, т. е. bjbk; a [j]: = 1;

			∞	∞	∞	∞	∞
			∞		∞	∞
				∞	∞	∞	∞
∞	∞			∞		∞	∞
∞		∞	∞				∞
∞	∞	∞					∞
∞	∞	∞	∞
∞		∞	∞	∞	∞
табл. 12

якщо bk> bj + djk то (bk: = bj + djk; ck: = j) {Умова означає, що шлях vi..vk довший, ніж шлях vi..vj, vk. Якщо все a [k] відзначені, то довжина шляху vi..vk дорівнює b [k]. Тепер треба перерахувати вершини, що входять до найкоротший шлях}

3 (видача відповіді).

{Шлях vi..vk видається в зворотному порядку наступною процедурою:}

3.1. z: = c [k];

3.2. Видати z;

3.3. z: = c [z]; Якщо z = 0, то кінець, інакше перейти до 3.2.

Для виконання алгоритму потрібно n раз переглянути масив b з n елементів, т. Е. Алгоритм Дейкстри має квадратичну складність. Проілюструємо роботу алгоритму Дейкстри чисельним прикладом (для більшої складності, вважаємо, що деякі міста (вершини) i, j пов'язані між собою, т. Е. D [i, j] = ∞). Нехай, наприклад, i = 3. Потрібно знайти найкоротші шляхи з вершини 3. Вміст масивів a, b, c після виконання першого пункту показано на табл. 12:

a
b					∞	∞	∞	∞
c
табл. 13

Очевидно, вміст таблиці змінюється по мірі виконання загального кроку. Це видно з наступної таблиці:

min bk=12	a
b					∞	∞	∞	∞
c
min bk=18	a
b					∞		∞	∞
c
min bk=25	a
b							∞
c
min bk=38	a
b
c
min bk=47	a
b
c
min bk=60	a
b
c

Таким чином, для вирішення ЗК потрібно n раз застосувати алгоритм Дейкстри наступним чином.

Візьмемо довільну пару вершин

j, k. Виключимо безпосереднє ребро C [j, k]. За допомогою алгоритму Дейкстри знайдемо найкоротша відстань між містами j..k. Нехай це відстань включає деякий місто m. Маємо частина туру j, m, k. Тепер для кожної пари сусідніх міст (в даному прикладі - для j, m і m, k) видалимо відповідне ребро і знайдемо найкоротша відстань. При цьому в найкоротша відстань не повинен входити вже використаний місто.

Далі аналогічно знаходимо найкоротша відстань між парами вершин алгоритмом Дейкстри, до тих пір, поки всі вершини не будуть задіяні. З'єднаємо останню вершину з першої і отримаємо тур. Найчастіше це останнє ребро виявляється дуже великим, і тур виходить з похибкою, проте алгоритм Дейкстри можна віднести до наближених алгоритмам.

1.3.5. Мій метод (метод Ярощука) рішення задачі комівояжера

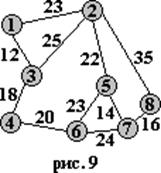
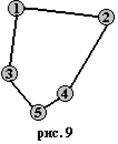
Розглянемо рис. 9-10 і спробуємо знайти в них найкоротші тури. Очевидно, що найкоротший тур не повинен містити пересічних ребер (в іншому випадку, помінявши вершини при пересічних ребрах місцями, отримаємо більш короткий тур). У першому випадку найкоротшим є тур 1-2-4-5-3-1, а в другому - тур 1-2-3-4-5-1. Аналізуючи безліч інших аналогічних розташувань п'яти і більше міст, можна зробити наступне загальне припущення:

1. Якщо можна побудувати опуклий багатокутник, по периметру якого лежать всі міста, то такий опуклий багатокутник є найкоротшим туром.

Однак не завжди можна побудувати опуклий багатокутник, по периметру якого лежали б всі міста. Велика ймовірність того, що деякі міста не увійдуть до опуклий багатокутник. Такі міста будемо називати «центральними». Так як побудувати опуклий багатокутник досить легко, то завдання зводиться до того, щоб включити в тур у вигляді опуклого багатокутника всі центральні міста з мінімальними втратами. Нехай є масив T [n + 1], який містить в собі номери міст по порядку, які повинен відвідати комівояжер, т. Е. Спочатку комівояжер повинен відвідати місто T [1], потім T [2], потім T [3] і т. д,, причому T [n + 1] = T [1] (комівояжер повинен повернутися в початковий місто). Тоді, якщо виконується рівність i∈ [1,2..n]; C [T [i], p] + C [p, T [i + 1]] - C [T [I], T [i + 1]] = min, то центральний місто з номером p потрібно включити в тур між містами T [i] і T [i + 1]. Виконавши цю операцію для всіх центральних міст, в результаті отримаємо найкоротший тур. Даний алгоритм можна реалізувати на мові Паскаль і перевірити вірність припущення 1. Для задачі, вирішеною нами методом гілок і меж, мій алгоритм дає правильне рішення.

Спробуємо вирішити даним алгоритмом ЗК для восьми міст. Нехай маємо вісім міст, розташування яких показано на рис. 11. Матриця відстаней наведена поруч на табл. 13. Проміжні побудови найкоротшого туру показані пунктирними лініями, цифри - порядок видалення ребер. Таким чином, маємо для даного випадку найкоротший тур 1-3-7-5-4-8-6-2-1. Довжина цього туру: D = 6 + 7 + 5 + 2 + 6 + 5 + 13 + 13 = 57. Цей результат є правильним, т. К. Алгоритм лексичного перебору, який ніколи не помиляється, дає точно такий же тур. (Слід також зазначити, що жодній алгоритм для цього випадку помиляється всього на 1 і дає тур 1-3-4-5-7-8-6-2-1 довжиною в 58).

табл. 13

Одним з можливих недоліків такого алгоритму є необхідність знати не матрицю відстаней, а координати кожного міста на площині. Якщо нам відома матриця відстаней між містами, але невідомі їх координати, то для їх знаходження потрібно буде вирішити n систем квадратних рівнянь з n невідомими для кожної координати. Вже для 6 міст це зробити дуже складно. Якщо ж, навпаки, є координати всіх міст, але немає матриці відстаней між ними, то створити цю матрицю нескладно. Це можна легко зробити в умі для 5-6 міст. Для більшої кількості міст можна скористатися можливостями комп'ютера, в той час як промоделювати рішення системи квадратних рівнянь на комп'ютері досить складно.

На основі вищевикладеного можна зробити висновок, що мій алгоритм, поряд з дерев'яним алгоритмом і алгоритмом Дейкстри, можна віднести до наближених (хоча за цим алгоритмом жодного разу не було помічено видачі неправильного варіанту).

1.4 Аналіз методів рішення задачі комівояжера

Для підведення підсумків у вивченні методів вирішення ЗК протестуємо найбільш оптимальні алгоритми на комп'ютері за наступними показниками: кількість міст, час обробки, ймовірність неправильної відповіді. Дані занесемо в таблицю.

Алгоритм лексического перебора
Кол-во городов	Время обработки, c	Вероятность неправильного ответа, %	Тип алгоритма
			точный
	12000=3ч.20мин
	-*
	-*
Метод ветвей и границ
	~0		точный
	~0.0001
	1.2
Мой алгоритм решения ЗК
	0.001		приближенный
	2.5

* - ЗК з такою кількістю міст методом лексичного перебору сучасний комп'ютер не зміг би вирішити навіть за весь час існування Всесвіту.

Як бачимо за результатами цієї таблиці, алгоритм лексичного перебору можна застосовувати лише у випадку з кількістю міст 5..12. Метод гілок і меж, поряд з моїм методом, можна застосовувати завжди. Хоча мій метод я відніс до наближених алгоритмам, він фактично є точним, так як довести зворотне ще не вдалося.

1.5 Практичне застосування задачі комівояжера

Крім очевидного застосування ЗК на практиці, існує ще ряд завдань, приводяться до вирішення ЗК.

Завдання про виробництві фарб. Є виробнича лінія для виробництва n фарб різного кольору; позначимо ці фарби номерами 1,2... n. Всю виробничу лінію будемо вважати одним процесором.. Будемо вважати також, що одноразово процесор виробляє тільки одну фарбу, тому фарби потрібно виробляти в деякому порядку Оскільки виробництво циклічне, то фарби треба виробляти в циклічному порядку  = (j1, j2,.., jn, j1). Після закінчення провадження фарби i і перед початком виробництва фарби j треба відмити обладнання від фарби i. Для цього потрібен час C [i, j]. Очевидно, що C [i, j] залежить як від i, так і від j, і що, взагалі кажучи, C [i, j] ≠ C [j, i]. При деякому вибраному порядку доведеться на цикл виробництва фарб витратити час.

Таким чином, ЗК і завдання щодо мінімізації часу переналагодження - це просто одна задача, тільки варіанти її описані різними словами.

Завдання про діропробивні преси. Діропробивний прес справляє велике число однакових панелей - металевих листів, в яких послідовно по одному пробиваються отвори різної форми і величини. Схематично прес можна представити у вигляді столу, що рухається незалежно за координатами x, y, і обертового над столом диска, по периметру якого розташовані диропробивні інструменти різної форми і величини. Кожен інструмент є у одному примірнику. Диск може обертатися однаково в двох напрямках (координата обертання z). Мається власне прес, який натискає на підвішений під нього інструмент тоді, коли під інструмент підведена потрібна точка листа.

Операція пробивки j-того отвори характеризується четвіркою чисел (xj, yj, zj, tj),, де xj, yj- координати потрібного положення столу, zj - координата потрібного положення диска і tj - час пробивки j-того отвори.

Виробництво панелей носить циклічний характер: на початку і наприкінці обробки кожного аркуша стіл повинен знаходитися в положеннях (x0, y0) диск в положенні z0 причому в цьому положенні слив не пробивається. Це початковий стан системи можна вважати пробивкой фіктивного нульового отвори. З параметрами (x0, y0, z0,0).

Щоб пробити j-тое отвір безпосередньо після i-того необхідно зробити наступні дії:

1. Перемістити стіл по осі x з положення xi в положення xj, витрачаючи при цьому час t (x) (| xi-xj |) = ti, j (x)

Проробити те ж саме по осі y, витративши час ti, j (y)

Повернути головку по найкоротшій з двох дуг з положення zi в положення zj, витративши час ti, j (z).

Пробити j-тое отвір, витративши час tj.

Конкретний вид функцій t (x), t (y), t (z) залежить від механічних властивостей преса і досить громіздкий. Явно виписувати ці функції немає необхідності

Дії 1-3 (переналагодження з i-того отвори j-тое) відбувається одночасно, і пробивка відбувається негайно після завершення самого тривалого з цих дій. Тому

С [i, j] = max (t (x), t (y), t (z))

Тепер, як і в попередньому випадку, завдання складання оптимальної програми для діропробивні преси зводиться до ЗК (тут - симетричною).

РОЗДІЛ 2
НАЗВА РОЗДІЛУ

2.1 Назва підрозділу

Текст підрозділу 2.1 Предметом дослідження є маркетингова політика розподілу даного підприємства.

…. залежність виражається формулою: (Примітка. Формули, що йдуть одна за одною і не розділені текстом, відокремлюють комою і між ними відсутні вільні рядки, після останньої формули ставиться крапка. Номер формули зазначають на рівні формули у дужках у крайньому правому положенні на рядку. Вище і нижче кожної формули повинно бути не менше одного рядка.)

Р = Оп + Т-Ок, (2.1)

де Р - обсяг виручки, від реалізації товарної продукції;

Т - обсяг товарної продукції;

Оп і Ок — перехідні залишки нереалізованої продукції на початок і на кінець звітного періоду.

Дата добавления: 2015-06-28