
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Каноническое уравнение гиперболы
|
|
|
|
Определение 12. Гиперболй называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек  и
и  этой плоскости, называемых фокусами, есть величина постоянная (И, П, стр. 146).
этой плоскости, называемых фокусами, есть величина постоянная (И, П, стр. 146).
Определение 13. Указанные выше точки  и
и  называются фокусами гиперболы (А, стр.75)
называются фокусами гиперболы (А, стр.75)
Нетрудно заметить, что если фокусы совпадают и указанная в определении гиперболы постоянная равна нулю, то любая точка плоскости удовлетворяет этому условию; если же указанная постоянная не равна нулю, то таких точек не существует точек (И, П, стр. 146). Поэтому далее мы предполагаем, что точки  и
и  не совпадают.
не совпадают.
Определение 14. Середина отрезка 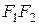 , соединяющего фокусы, называется центром гиперболы. (А, стр. 75).
, соединяющего фокусы, называется центром гиперболы. (А, стр. 75).
Определение 15. Прямая, на которой лежат фокусы гиперболы,называется фокальной или первой осью гиперболы (А, стр. 75 - 76).
Определение 16. Прямая, проходящая через центр гиперболы, перпендикулярно к фокальной оси, называется второй осью гиперболы (А, стр. 76).
Определение 17. Расстояние между фокусами  и
и  называется фокусным расстоянием (А, стр. 76).
называется фокусным расстоянием (А, стр. 76).
Для вывода канонического уравнения гиперболы декартову прямоугольную систему координат Оху выбирают аналогично тому, как это было сделано при выводе уравнения эллипса. Начало координат О размещают в центре гиперболы, т.е. на середине отрезка 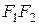 ,в качестве оси Ох выбирают фокальнуюось (рисунок 6). Система координат такого вида называется канонической системой (для данной гиперболы)
,в качестве оси Ох выбирают фокальнуюось (рисунок 6). Система координат такого вида называется канонической системой (для данной гиперболы)

Рисунок 6 – Каноническая система
координат
Пусть длина отрезка 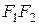 равна
равна  ,
,  . Тогда, в выбранной системе координат, координаты точек
. Тогда, в выбранной системе координат, координаты точек  и
и  -
-  и
и 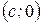 , соответственно (рисунок 7). Как и для эллипса, фокус
, соответственно (рисунок 7). Как и для эллипса, фокус  в этом случае условно называют левым фокусом, а фокус
в этом случае условно называют левым фокусом, а фокус  - правым фокусом.
- правым фокусом.
|
|
|
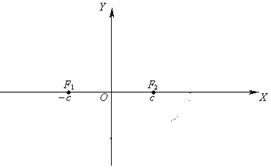

 Рисунок 7 – Координаты фокусов Рисунок 8 – Отрезки расстояний
Рисунок 7 – Координаты фокусов Рисунок 8 – Отрезки расстояний
Пусть абсолютная величина разности расстояний от точек гиперболы (исследуемого геометрического множества точек) до фокусов  и
и  равна
равна  . Очевидно, что
. Очевидно, что  (А, стр. 76). Поскольку случай
(А, стр. 76). Поскольку случай 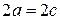 приводит к ситуации, когда точка располагается на фокальной оси вне отрезка
приводит к ситуации, когда точка располагается на фокальной оси вне отрезка 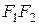 и гипербола вырождается в два луча (И.П,, СТР, 146, А, стр. 76), то далее ограничиваемся случаем
и гипербола вырождается в два луча (И.П,, СТР, 146, А, стр. 76), то далее ограничиваемся случаем  .
.
Пусть  - расстояние от точек гиперболы до фокуса
- расстояние от точек гиперболы до фокуса  ,
, 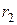 - расстояние до фокуса
- расстояние до фокуса  (рисунок 8).
(рисунок 8).
Определение 18. Числа  и
и 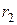 называются фокальными радиусами гиперболы.
называются фокальными радиусами гиперболы.
Пусть  - произвольная точка плоскости. Точка M принадлежит данной гиперболе (данному геометрическому месту точек L) тогда и только тогда, когда
- произвольная точка плоскости. Точка M принадлежит данной гиперболе (данному геометрическому месту точек L) тогда и только тогда, когда
 . (19)
. (19)
Так как
 , (20)
, (20)
 ; (21)
; (21)
то, подставляя (20) и (21) в уравнение (19), получаем, уравнение (22):
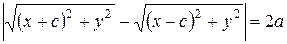 . (22)
. (22)
Для получения канонического уравнения сначала перейдем у уравнению (23):
 . (23)
. (23)
Перенося втрое слагаемое левой части уравнения в правую часть, получаем уравнение (24):
 , (24)
, (24)
возводя в квадрат обе части уравнения (8), и проводя несложные преобразования, получаем уравнение (25):
 ,
,
 ,
,
 ,
,
 ,
,
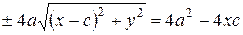 ,
,
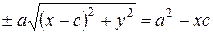 . (25)
. (25)
Снова возводя в квадрат обе части уравнения (25), и проводя необходимые преобразования, получаем уравнением (26):
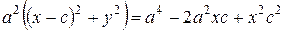 ,
,
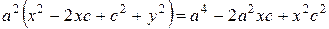 ,
,
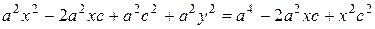 ,
,
 ,
,
 ,
,
 . (26)
. (26)
Как мы уже отметили ранее,  , поэтому
, поэтому  и, следовательно, можно ввести обозначение (27):
и, следовательно, можно ввести обозначение (27):
 , (27)
, (27)
и уравнение (26) можно представить в виде (28):
 . (28)
. (28)
Разделив обе части уравнения (28) на  , получаем уравнение (29):
, получаем уравнение (29):
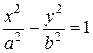 . (29)
. (29)
Так как уравнение (29) является следствием уравнения (22), то координаты любой точки гиперболы будут удовлетворять уравнению (29). Однако в процессе вывода мы использовали метод последовательного возведения в квадрат, следовательно, могли появиться «лишние корни» (И., П., стр. 147; А, стр. 77-78). Поэтому необходимо показать, что любая точка  , координаты которой удовлетворяют уравнению (29) принадлежит рассматриваемой гиперболе, т.е. выполняется равенство (19).
, координаты которой удовлетворяют уравнению (29) принадлежит рассматриваемой гиперболе, т.е. выполняется равенство (19).
|
|
|
Пусть координаты точки  удовлетворяют уравнению (29). Тогда
удовлетворяют уравнению (29). Тогда
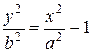 ;
; 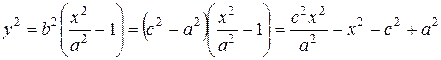 .
.
Опираясь на формулы (20) и (21), получаем, что в этом случае:

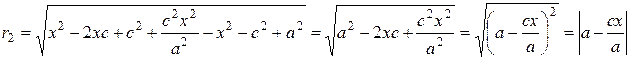 .
.
Из уравнения (29) следует, что 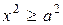 , следовательно,
, следовательно,  .
.
По постановке задачи: 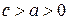 , следовательно,
, следовательно,  . Это означает, что (А, стр. 77) в обоих случаях:
. Это означает, что (А, стр. 77) в обоих случаях:
 (30)
(30)
Следовательно, необходимо рассматривать два случая (в зависимости от того, где лежит точка  ):
):
 , в этом случае точка
, в этом случае точка  лежит в правой полуплоскости;
лежит в правой полуплоскости;
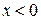 , в этом случае точка
, в этом случае точка  лежит в левой полуплоскости.
лежит в левой полуплоскости.
При  имеем:
имеем:
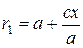 ,
,  , (31)
, (31)
откуда следует, что
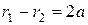 ,
,  ,
,
следовательно, исследуемая точка принадлежит нужному геометрическому месту точек.
При 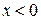 имеем:
имеем:
 ,
, 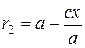 , (32)
, (32)
откуда следует, что
 ,
,  ,
,
следовательно, исследуемая точка также принадлежит нужному геометрическому месту точек.
Определение 19. Уравнение (29) называется каноническим уравнением гиперболы (И.П., стр. 147, А, стр. 79).
Определение 20.. Число 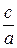 называется эксцентриситетом гиперболы (А, стр. 76).
называется эксцентриситетом гиперболы (А, стр. 76).
В литературе, как и для случая эллипса, встречаются следующие обозначения для эксцентриситета: 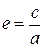 (А, стр. 76) или
(А, стр. 76) или 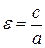 (Г, стр. 52). Выберем второй вариант обозначения:
(Г, стр. 52). Выберем второй вариант обозначения:
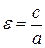 . (33)
. (33)
Как уже было отмечено выше
 . (34)
. (34)
Опираясь на полученные выше результаты, нетрудно получить (А, стр. 78), что
 ; (35)
; (35)
 (36)
(36)
Используя уравнение (29) легко увидеть, что гипербола обладает следующими свойствами (А, стр. 78 – 79, И.П. 149 - 154) (рисунок 9):
1) обе оси гиперболы являются её осями симметрии;
2) центр гиперболы является её центром симметрии;
3) гипербола пересекается только с одной из осей координат, называемой действительной осью, в точках  , которые называются вершинами гиперболы;
, которые называются вершинами гиперболы;
4) не содержит точек в полосе 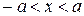 и распадается на две ветви: «правую» (точки которой удовлетворяют условию
и распадается на две ветви: «правую» (точки которой удовлетворяют условию  ) и «левую» (точки которой удовлетворяют условию
) и «левую» (точки которой удовлетворяют условию  ), являющимися симметричными относительно второй оси гиперболы, называемой мнимой осью;
), являющимися симметричными относительно второй оси гиперболы, называемой мнимой осью;
|
|
|
5) при неограниченном удалении от начала координат ветви гиперболы приближаются к прямым 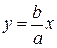 и
и  , которые называются первая и вторая асимптоты соответственно;
, которые называются первая и вторая асимптоты соответственно;
6) асимптоты проходят (содержат в себе) диагонали прямоугольника, ограниченного прямыми 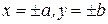 , который, называется основным прямоугольником для данной гиперболы.
, который, называется основным прямоугольником для данной гиперболы.

Рисунок 9 – Г ипербола (http://www.academiaxxi.ru/WWW_Books/HM/Ag/02/05/t.htm)
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 1185; Нарушение авторских прав?; Мы поможем в написании вашей работы!