Правила вывода в исчислении предикатов

Системы аксиом логики предикатов.

Системы аксиом исчисления высказываний остаются верными и в исчислении предикатов первого порядка, только к ним следует добавить еще две аксиомы, которые дают возможность оперировать с кванторами:

1. (" x) P(x)® P(y);

2. P(y) ®$ P(x).

Эти 2 аксиомы, добавленные в классическую систему аксиом или в систему аксиом Новикова, образуют системы аксиом, обладающие свойствами полноты, независимости и непротиворечивости.

Из правил вывода исчисления высказываний в исчислении предикатов действует только правило Modus Ponens. Правило одновременной подстановки модифицировано, а остальные правила вывода касаются выводимости формул, содержащих кванторы.

1. Modus Ponens: Если выводима формула P и выводима формула P ®Q, то выводима и формула Q. Часто это правило записывают следующим образом:
P, P ®Q;
Q

2. Правило одновременной подстановки: если терм t свободен для переменной x в формуле f, то можно подставить терм t вместо переменной x во всех вхождениях x в f.

3. Правило обобщения: если P не содержит свободных вхождений переменной x, то
P®Q(x);
P®"xQ(x)

4. Правило конкретизации: если P не содержит свободных вхождений переменной x, то
Q(x)®P;
$xQ(x)®P

5. Правило переименования. Из выводимости формулы F(x), содержащей свободное вхождение х, ни одно из которых не содержится в области действия кванторов "y и $y следует выводимость F(y).

Пример 6. Докажем правило переименования:

1. +F(x);

2. Из аксиомы 2 классической системы следует, что 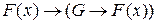, где G – тавтология, не содержащая свободный вхождений x;

3. По правилу Modus Ponens следует, что ;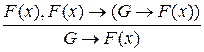

4. Используя правило обобщения, получаем: ;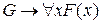

5. По правилу Modus Ponens следует, что ;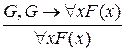

6. Из аксиомы 2 логики предикатов и правила Modus Ponens следует, что .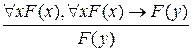

Предваренные (пренексные) нормальные формы исчисления предикатов.

В логике высказываний были введены две нормальные формы – КНФ и ДНФ. В логике предикатов также существуют нормальная форма - ПНФ, которая используется для упрощения процедуры доказательства общезначимости или противоречивости формул.

Определение 22: Формула F логики предикатов находится в предваренной нормальной форме, тогда и только тогда, когда формула F имеет вид:

(K₁x₁)…(K_nx_n) (M), где каждое (K_ix_i), i = 1,…,n, есть или ("x_i) или ($x_i), и M есть формула, не содержащая кванторов. (K₁x₁)…(K_nx_n) называется префиксом, а M – матрицей формулы F.

Законы эквивалентных преобразований логики предикатов.

Законы эквивалентных преобразований логики высказываний используются и в логике предикатов. Кроме них, существуют другие эквивалентные формулы, содержащие кванторы.

Пусть P есть формула, содержащая свободную переменную x. Пусть Q есть формула, которая не содержит переменной x. Тогда следующие пары эквивалентных формул являются законами эквивалентных преобразований логики предикатов:

1. ("x) P(x)Ъ Q=("x) (P(x)Ъ Q);

2. ("x) P(x)Щ Q=("x) (P(x)ЩQ);

3. ($x) P(x)Ъ Q=($x) (P(x)Ъ Q);

4. ($x) P(x)Щ Q=($x) (P(x)ЩQ);

5. Ш(("x) P(x))=($x) (ШP(x));

6. Ш(($x) P(x))=("x) (ШP(x));

7. ("x) P(x)Щ ("x) Q(x)=("x) (P(x)ЩQ(x));

8. ($x) P(x)Ъ ($x) Q(x)=($x) (P(x)Ъ Q(x));

Правила 7 и 8 называются правилами выноса кванторов, которые позволяют распределять квантор всеобщности и квантор существования по операциям конъюнкции и дизъюнкции соответственно. Следует отметить, что нельзя распределять квантор всеобщности и квантор существования по операциям дизъюнкции и конъюнкции соответственно, то есть не эквивалентны следующие пары формул:

("x) P(x) Ъ ("x) Q(x)<>("x) (P(x) ЪQ(x));

($x) P(x) Щ ($x) Q(x)<>($x) (P(x) Щ Q(x));

В подобных случаях можно заменить связанную переменную x в формуле ("x) Q(x) напеременную z, которая не всречается в P(x), так как связанная переменная является лишь местом для подстановки какой угодно переменной. Формула примет вид: ("x) Q(x)= ("z) Q(z). Пусть z не встречается в P(x). Тогда

($x) P(x) Щ ($x) Q(x)= ($x) P(x) Щ ($z) Q(z)

=($x) ($z)(P(x) Щ Q(z)) по правилу 1.

Аналогично, можно написать

("x) P(x) Ъ ("x) Q(x)= ("x) P(x) Ъ ("z) Q(z)

=("x) ("z)(P(x) Ъ Q(z)) по правилу 1.

В общем случае эти правила можно записать в следующем виде:

9.(K₁x) P(x) Ъ (K₂x) Q(x)=(K₁x) (K₂z)(P(x) Ъ Q(z));

10.(K₃x) P(x) Щ (K₄x) Q(x)=(K₃x) (K₄z)(P(x) Щ Q(z)),

где K₁, K₂, K₃, K₄ есть кванторы " или $, а z не входит в P(x).

Когда K₁= K₂=$ и K₃= K₄=", то необязательно переименовывать переменную x, можно прямо использовать правила 7 и 8.

Используя законы эквивалентных преобразований логики высказываний и логики предикатов, всегда можно преобразовать любую формулу в ПНФ.

Алгоритм преобразования формул в ПНФ.

Шаг 1. Используем законы законы 1 и 2 исчисления высказываний для того, чтобы исключить логические связки импликации и эквивалентности.

Шаг 2. Многократно используем закон двойного отрицания, законы де Моргана и законы 5 и 6 исчисления предикатов, чтобы внести знак отрицания внутрь формулы.

Шаг 3. Переименовываем связанные переменные, если это необходимо.

Шаг 4. Используем законы 1, 2, 3, 4, 7,8, 9 и 10 до тех пор, пока все кванторы не будут вынесены в самое начало формулы, чтобы получить ПНФ.

Пример 6. Приведем формулу ("x) P(x) ® ($x) Q(x) к ПНФ:

("x) P(x) ® ($x) Q(x)=Ш(("x) P(x))Ъ ($x) Q(x)(по закону 1 логики высказываний)

=($ x)(Ш P(x)) Ъ ($ x)) Q(x)(по закону 5 логики предикатов)

=($ x)(Ш P(x) Ъ Q(x))(по закону 8 логики предикатов), что и есть ПНФ исходной формулы.

Дата добавления: 2015-06-27