Основной закон динамики для частицы идеальной жидкости

Каждая частица текущей жидкости (газа) испытывает воздействие со стороны окружающих частиц, это воздействие определяется давлением р. Мы уже виде­ли, что изменение давления определяет ускорение движущейся частицы. Исходя из этих представлений, выведем основной закон динамики для частицы жидкости. Предположим, что выделена частица в форме куба объемом dx=dx ₁ dx ₂ dx ₃, находящаяся в точке r (х ₁, х ₂, х ₃)(рис. 285). На каждую грань кубика действует сила давления. Например, на грань dx ₁ dx ₂снизу действует усилие рdx ₁ dx ₂, а на противополож­ную грань — усилие

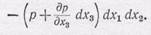
¹) Распределение давления определено по закону Бернулли, который выво­дится в следующих параграфах.

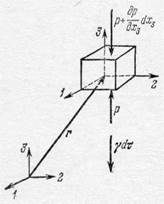
Рис. 285.

Поэтому вдоль оси 3 на кубик действует сила

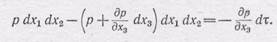
Кроме этого, на частицу действует сила тяготения, равная

направленная противоположно оси 3 (здесь g— удельный вес жид­кости). Тогда по второму закону динамики:

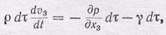
или

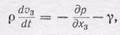(101.1)

где v ₃ — компонента скорости по оси 3.

Вследствие достаточной малости объема d tмы считаем, что плотность r постоянна по всему объему. Также давление р на гра­нях кубика одинаково во всех точках и одинаковы скорости v.

Аналогичным путем найдем, что в направлении двух других осей

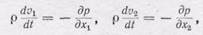(101.2)

так как сила тяжести направлена вдоль оси 3.

Теперь можно записать три формулы (101.1) и (101.2) в вектор­ном виде. Если е ₁, е ₂, e ₃— единичные векторы по осям координат, то

или

(101.3)

где вектор обозначен символом grad р и называется градиентом ¹) давления р, вектор— g e ₃ = r g, где g — век­тор ускорения тяготения.

Формула (101.3) выражает основной закон гидродинамики для идеальной (без трения) жидкости или газа. В нестационарном по­токе все величины r, v, p зависят от места r и времени t. В стацио­нарном — только от места r, поэтому при рассмотрении стационар­ного течения удобно воспользоваться представлением о трубках

¹) Градиент иногда обозначают с помощью символического вектора 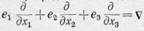, тогда

тока: они постоянны, и закон динамики для идеальной жидкости в достаточно тонкой трубке тока можно описать следующим образом. Скорость v = v (s) является функцией только координаты s (коорди­наты вдоль осевой линии трубки). Частица, которая в момент вре­мени t имела координату s, за время dt сдвинется на отрезок ds ₁(рис. 286). Скорость частицы в новом положении будет другая, какая-то v ₁, которую всегда можно представить так:

Следовательно, разность скоростей ча­стицы в момент времени t и момент времени t + dt дает приращение ско­рости частицы

Заменив в этом выражении смещение частицы ds ₁на v (s) dt, полу­чаем

(101.4)

Ускорение частицы при стационарном течении равно производной вдоль оси трубки тока от половины квадрата скорости потока. Поэтому основное уравнение динамики для частицы идеальной жидкости (101.3) в этом случае можно записать так:

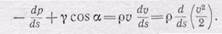(101.5)

Здесь a— угол между вертикалью и направлением осевой линии трубки тока в данном сечении. Это уравнение справедливо для стационарного течения как несжимаемой жидкости, лишенной вязкости, так и для сжимаемого газа, не обладающего внутрен­ним трением.

Остановимся на определении ускорения частицы dv/dt в общем случае нестацио­нарного течения, когда нам известно поле v (r, t). Мы видели, что ускорение частицы вдоль трубки тока в стационарном течении равной vdv/ds, т. е. определяется изменением скорости вдоль трубки. Но этот же результат можно получить, не прибегая к рассмотрению трубок тока.

В момент t скорость частицы, движущейся через точку r, равна v (r, t), а через отрезок времени dt частица будет находиться в точке r + d r и скорость будет равна v ( r + d r, t + dt). Тогда приращение скорости этой частицы

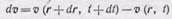(101.6)

Рис. 286.

иускорение = dv/dt. Разобьем приращение d v на две части: в первой определяется (d v)_t — приращение только вследствие изменения времени, во второй {d v)_r — приращение v вследствие изменения места частицы (на рис. 287 вычерчена еще скорость v ( r + d r, t) — скорость, которую имела другая частица, находив­шаяся в точке r + d r в момент t). Поэтому

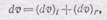(101.7)

где

(101.8)

В стационарном потоке ускорение определяется только (dv)_r, так как (dv)_t = 0, ибо скорость в каждой точке пространства не зависит от времени. В нестационарном потоке, вообще говоря, оба члена отличны от нуля. Первый член

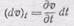
определяется частной производной от v при r = const. Второй член (дифференциал (d v) _r) имеет более сложный вид, он зависит от «производной по направлению», по d r, при t =const, эту производную иногда записывают d v /d r. Вычислять (d v)_r нужно как при­ращение вектора v при изменении места на d r в стационарном потоке. Такое прираще­ние в постоянном векторном поле при пере­мещении на d r мы уже рассматривали, анализируя малые деформации упру­гого тела (§ 86). Каждая компонента скорости: v₁, v₂, v ₃— является функцией трех переменных: х ₁, x ₂, х ₃.Напомним, что v=v ₁ e ₁+ v ₂ e ₂+ v ₃ e ₃и r = x ₁ e ₁+ х ₂ е ₂+ x ₃ e ₃, где е ₁, е ₂, е ₃— орты прямоугольной системы коор­динат. Тогда приращения компонент скорости можно записать так:

(101.9)

и Рассматривая систему (101.9), мы видим, что

ее можно представить в виде произведения тензора U на вектор d r = dx ₁ e ₁+ dx ₂ e ₂+ dx ₃ e ₃в таком виде:

(101.10)

где

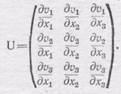(101.11)

Так как в данном случае идет речь о приращении скорости определенной частицы, которая за время dt сдвинулась из точки r на d r, to dr = v dt. Подставляя это

Рис. 287.

в (101.10), получаем

(101.12)

или ускорение частицы dv/dt, учитывая (101.7) и (101.12), теперь можно записать так:

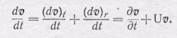(101.13)

Это и есть общее выражение для ускорения частицы. Первая часть — частная производная по t, вторая — произведение тензора (101.11) на v. В стационарном потоке dv/dt= 0 и

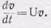(101.14)

Если скорость, плотность и давление потока зависят только от одной координаты и скорость направлена по этой координате, например, если v ₁¹0, v ₂= v₃ =0

и все производные по х ₂и х ₃ равны нулю, то dv ₁/ dt=v ₁ дv ₁ /дx ₁, как мы видели раньше

в (101.4), где x ₁ =s и v ₁ =v. Давление р — также функция только х ₁,и поэтому уравнение гидродинамики (101.3), если пренебречь тяготением, в этом случае принимает вид

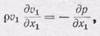
как получено ранее (см. (101.5)).

Дата добавления: 2015-06-28