Интегральные характеристики сечений

В расчётные формулы для определения напряжений входят характеристики сечений тел, назы­ваемые интегральными (геометрическими) характеристиками плоских сечений (плоских фигур). При растяжении (сжатии), кручении, изгибе и более сложных видах нагружения используют следующие интегральные характеристики се­чений тел: площадь сечения, статические моменты, моменты инерции, моменты сопротивления, радиусы инерции. Во многих литературных источниках ис­пользуют расчетные формулы напряжений, в которые входят интегральные характеристики сечений относительно главных центральных осей. Для опреде­ления положения таких осей, в частности, требуется найти поло­жение центра тяжести сечения. Поэтому при изучении интегральных характеристик сечений определённое внимание от­водится выработке умения определять положение центра тяжести и положение главных центральных осей. Объясняется это тем, что выражения интегральных характеристик сечений относительно главных центральных осей оказываются проще, чем относительно других координатных осей, что позво­ляет получать относительно простые расчётные формулы для вычисления на­пряжений и деформаций.

Определение интегральных характеристик сечений сводится к вычис­лению определённых интегралов. Поэтому при непрерывной подготовке по фундаментальным дисциплинам представляются необходимыми навыки, полученные студентами при изучении курса высшей математики, в частности, при изуче­нии интегрального и дифференциального исчислений.

Одним из основных объектов при инженерных расчётах является стержень – тело, у которого один параметр (длина) намного больше двух других (высоты и ширины). При действии на стержень внешних нагрузок в его сечениях в общем случае возникают шесть интегральных характеристик напряжений (ИХН):

(1.1)

где Q _x, Q _y – поперечные силы; Q _z =N – продольная сила; M _x, M _y – изгибающие моменты; M _z = M _k – крутящий момент; 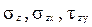– нормальное и касательные напряжения.

Зная величину и место приложения внешних нагрузок, можно определить ИХН. По известным ИХН можно определить величину напряжений и относительных деформаций и затем производить проверочные или проектные расчёты на прочность, жесткость, устойчивость и др.

Для изотропного материала, подчиняющегося закону Гука, нормальные напряжения s_z, при одноосном напряжённом состоянии вычисляют по формуле

(1.2)

где e₀ – относительное удлинение начального волокна; K _x, K_y – кривизны проекций изогнутого начального волокна на плоскости, перпендикулярные соответственно осям OXи OY; x, y – координаты точки сечения, где определяют s _z; Е– модуль нормальной упругости.

Используя уравнения (1.1) и (1.2), можно, в частности, получить ИХН для стержней постоянного поперечного сечения:

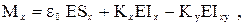
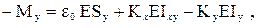(1.3)

где введены следующие обозначения:

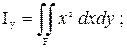
(1.4)

Эти величины называют интегральными характеристиками сечений (ИХС), они могут быть вычислены для любого плоского сечения (плоской фигуры) относительно координатных осей, произвольно выбранных в плоскости сечения.

1.1. Площадь и статические моменты сечений

Интегральная характеристика сечения, зависящая только от формы и размеров сечения, является площадью сечения и определяется как

(1.5)

Интегральные характеристики сечения, зависящие как от формы и размеров сечения, так и от его расположения относительно координатных осей, называют статическими моментами и определяют по формулам

(1.6)

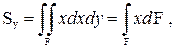(1.7)

Размерность статического момента - единица длины в кубе. В зависимости от выбора осей координат статические моменты могут принимать положительные и отрицательные значения, быть равными нулю.

1.2. Осевые и центробежный моменты инерции

Интегральные характеристики сечений, вычисляемые по формулам

(1.8)

(1.9)

называют осевыми моментами инерции сечения относительно осей OX и OY. Размерность осевого момента инерции сечения – единица длины в четвертой степени. Осевые моменты инерции всегда положительны и не равны нулю. Интегральная характеристика сечения, вычисляемая по формуле

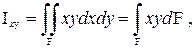
(1.10)

называется центробежным моментом инерции сечения относительно двух взаимно перпендикулярных осей OX иOY. Размерность центробежного момента инерции - единица длины в четвертой степени. Центробежный момент может быть, как и статические моменты S _x, и S_y, положительным, отрицательным или равным нулю.

1.3 Определение интегральных характеристик сечений

при параллельном переносе осей

Предположим, что в системе координатных осей OX иOY известны такие ИХС плоской фигуры (рис. 1.1), как S _x, S_y, I _x, I_y, I _{x y}. Требуется определить одноименные ИХС относительно осей O₁X₁ иO₁Y₁, параллельных осямOX иOY. Известно также, что расстояние между осями OX и O₁X₁равно " а ", а между осями OY и O₁Y₁ –"b".

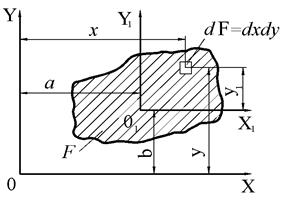
Рис. 1.1

(1.11)

(1.12)

Осевые и центробежные моменты сечения относительно осей O₁X₁ и O₁Y₁:

(1.13)

(1.14)

(1.15)

1.4. Определение координат центра тяжести сечения

и положения центральных осей

Из формул (1.11), (1.12) следует, что при соответствующем выборе координатных осей O₁X₁ иO₁Y₁статические моменты относительно них могут стать равными нулю. Оси, относительно которых статические моменты равны нулю, называют центральными осями, а точку пересечения таких осей – центром тяжести.

Координаты центра тяжести сечения относительно произвольно выбранных осей OX иOYопределяют по формулам

(1.16)

Если сечение имеет ось симметрии, то эта ось всегда совпадает с одной из

центральных осей. Полагая, что оси OX и OY центральные, из (1.13) – (1.15) получим

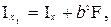
(1.17)

Из первых двух формул (1.17) следует, что в семействе параллельных осей минимальный момент инерции получается относительно центральной оси (a = 0 или b= 0). Поэтому при переходе от центральных осей к нецентральным осевые моменты инерции увеличиваются, и величины a² Fи b² F следует к моментам инерции прибавлять, а при переходе от нецентральных осей к центральным – вычитать.

При вычитании центрального момента инерции по формулам (1.17) следует учитывать знак величин a и b.

1.5. Определение осевых и центробежного моментов инерции

при повороте координатных осей

При повороте координатных осей OX иOYна угол a (рис. 1.2) координаты x ₁ и y₁ элементарной площади d F относительно осей OX₁ и OY₁ определяются как

Рис.1.2

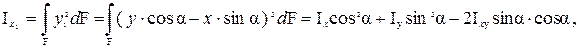(1.18)

(1.19)

(1.20)

Из формул (1.18) – (1.20) следует, что при повороте осей OX и OY на 90°

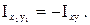
Поскольку величина центробежного момента изменилась при повороте осей OX иOY на 90° от до минус , то, очевидно, что при некотором значении угла 0<a<90° центробежный момент инерции сечения будет равен нулю, а осевые моменты инерции примут максимальное и минимальное значения. Оси координат, относительно которых центробежный момент равен нулю, называют главными осями. Осевые моменты инерции, определённые относительно таких осей, называют главными моментами инерции. Если главные оси совпадают с центральными, то их называют главными центральными осями инерции. Осевые моменты сечения, определённые относительно главных центральных осей, называют центральными моментами инерции.

[В.В.,В.Н1]!!!!!1.6. Определение положения главных центральных осей и

главных моментов инерции сечения

Величину главных моментов инерции и положение главных осей можно определить из соотношений [4]

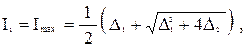
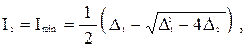(1.21)

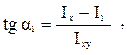(1.22)

(1.23)

где D₁ = I _x +I_y – первый инвариант моментов инерции; – второй инвариант моментов инерции; a₁, a₂– углы поворота главных осей OX₁ и OY₁относительно центральной оси OX.

Если центральные оси сечения обозначить OX_c Y_c , а главные оси - OX₀ Y₀, то из (1.18), (1.19), (1.23) после несложных преобразований получим

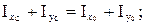
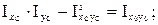
(1.24)

Выражение (1.24) используют, как правило, для проверки правильности решения задач.

1.7. Полярный момент инерции сечения

Рис. 1.3

Между полярным моментом инерции I_p и осевыми моментами инерции существует связь

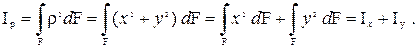(1.26)

1.8. Моменты сопротивления сечения

Осевым моментом сопротивления сечения называют отношение момента инерции относительно координатной оси к расстоянию от этой оси до наиболее уда­ленной точки поперечного сечения

(1.27)

Полярным моментом сопротивления называют отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения

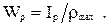(1.28)

Размерность моментов сопротивления сечений - единица длины в кубе.

1.9. Радиусы инерции сечения

Осевыми радиусами инерции сечения относительно осей OX и OY называют соотношения

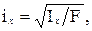
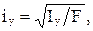(1.29)

где F – площадь поперечного сечения; I _x, I_y – моменты инерции относительно осей OX и OY.

Полярным радиусом инерции сечения относительно полюса называют выражение

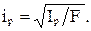(1.30)

Размерность радиуса инерции – единица длины.

1.10. Интегральные характеристики сложных плоских фигур

Сложными будем считать плоские сечения, ИХС которых не могут быть вычислены, как для односвязного контура. Для фигуры (рис.1.4) любую ИХС можно получить алгебраическим суммированием ИХС простых фигур, составляющих исходную:

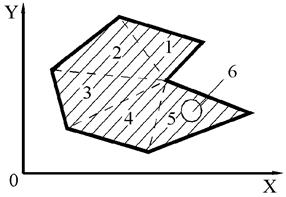
Рис. 1.4

1.11. Определение интегральных характеристик сечений стержней

с криволинейной осью

Известно [4], что нормальные напряжения в поперечном сечении стержня с криволинейной осью определяются по формуле

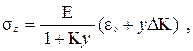(1.32)

где E – модуль нормальной упругости; K=1/r – кривизна оси недеформированного стержня; r - радиус кривизны оси недеформированного стержня; y - расстояние от главной центральной оси сечения стержня до волокна, где вычисляются напряжения.

Из системы уравнений

определяют параметры а и с.

В системе (1.33) коэффициенты A, B, C являются ИХС заданной плоской фигуры, которые определяют как

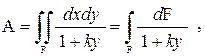
(1.34)

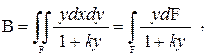(1.35)

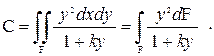(1.36)

Если в качестве осей координат выбрать главные центральные оси плоской фигуры, то между величинами A, B, C устанавливается простая зависимость:

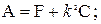
(1.37)

Из уравнений (1.37) следует, что достаточно вычислить одну из величин В, А или С, как оставшиеся определяются однозначно. Эксцентриситет (ордината упругого

центра) плоской фигуры криволинейного стержня определяют по формуле

(1.38)

Из формул (1.34) – (1.36) видно, что если кривизна стержня k =0, то A=F, B=S _x, C=I _x.

Алгоритм определения центра тяжести сечения

и его главных моментов инерции

1. Разделить заданную фигуру на простые фигуры (т.е. такие фигуры, моменты инерции которых могут быть найдены по определению или даны в справочниках).

2. Выписать геометрические характеристики каждой из простых фигур (координаты центра тяжести, площадь, осевые и центробежный моменты инерции, угол, определяющий положение главных осей инерции данной фигуры).

3. Выбрать оси X, Y для определения координат центра тяжести всей фигуры (оси относительно которых можно просто определить координаты центра тяжести составляющих фигур).

4. Определить координаты x _i, y _i центров тяжести составляющих фигур относительно осей X, Y.

5. Определить статические моменты площади всей фигуры относительно осей X, Y: Необходимо обратить внимание на знак координат x _ci, y _ci.

6. Определить координаты x ₀ , y ₀ центра тяжести всей фигуры относительно осей X, Y. _. Для контроля можно использовать правило: общий центр тяжести двух фигур лежит на отрезке, соединяющем их центры тяжести, и делит его на части, обратно пропорциональные площадям фигур.

7. Выбрать центральные оси всей фигуры. Эти оси целесообразно выбрать так, чтобы они были параллельны главным центральным осям инерции большинства составляющих фигур. Если фигура имеет ось симметрии, то одна из осей (X_сi или Y_сi) направляется по этой оси.

8. Определить осевые моменты инерции каждой из составляющих фигур относительно ее центральных осей, параллельных осям X₀, Y₀. В некоторых случаях удобнее сначала определить геометрические характеристики относительно осей X, Y, а затем выполнить параллельный перенос осей и найти моменты инерции относительно центральных осей X₀, Y₀. (Если главные центральные оси инерции данной фигуры не параллельны осям X₀, Y₀, нужно использовать формулы для моментов инерции относительно повёрнутых осей.)

9. Определить координаты центров тяжести составляющих фигур относительно центральных осей X₀, Y₀.

10. Определить осевые моменты инерции всей фигуры относительно осей X₀, Y₀. (Осевой момент инерции сложной фигуры относительно какой-нибудь оси равен сумме осевых моментов инерции составляющих фигур относительно той же самой оси. Осевой момент инерции фигуры относительно оси, параллельной её центральной оси, равен осевому моменту инерции данной фигуры относительно центральной оси, увеличенному на произведение площади фигуры на квадрат расстояния между осями.)

11. Определить центробежные моменты инерции каждой из составляющих фигур относительно ее центральных осей, параллельных осям X₀, Y₀. (Если известен центробежный момент инерции данной фигуры относительно других осей, не параллельных осям X_С, Y_С, необходимо использовать формулу центробежного момента инерции относительно повернутых осей.) При пользовании справочными данными необходимо обратить внимание на выбор положительного направления осей координат; при повороте координатных осей на угол 90° знак центробежного момента инерции изменяется.

12. Определить центробежный момент всей фигуры относительно осей X₀, Y₀. (Центробежный момент инерции сложной фигуры относительно какой-нибудь пары взаимно перпендикулярных осей равен сумме центробежных моментов инерции составляющих фигур относительно тех же осей. Центробежный момент инерции фигуры относительно осей, параллельных ее центральным осям, равен

центробежному моменту инерции относительно центральных oсей, увеличенному на произведение площади фигуры на координаты ее центра тяжести относительно новых осей.)

13. Определить положение главных центральных осей по формулам (1.22), (1.23).

14. Определить моменты инерции всего сечения относительно главных центральных осей инерции по формуле (1.21). Для контроля вычислений следует воспользоваться соотношениями (1.24).

Для приобретения устойчивых навыков по определению ИХС в прил. 1 приведены варианты индивидуальных заданий.

Дата добавления: 2015-06-28