Решение уравнений Лапласа и Пуассона

В результате на выходе получаем решение в табличном виде

x y	x1	x2	…	xn
y1	U1,1	U1,2	…	U1,n
y2	U2,1	U2,2	…	U2,n
y3	U3,1	U3,2	…	U3,n

Неявная схема решения

Перепишем уравнение (***) в виде

.

Т. о. решение на j-ом слое представляется через решение на j-1 слое. Её решение на j-ом слое осуществляется так же как решение ОДУ 2 порядка, т.е. сводятся к решению системы линейных уравнений с 3-х диагональной матрицей.

Поэтому р.с. называют неявной.

Явная расчётная схема является устойчивой при условии , а неявная р.с. при любом соотношении шагов h и t. Поэтому неявная р.с называется условно устойчивой, а неявная абсолютно устойчивой.

Для решения уравнений Пуассона и Лапласа (частный случай, когда ) – уравнений эллиптического типа – предназначена функция relax(a, b, c, d, e, f, u, rjac), реализующая метод релаксации. Фактически, эту функцию можно использовать для решения эллиптического уравнения общего вида

которое может быть сведено к уравнению в конечных разностях

В частности, для уравнения Пуассона коэффициенты .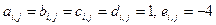

Идея метода релаксации заключается в следующем. Если нет источников (уравнение Лапласа), то значение функции в данном узле на текущем шаге 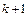определяется как среднее значение функции в ближайших узлах на предыдущем шаге k

При наличии источников разностная схема имеет вид

Метод релаксации сходится достаточно медленно, так как фактически он использует разностную схему с максимально возможным для двумерного случая шагом .

В методе релаксации необходимо задать начальное приближение, то есть значения функции во всех узлах области, а так же граничные условия.

Функция relax возвращает квадратную матрицу, в которой:

1) расположение элемента в матрице соответствует его положению внутри квадратной области,

2) это значение приближает решение в этой точке.

Эта функция использует метод релаксации для приближения к решению.

Вы должны использовать функцию relax, если Вы знаете значения искомой функции u(x, y) на всех четырех сторонах квадратной области.

Аргументы:

a, b, c, d, e – квадратные матрицы одного и того же размера, содержащие коэффициенты дифференциального уравнения.

f – квадратная матрица, содержащая значения правой части уравнения в каждой точке внутри квадрата

u – квадратная матрица, содержащая граничные значения функции на краях области, а также начальное приближение решения во внутренних точках области.

rjac – Параметр, управляющий сходимостью процесса релаксации. Он может быть в диапазоне от 0 до 1, но оптимальное значение зависит от деталей задачи.

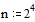
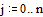
Задаем правую часть уравнения Пуассона – два точечных источника

Задаем значения параметров функции relax

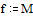
Задаем граничные условия и начальное приближение – нули во всех внутренних точках области

Находим решение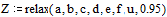

и представляем его графически в виде поверхности и линий уровней.

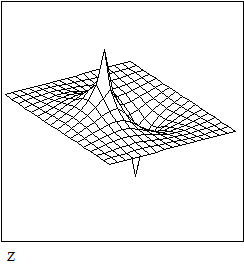
Если граничные условия равны нулю на всех четырех сторонах квадрата, можно использовать функцию multigrid.

Алгоритм метода достаточно громоздкий, поэтому рассматривать его мы не будем.

Дата добавления: 2015-06-27