
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнения первого порядка 1 страница
|
|
|
|
КУРС
.
14.3. Применения двойного интеграла:
· 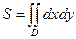 или
или 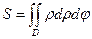 - вычисление площади фигур;
- вычисление площади фигур;
·  - вычисление объема;
- вычисление объема;
· 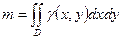 - масса плоской неоднородной пластины плотности
- масса плоской неоднородной пластины плотности 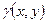 (механический смысл двойного интеграла);
(механический смысл двойного интеграла);
· 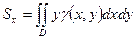 ;
; 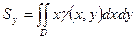 - статические моменты относительно осей;
- статические моменты относительно осей;
· 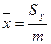 ;
; 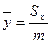 - координаты центра масс пластины;
- координаты центра масс пластины;
· Моменты инерции пластины:
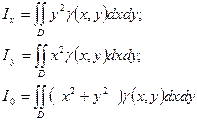
14.4. Определение и вычисление тройного интеграла:
Пусть функция 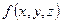 непрерывна в замкнутой области
непрерывна в замкнутой области 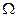 .
.
 Определение: конечный предел интегральной суммы функции
Определение: конечный предел интегральной суммы функции 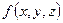 в области
в области 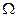 при условии, что
при условии, что  и
и 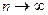 называется тройным интегралом от этой функции по области
называется тройным интегралом от этой функции по области 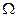 , где
, где 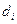 - диаметр частичной области.
- диаметр частичной области.
Т.о. 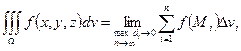 , где
, где 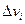 - объем каждой частичной области.
- объем каждой частичной области.
Вычисление тройных интегралов:
1. В декартовой системе координат:
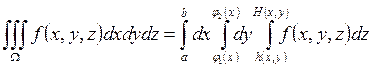
2. В цилиндрической системе координат (ц.с.к.):
 Определение: цилиндрическими координатами т.
Определение: цилиндрическими координатами т. 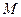 называется тройка чисел
называется тройка чисел 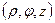 , где
, где 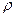 и
и 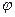 - полярные координаты проекции т.
- полярные координаты проекции т. 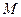 на плоскость
на плоскость 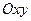 ,
,  - аппликата т.
- аппликата т. 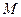 .
.
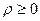 ,
, 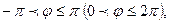
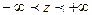 .
.
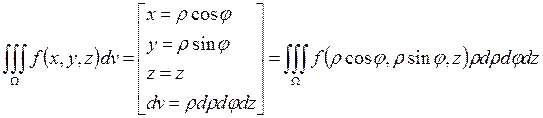
При переходе к цилиндрическим координатам полезно использовать: 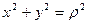 .
.
Тройной интеграл целесообразно вычислять в ц.с.к., если:
- область интегрирования 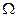 ограничена хотя бы одной из поверхностей
ограничена хотя бы одной из поверхностей 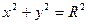 (прямой круговой цилиндр),
(прямой круговой цилиндр), 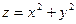 (параболоид вращения),
(параболоид вращения), 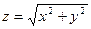 (прямой круговой конус) с
(прямой круговой конус) с 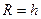 ;
;
- область 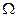 проецируется на плоскость
проецируется на плоскость 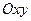 в круг или любую его часть.
в круг или любую его часть.
3. В сферической системе координат (с.с.к.):
 Определение: тройка чисел
Определение: тройка чисел 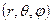 называется сферическими координатами т.
называется сферическими координатами т. 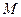 , где
, где 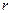 - длина радиус-вектора точки,
- длина радиус-вектора точки, 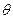 - величина угла между осью
- величина угла между осью 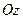 и радиус - вектором,
и радиус - вектором, 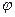 - полярный угол проекции т.
- полярный угол проекции т. 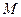 на плоскость
на плоскость 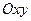 .
.
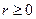
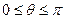
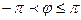
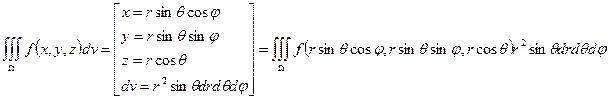
Тройной интеграл целесообразно вычислять в с.с.к., если 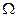 - шар или его часть.
- шар или его часть.
При переходе к сферическим координатам полезно использовать, что 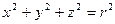 .
.
|
|
|
14.5. Применения тройного интеграла:
· 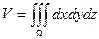 - объем тела в декартовой системе координат;
- объем тела в декартовой системе координат;
· 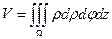 - объем тела в цилиндрической системе координат;
- объем тела в цилиндрической системе координат;
· 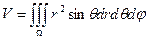 - объем тела в сферической системе координат;
- объем тела в сферической системе координат;
· 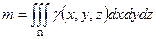 - масса неоднородного тела
- масса неоднородного тела 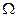 с плотностью
с плотностью 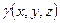 ;
;
· Статические моменты относительно координатных плоскостей:
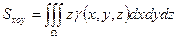 ;
;
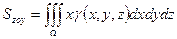 ;
;
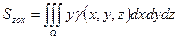 .
.
· 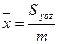 ;
; 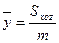 ;
; 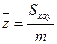 - координаты центра масс;
- координаты центра масс;
· Моменты инерции тела относительно координатных осей:
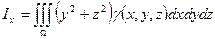 ;
;
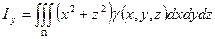 ;
;
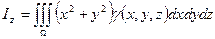 ;
; 
· Моменты инерции тела относительно координатных плоскостей:
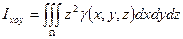 ;
;
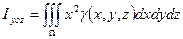 ;
;
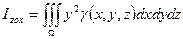
Момент инерции относительно 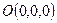 :
:
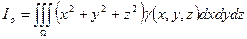 .
.
РАЗДЕЛ XV. КРИВОЛИНЕНЙНЫЕ ИНТЕГРАЛЫ
15.1. Криволинейный интеграл по длине дуги (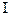 рода):
рода):
Пусть 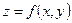 непрерывна в каждой точке гладкой дуги
непрерывна в каждой точке гладкой дуги 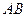 .
.
 Определение: конечный предел интегральной суммы функции
Определение: конечный предел интегральной суммы функции 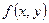 на кривой
на кривой 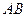 при условии, что
при условии, что 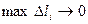 и
и 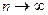 называется криволинейным интегралом по длине дуги от функции
называется криволинейным интегралом по длине дуги от функции 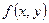 по кривой
по кривой 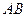 , где
, где 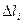 - длина полученных частичных дуг
- длина полученных частичных дуг 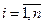 .
.
Т.о. 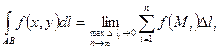 .
.
Основные свойства:
1) 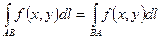 ;
;
2) 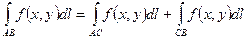 ;
;
3) Если в каждой точке дуги 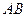
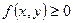 , то и
, то и 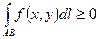 ;
;
4) Если в каждой точке дуги 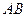
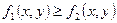 , то и
, то и
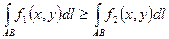 ;
;
5) 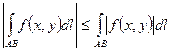 ;
;
6) 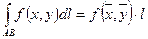 , где
, где  - длина дуги
- длина дуги 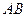 ,
,  - точка дуги.
- точка дуги.
15.2. Вычисление криволинейных интегралов по длине дуги:
· 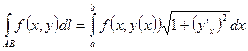 - в случае явного задания кривой интегрирования
- в случае явного задания кривой интегрирования 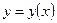 ;
;
· 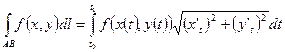 - в случае параметрического задания кривой интегрирования
- в случае параметрического задания кривой интегрирования 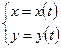 ;
;
· 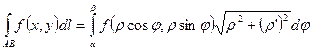 - в случае задания кривой интегрирования в п.с.к.
- в случае задания кривой интегрирования в п.с.к. 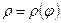 .
.
15.3. Применения криволинейного интеграла по длине дуги:
· 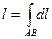 - длина дуги;
- длина дуги;
· 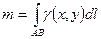 - масса неоднородной дуги с плотностью
- масса неоднородной дуги с плотностью 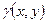 ;
;
· 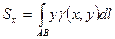 ;
; 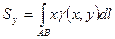 - стат. моменты дуги относительно координатных осей;
- стат. моменты дуги относительно координатных осей;
· 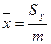 ;
; 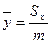 - координаты центра масс дуги;
- координаты центра масс дуги;
· Моменты инерции дуги:
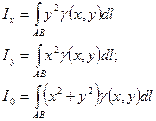
15.4. Криволинейный интеграл по координатам (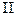 рода):
рода):
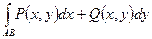 - составной криволинейный интеграл.
- составной криволинейный интеграл.
 Пусть
Пусть 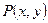 - непрерывна в каждой точке гладкой направленной дуги
- непрерывна в каждой точке гладкой направленной дуги 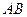 .
.

Определение: конечный предел интегральной суммы функции 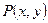 на кривой
на кривой 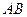 при условии, что
при условии, что 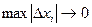 и
и  называется криволинейным интегралом по координате
называется криволинейным интегралом по координате 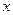 от функции
от функции 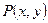 по кривой
по кривой 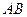 , где
, где 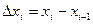
Т.о. 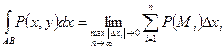 , где
, где 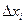 - величины полученных частичных проекций на ось
- величины полученных частичных проекций на ось 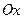 частичных дуг.
частичных дуг.
|
|
|
Аналогично 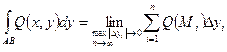 .
.
Основные свойства:
1) 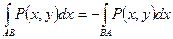 ;
;
2) 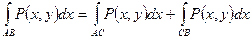 ;
;
3) Криволинейные интегралы по координатам, взятые по замкнутому контуру 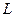 не зависят от выбора на контуре начальной точки, но зависят от направления обхода контура.
не зависят от выбора на контуре начальной точки, но зависят от направления обхода контура.
Если направление обхода не указано, то полагают, что контур обходится в положительном направлении (такое, при котором точки области, ограниченные контуром, остаются слева).
15.5. Вычисление криволинейных интегралов по координатам:
1. 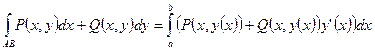 - в случае явного задания кривой интегрирования
- в случае явного задания кривой интегрирования 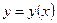 ;
;
2. 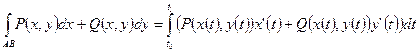 - в случае
- в случае
параметрического задания кривой интегрирования 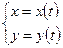 ;
;
3.  - формула Грина, где
- формула Грина, где 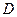 - область, ограниченная контуром
- область, ограниченная контуром 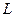 .
.
4. Если  , то
, то 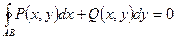 ;
;
5. Если  и
и 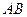 - незамкнутая кривая, то
- незамкнутая кривая, то
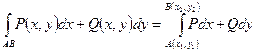 , т.е. вычисление таких интегралов сводится к вычислению определенных, однако, в качестве линии интегрирования удобно брать ломаную, звенья которой параллельны осям координат.
, т.е. вычисление таких интегралов сводится к вычислению определенных, однако, в качестве линии интегрирования удобно брать ломаную, звенья которой параллельны осям координат.
15.6. Применения криволинейных интегралов по координатам:
1.  - нахождение функции по ее полному дифференциалу, где
- нахождение функции по ее полному дифференциалу, где 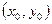 - точка из области непрерывности
- точка из области непрерывности 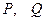 ;
;
2. 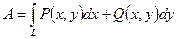 - работа силы
- работа силы 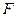 , где
, где 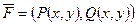 , по перемещению материальной точки
, по перемещению материальной точки  ;
;
3. 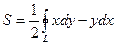 - площадь плоской фигуры.
- площадь плоской фигуры.
Теорема (условие независимости составного интеграла по координатам от формы кривой интегрирования):
Если функции  и их частные производные первого порядка непрерывны в некоторой области
и их частные производные первого порядка непрерывны в некоторой области 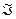 , то для того чтобы составной интеграл по координатам не зависел от формы кривой интегрирования необходимо и достаточно, чтобы в каждой точке области
, то для того чтобы составной интеграл по координатам не зависел от формы кривой интегрирования необходимо и достаточно, чтобы в каждой точке области 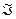 подынтегральное выражение
подынтегральное выражение 
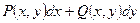 было полным дифференциалом некоторой функции двух переменных
было полным дифференциалом некоторой функции двух переменных 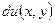 .
.
РАЗДЕЛ XVI. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
16.1. Поверхностный интеграл по площади поверхности 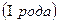 :
:
 Пусть функция
Пусть функция 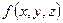 - непрерывна в каждой точке гладкой поверхности
- непрерывна в каждой точке гладкой поверхности  .
.
Определение: конечный предел интегральной суммы функции 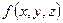 в области
в области  при условии, что
при условии, что 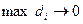 и
и  называется поверхностным интегралом по площади поверхности от функции
называется поверхностным интегралом по площади поверхности от функции 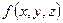 по поверхности
по поверхности  , где
, где 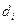 - диаметр частичной поверхности.
- диаметр частичной поверхности.
Т.о. 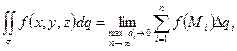 , где
, где 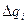 - площадь частичной
- площадь частичной
поверхности.
Определение: сторона поверхности называется положительной (отрицательной) в направлении оси  , если нормаль, проведенная к этой стороне в произвольной точке составляет с осью
, если нормаль, проведенная к этой стороне в произвольной точке составляет с осью  острый (тупой) угол.
острый (тупой) угол.
Аналогично, для осей 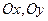 .
.
|
|
|
Определение: выбор одной из двух сторон поверхностей (положительной или отрицательной) в направлении определенной оси называется ориентацией поверхности в направлении выбранной оси.
Основные свойства:
1. Поверхностные интегралы не завися от ориентации поверхности в направлении любой оси.
2. 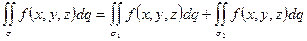 ;
;
3. Если всюду на 
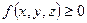 , то и
, то и 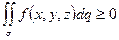 ;
;
4. Если всюду на 
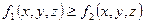 , то и
, то и 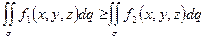 ;
;
5. 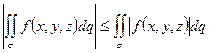 ;
;
6. 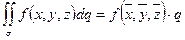 , где
, где 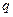 - площадь
- площадь  ,
, 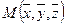 - из поверхности
- из поверхности  .
.
16.2. Вычисление поверхностных интегралов по площади поверхности:
1. Выясняем, прямая параллельная какой оси, пересекает эту поверхность не более чем в одной точке;
2. Тогда уравнение  разрешаем относительно этой переменной, проецируем
разрешаем относительно этой переменной, проецируем  на соответствующую двумерную плоскость.
на соответствующую двумерную плоскость.
Например, если такая прямая параллельна оси  , то
, то
- уравнение  :
:  ;
;
- проецируем  на
на 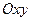 и находим по формуле
и находим по формуле 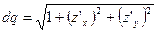 .
.
3. Переходим к двойному интегралу:
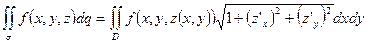 .
.
16.3. Применения поверхностных интегралов по площади поверхности:
· 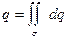 - площадь поверхности
- площадь поверхности  ;
;
· 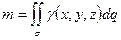 - масса гладкой неоднородной поверхности
- масса гладкой неоднородной поверхности  с плотностью
с плотностью 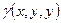 ;
;
· Статические моменты относительно координатных плоскостей:
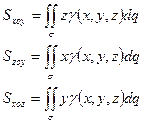 -;
-;
· 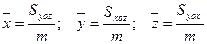 - координаты центра масс поверхности;
- координаты центра масс поверхности;
· Моменты инерции поверхности относительно координатных осей:
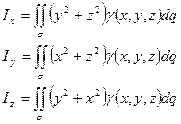
16.4 Поверхностный интеграла по координатам 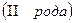 :
:

Пусть имеет гладкую поверхность  , соорентируем ее в направлении оси
, соорентируем ее в направлении оси  .
.
Положим, что в каждой точке этой поверхности задана непрерывная функция 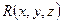 .
.
Определение: конечный предел интегральной суммы функции 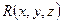 на поверхности
на поверхности  при условии, что
при условии, что 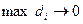 и
и  называется поверхностным интегралом по координатам
называется поверхностным интегралом по координатам 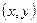 от функции
от функции 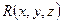 по поверхности
по поверхности  , где
, где 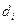 - диаметр частичной поверхности.
- диаметр частичной поверхности.
Т.о. 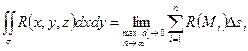 , где
, где 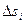 - величина полученной
- величина полученной
частичной проекции на 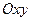 (число со знаком).
(число со знаком).
Аналогично, определяются поверхностные интегралы по координатам 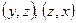 .
.
Составной поверхностный интеграл по координатам:
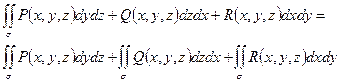
Основные свойства:
1) Каждый из поверхностных интегралов по координатам зависит от ориентации поверхности в направлении соответствующей оси, т.е.
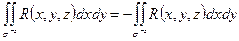
2) Если  - цилиндрическая поверхность с образующей, параллельной оси
- цилиндрическая поверхность с образующей, параллельной оси  , то
, то 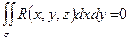 ;
;
|
|
|
3) Связь между поверхностными интегралами 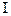 и
и 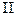 рода:
рода:
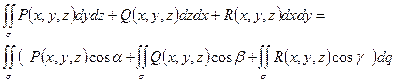 ,
,
где  - углы, образованные вектором
- углы, образованные вектором 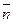 с соответствующими координатными осями.
с соответствующими координатными осями.
16.5. Вычисление поверхностного интеграла по координатам:
1) Выясняем, прямая параллельная какой оси, пересекает эту поверхность не более чем в одной точке;
2) Ориентируем поверхность в направлении этой оси;
3) Уравнение  разрешаем относительно этой переменной, проецируем
разрешаем относительно этой переменной, проецируем  на соответствующую двумерную плоскость.
на соответствующую двумерную плоскость.
4) Переходим к двойному интегралу:
|
|
|
|
|
Дата добавления: 2015-06-28; Просмотров: 396; Нарушение авторских прав?; Мы поможем в написании вашей работы!