Для аналитических 2 страница

Обозначение: 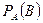или .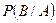

Определение: вероятность события 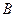, вычисленная без учета появления, или не появления называется безусловной вероятностью события .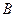

Обозначение: .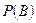

Теорема умножения:

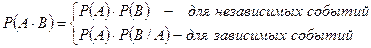
Замечание: теорема остается справедливой и для большего количества событий.

Определение: суммой двух событий и 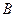называется событие, состоящее в том, что появится хотя бы одно из этих событий.

Обозначение: .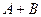

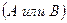Теорема сложения:

.

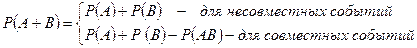Замечание: теорема остается справедливой и для большего количества событий.

Следствия:

- Сумма вероятностей несовместных событий, образующих полную группу, равна единице, т.е. ;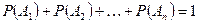

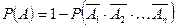- - формула расчета вероятности появления хотя бы одного из совместных событий.

Теорема (формула полной вероятности):

Если случайные гипотезы 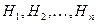образуют полную группу несовместных событий и событие может произойти только после наступления одной из гипотез, то вероятность появления события рассчитывается по формуле

.

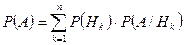Теорема (гипотез или формула Бейеса):

Пусть случайные гипотезы 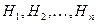образуют полную группу несовместных событий, известны вероятности появления этих гипотез 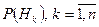, событие уже произошло, то .

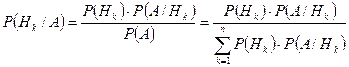Повторение испытаний:

- Если 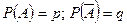, то ;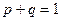

- В независимых испытаниях событие появится хотя бы один раз с вероятностью .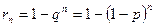

Теорема (формула Бернулли):

Если проводится независимых испытаний, в результате каждого из которых событие может появится с вероятностью 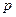и не появится с вероятностью 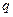,то вероятность того, что в испытаниях событие появится ровно 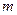раз рассчитывается по формуле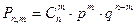

Эта формула целесообразна при небольших .

Теорема (локальная теорема Муавра-Лапласа):

Если вероятность 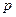появления события в результате каждого из независимых испытаний постоянна и отлична от 0 и 1, то при достаточно больших вероятность того, что в испытаниях событие появится ровно 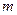раз имеет представление

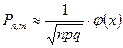, где .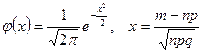

Функция 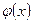- непрерывная и положительная при любых 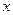, четная и .

.

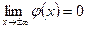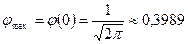При 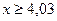полагают .

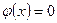Закон Пуассона:

Если достаточно велико, 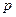- достаточно мало, то с наименьшей погрешностью

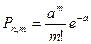, где .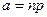

Интегральная теорема Лапласа:

Если вероятность 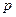появления события в результате каждого из независимых испытаний постоянна и отлична от нуля и единицы, то при достаточно больших вероятность того, что событие наступит от 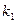до 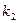раз имеет следующее представлени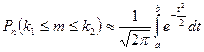е , где ; .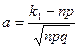

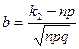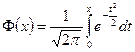- функция Лапласа.

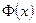- непрерывна при любых 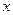, нечетная .

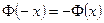При 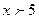полагают .

.

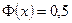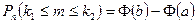6.4. Случайные величины:

Определение: случайной величиной называется величина, которая в результате ОКУ заведомо принимает одно и только одно из своих возможных числовых значений, причем заранее неизвестно какое именно.

Определение: случайная величина, возможные значения которой изолированы друг от друга называется дискретной (ДСВ).

Определение: случайная величина, возможные значения которой непрерывно заполняют некоторый интервал, конечный или бесконечный, называется непрерывной (НСВ).

Определение: всякое соответствие, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями называется законом распределения случайной величины.

Простейшей формой закона распределения ДСВ является ряд распределения, т.е. таблица, в которой перечислены все возможные значения случайной величины и соответствующие им вероятности, т.е.

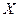
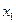
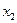
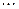
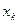
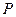
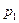
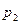
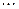
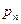
Где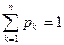

Определение: ломаная, соединяющая точки с координатами 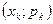, 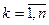называется многоугольником или полигоном распределения ДСВ.

Определение: возможное значение случайной величины, имеющее наибольшую вероятность, называется модой этой случайной величины.

Определение: функцией распределения 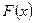случайной величины 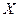называется вероятность того, что эта случайная величина примет значение меньшее, чем 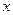, т.е. .

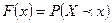Основные свойства :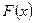

- значения функции распределения принадлежат отрезку ;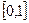

- функция распределения неубывающая;

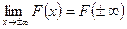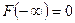- если , то и ;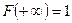

- если возможные значения НСВ принадлежат 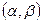, то при 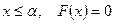, а при .

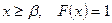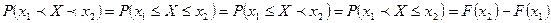- вероятность попадания НСВ в интервал любого типа.

Определение: предел средней плотности распределения вероятности НСВ в 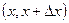, при условии, что длина этого интервала 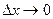, называется плотностью распределения вероятности данной случайной величины в точке .

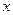Обозначение: .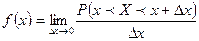

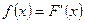для .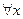

Теорема:

Вероятность попадания НСВ 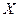в интервал 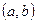равна определенному интервалу на соответствующем отрезке 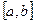от плотности распределения, т.е. .

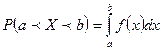Связь между функцией распределения и плотностью распределения НСВ:

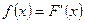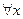для и .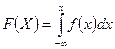

Свойства плотности распределения:

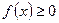- при ;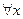

- ;

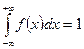6.5. Числовые характеристики случайных величин:

1) Математическое ожидание

Для дискретной случайной величины

Определение: сумма произведений всех возможных значений ДСВ на соответствующие им вероятности называется математическим ожиданием этой случайной величины.

Т.о. .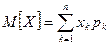

Математическое ожидание – константа, имеющая размерность случайной величины.

Математическое ожидание приближенно равно среднему арифметическому всех возможных значений данной случайной величины.

Свойства математического ожидания:

- ;

- ;

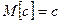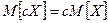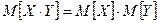- для независимых ДСВ;

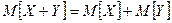- для независимых ДСВ;

- .

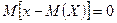Для непрерывной случайной величины

.

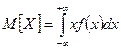Вероятностный смысл и свойства ДСВ остаются справедливыми.

2) Дисперсия

Определение: математическое ожидание квадрата отклонения случайной величины от своего математического ожидания называется дисперсией.

Т.о 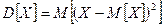или .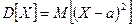

Дисперсия – константа, имеющая размерность квадрата случай величины.

Дисперсия характеризует степень разброса возможных значений случайной величины относительно ее центра, т.е. МО.

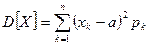- для ДСВ.

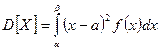- для НСВ.

Теорема: .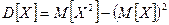

Свойства дисперсии:

- ;

- ;

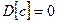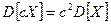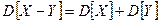- для независимых ДСВ;

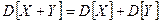- для независимых ДСВ.

3) Среднее квадратическое отклонение:

.

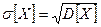СКО имеет размерность СВ, вероятностный смысл тот же, что и у .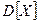

Теорема:

Если проводится независимых испытаний, в результате каждого из которых событие может появится в вероятностью 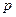и не появится с вероятностью 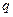, то , .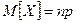

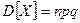4) Моменты распределения:

Определение: начальным моментом 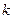- го порядка, называется математическое ожидание 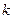- ой степени данной случайной величины т.е. 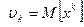, где

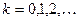
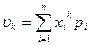- для ДСВ, заданной рядом распределения.

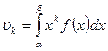- для НСВ с возможными значениями из 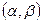и плотностью .

; ; .

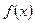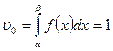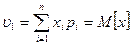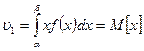Определение: центральным моментом 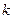- го порядка называется математическое ожидание 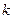- ой степени отклонения случайной величины от своего математического ожидания, т.е. 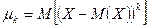, где

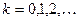
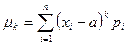- для ДСВ;

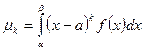- для НСВ.

; ; .

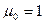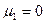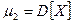5) Нормальный закон распределения:

Определение: НСВ плотность которой при всех 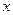значениях определяется равенством 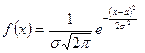, где 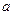- любое действительное число, 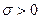называется распределенной по нормальному закону.

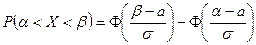- вероятность попадания нормально распределенной случайной величины в заданный интервал.

РАЗДЕЛ VII. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

7.1. Основные понятия:

Определение: множество всех объектов, подлежащих обследованию называют генеральной совокупностью.

Определение: множество объектов случайным образом отобранных из генеральной совокупности называют выборочной совокупностью или выборкой.

Определение: количество объектов совокупности генеральной или выборочной называют объемом этой совокупности.

Определение: перечень вариант (наблюдаемых значений 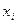) и соответствующих им частот 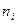(число наблюдений) или частостей 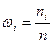называют статистическим рядом распределения выборки, где - объем выборки.

Его вид: , .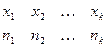

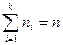Определение: разность между минимальной и максимальной вариантами называют размахом вариации.

Определение: варианта, имеющая максимальную частоту, называется модой вариации.

Определение: число, разделяющее вариационный ряд на две части, равные между собой по количеству вариант, называют медианой вариации.

Статистический ряд распределения допускает геометрическое изображение:

Полигон (ломаная, соединяющая точки 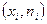, 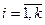) для дискретного случая и гистограмма (ступенчатая фигура – совокупность прямоугольников с основанием 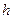и высотами 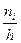) для непрерывного случая.

Определение: статистической функцией распределения выборки 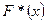называется функция, определяющая для каждого значения 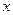относительную частоту события .

.

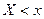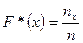Свойства :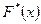

1) ;

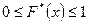2) 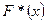- неубывающая функция.

3) Если 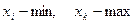варианты, то при .

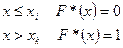7.2. Числовые характеристики генеральной и выборочной совокупностей:

Определение: среднее арифметическое всех возможных значений выборки называется выборочной средней величиной, т.о. .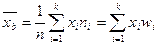

Определение: среднее арифметическое квадратов отклонений вариант от выборочной средней называется выборочной дисперсией,

т.о. .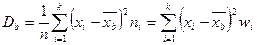

.

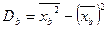Выборочное среднее квадратическое отклонение: .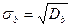

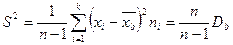- исправленная выборочная дисперсия.

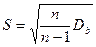- исправленное выборочное СКО.

7.3. Доверительный интервал для параметров нормального распределения:

1) 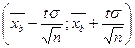-доверительный интервал для параметра 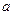при заданной ;

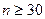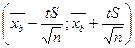2)Если , то -доверительный интервал для параметра 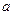при неизвестном ;

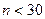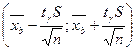Если , то -доверительный интервал для параметра 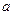при неизвестном , где .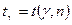

3) Доверительный интервал для параметра :

Если 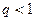, то доверительный интервал имеет вид .

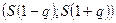Если 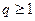, то доверительный интервал имеет вид 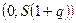, где .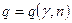

7.4. Статистическая проверка гипотез:

Определение:

Статистической гипотезой называется всякое высказывание о генеральной совокупности проверяемое по выборке.

Критерий Пирсона.

1. Выдвигается основная гипотеза 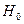относительно закона распределения данной генеральной совокупности и ей альтернативная .

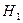2. Из генеральной совокупности извлекается случайная выборка и по ней составляется допустимый 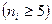статистический ряд распределения.

3. Вычисляем по данным выборки параметры предполагаемого распределения генеральной совокупности.

4. Находят вероятности 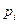попадания с.в. 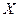в каждую частичную область, после чего составляют гипотетический ряд распределения выборки.

5. По формуле 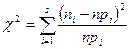находят значение .

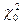Дата добавления: 2015-06-28