Парабола

I Каноническое уравнение параболы

Определение 1. Параболой называется линия, которая в некоторой ДПСК имеет уравнение

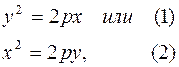
где p – некоторое положительное число.

Рассмотрим параболу (1). Т.к. замена y на (–y) не изменяет уравнения, это означает симметрию линии относительно оси Ox. В верхней полуплоскости уравнение (1) равносильно уравнению

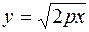. (3)

При x< 0 корень не существует, следовательно, левее оси ординат ни одной точки параболы (1) нет. При x= 0 получаем y= 0: начало координат является самой “левой” точкой параболы (1) и с возрастанием x от 0 до

y возрастает аналогично. Методы математического анализа позволяют выяснить, что линия (3) выпукла вверх и в начале координат касается оси ординат. Асимптот у параболы нет.

II Определяющее свойство параболы

Для параболы (1) рассмотрим точку 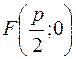, которую назовем фокусом параболы, и прямую 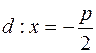, которую назовем директрисой. И пусть точка M (x, y)–произвольная точка параболы (1) т.е. x≥ 0,а y ² = 2 px. Найдем расстояние от M до F и до d:

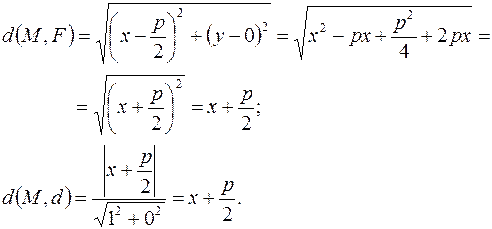
Итак, точки параболы равноудалены от фокуса и директрисы.

Это свойство (как и в случае эллипса и гиперболы) можно взять в качестве определения.

Определение 2. Парабола есть геометрическое место точек (плоскости) равноудаленных от данной точки (называемой фокусом) и данной прямой (называемой директрисой).

Исходя из этого определения, получим каноническое уравнение, для чего обозначим расстояние от фокуса F до директрисы d через p, а ДПСК выберем следующим образом: ось абсцисс проведем через фокус перпендикулярно к директрисе и будем считать ее направленной к фокусу от директрисы, а начало координат поместим посередине между F и d. В этой системе: 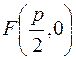и 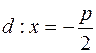. Пусть теперь M (x, y) текущая точка параболы (определение 2). Заметим сразу, что M не может находиться левее оси ординат, ибо в этом случае d (M, F) >d (M, d). Найдем эти расстояния:

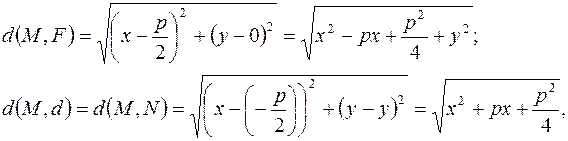
здесь 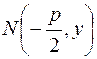– проекция M на директрису. Приравняем (в соответствии с определением 2) полученные расстояния и для упрощения возведем обе части полученного равенства в квадрат (посторонние корни не появятся; почему?). После упрощения получим каноническое уравнение (1): y²=2px.

Замечание 1. Уравнение (2) получим, если ось Oy провести через F перпендикулярно к d и от d к F. Кроме уравнений (1) и (2) рассматривают еще два уравнения y²= – 2 px – ось Ox направлена от F к d, и x²= –2 py – ось Oy направлена от F к d.

III Элементы параболы

Ось симметрии – это просто ось параболы. Точка пересечения параболы со своей осью – это вершина параболы. Если M – точка параболы, то отрезок MF и его длина r называется фокальным радиусом точки M. Очевидно, что для параболы (1) 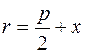. К элементам параболы относят также фокус и директрису.

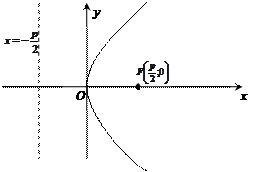Замечание 2. Параметр параболы p имеет еще один наглядный смысл. Проведем че- рез фокус прямую, перпендикулярную к оси параболы и пусть M и N –это точки пересечения прямой с параболой. Тогда

.

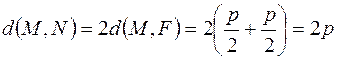Таким образом, p характеризует “ширину” области, ограниченной параболой (при

условии, что эта ширина измеряется перпендикулярно к оси на определенном расстоянии от вершины).

IV Нормальное уравнение параболы

Если вершина параболы имеет координаты (x ₀, y ₀), а ось параллельна оси Ox, то ее уравнение имеет вид:

.

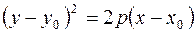Если же ось параллельна Oy, то

.

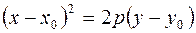Типовые задачи. 1). Составить каноническое уравнение параболы, зная некоторые ее элементы. 2). От общего уравнения y ² + 8 x– 6 y– 7=0 перейти к нормальному и найти элементы параболы. 3). Исходя из определения 2, найти уравнение параболы, у которой фокус F (1;1), а уравнение директрисы x+y+ 2=0. (Заметим, что при решении этой задачи получим общее уравнение, в котором присутствует член, содержащий произведения переменных, из-за того, что ось параболы не параллельна ни одной из координатных осей).

§6. Касательные к кривым 2^го порядка

I Определения

Касательную к окружности, эллипсу, гиперболе и параболе можно определить как прямую, имеющую с кривой одну общую точку, за исключением двух случаев: 1) прямая, параллельная асимптоте гиперболы, пересекает ее в одной точке, но не является касательной; 2) прямая, параллельная оси параболы, пересекает параболу в одной точке, но не является касательной.

Касательную к окружности можно определить и как прямую, проходящую через точку окружности перпендикулярно к радиусу, проведенному в эту точку.

II Уравнения касательных

Методами математического анализа можно получить (нужно уметь!) уравнения касательных к линиям, заданными своими каноническими уравнениями. Пусть точка (x ₀, y ₀) лежит на линии. Тогда:

1) касательная к эллипсу 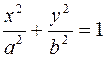имеет вид ;

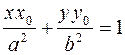2) касательная к гиперболе 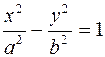имеет вид ;

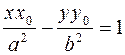3) касательная к параболе y ² = 2 px имеет вид y ₀ y=p (x+x ₀).

Замечание. Окружность понимаем как частный случай эллипса.

III Некоторые свойства касательных

1. Фокусы эллипса расположены по одну сторону от любой его касательной, а фокусы гиперболы – по разные стороны.

2. Фокальные радиусы любой точки эллипса (гиперболы) образуют равные углы с касательной, проходящей через эту точку.

3. Произведение расстояний от фокусов эллипса (гиперболы) до любой касательной к линии есть величина постоянная.

4. Отрезок касательной к гиперболе, заключенный между ее асимптотами, делится пополам точкой касания.

5. Площадь треугольника, образованного касательной к гиперболе и ее асимптотами, есть величина постоянная.

6. Касательная к параболе в любой ее точке образует равные углы с фокальным радиусом этой точки и лучом, исходящим из нее и идущим параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.

7. Касательные к эллипсу (гиперболе), проведенные в концах одного и того же диаметра, параллельны.

Дата добавления: 2015-06-28