Примеры построения эпюр поперечной

ИЗГИБЕ

ЛИНЕЙНЫЕ И УГЛОВЫЕ ПЕРЕМЕЩЕНИЯ ПРИ ПЛОСКОМ

В ряде случаев работающие на изгиб элементы машиностроительных и строительных конструкций должны быть рассчитаны не только на проч­ность но и на жесткость. Под действием внешних нагрузок сечения балки перемещаются в вертикальном направлении и поворачиваются вокруг ней­тральной оси. В силу малости деформации (деформации упругие) прини­мается, что сечения перемещаются перпендикулярно оси балки и остаются плоскими после поворота. Вертикальные перемещения сечений балки на­зывают прогибами у, поворот сечений - углом поворота . Искривленная ось балки после деформации называется упругой линией балки (рис. 4.).

Упругую линию балки можно рассматривать как график некоторой
функции, определяемой характером нагружения балки, ее размерами и ма­
териалом.

Приближенное дифференциальное уравнение упругой балки постоян­ного сечения записывается в следующем виде:

(9)

Здесь M_z - уравнение изгибающих моментов, как аналитическое выра­жение закона изменения изгибающего момента по длине балки.

Для определения углов поворота и прогибов необходимо проинтегри­ровать левую и правую части уравнения (9):

Рис. 4. К определению прогибов, углов поворота и упругой линии балки при плоском изгибе.

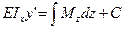- уравнение углов поворота (10)

Интегрируем второй раз:

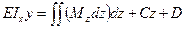- уравнение упругой линии балки. (11)

Постоянные интегрирования С и D определяются из граничных условий

на балке. Отметим, что - представляют собой угол

поворота 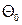и прогиб С₀ в начале координат.

Порядок интегрирования дифференциального уравнения показан на примере балки на рис. 4. При составлении уравнения изгибающего момен­та и порядка интегрирования необходимо выполнение следующих усло­вий, предложенных Бубновым-Клебшем::

1. Отсчет абсцисс z производить от одного начала координат.

2. Сосредоточенный момент должен иметь множитель-скобку M(z-c)⁰, в нулевой степени; где с - расстояние от начала координат до сечения, где приложен момент.

3. Момент от сосредоточенной нагрузки должен иметь множитель-скобку (z-d)¹, где d - расстояние от начала координат до сечения, где приложе­на сосредоточенная сила.

4. Распределенная нагрузка начавшись на балке, не должна прерываться. Ее нужно продлить до конца балки, а добавленный участок нагрузки компенсировать нагрузкой, направленной в противоположную сторону от добавленной.

5. Интегрирование необходимо вести без раскрытия скобок.

6. При соблюдении вышеуказанных условий при интегрировании диффе­ренциального уравнения определяется только две постоянных интегри­рования.

Следуя указанным условиям дифференциальное уравнение, для рас­сматриваемой балки (рис.4) примет вид:

В соответствии с формулой (9) приближенное дифференциальное урав­нение упругой линии балки (рис. 4) примет вид:

(12)

Проинтегрировав уравнение (12) один раз получим уравнение углов поворота:

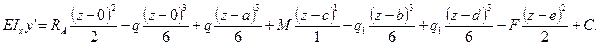(13)

Проинтегрировав уравнение (12) дважды получим уравнение прогибов:

(14)

Произвольные интегрирования С и D определяются из граничных усло­вий на балке:

1. 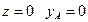; отсюда D=0, так как - прогиб в начале координат.

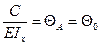2. отсюда определяем C: - угол в начале координат.

Значение С подставляется в уравнения (13) и (14), затем вычисляются значения прогибов у и углов поворота по длине балки.

Условие жесткости балки по линейным перемещениям имеет вид:

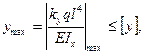(15)

где у_mах - максимальный прогиб; к_у - коэффициент, определяемый с эпюры прогибов у; [у] - допускаемый прогиб балки, обычно рекомендует­ся [у]=(0,001…0,002)L, где L-длина балки.

Условие жесткости по угловым перемещениям имеет вид:

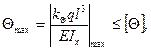(16)

где 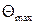- максимальный угол поворота сечений балки; 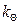- коэффици­ент, определяемый с эпюры углов поворота; 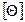- допускаемый угол пово­рота балки.

Если прочность балки обеспечена, а условие жесткости не выполняется, то задача решается из условия жесткости.

(ПЕРЕРЕЗЫВАЮЩЕЙ) СИЛЫ Q_y И ИЗГИБАЮЩЕГО МОМЕНТА М_х

Дата добавления: 2015-06-29