Систематизация Эйлером дифференциального и интегрального исчисления

Соединение шплинтовое

Стопорные шайбы и шплинты предотвращают самоотвинчивание болтов и гаек при вибрациях и ударах.

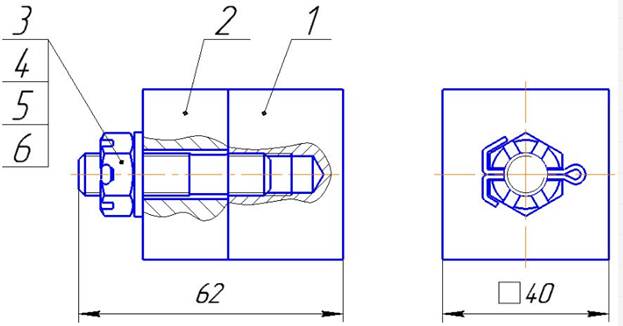
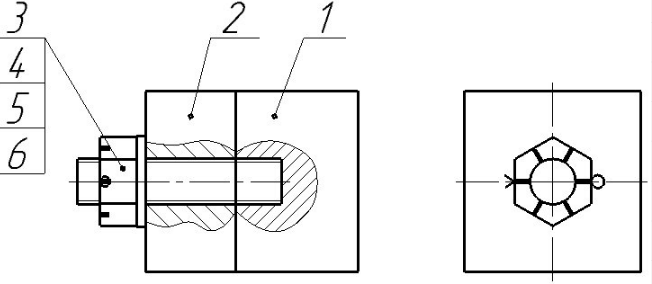
Упрощенное изображение:

Научные труды Л. Эйлера до сих пор поражают нас не только оригинальностью рассуждений, но и, что очень значимо, методическим мастерством. Недаром Лаплас говорил: «Читайте, читайте Эйлера - это учитель нас всех», а «король математиков» Гаусс писал: «Изучение работ Эйлера остаётся наилучшей школой в различных областях математики, и ничто другое не может это заменить».

Первые курсы исчисления бесконечно малых написаны в конце XVII века Г. Лопиталем («Анализ бесконечно малых», 1696) и И. Бернулли («Лекции по интегральному исчислению», 1692). Но, так как уже в первой трети XVIII века было накоплено много нового, то необходимо было систематизировать все новое содержание математического анализа.

Заслуга в решении этой задачей исключительной широты и сложности принадлежит Л. Эйлеру, труды которого, опубликованные в 1748-1770 гг., составили эпоху не только в МА, но и в математике в целом. К ним относятся 2 тома «Введения в анализ бесконечных», 2 книги «Дифференциального исчисления» и 3 тома «Интегрального исчисления» - эта трилогия является энциклопедией МА того времени, влияние этих трудов на дальнейшее развитие МА и его приложений переоценить невозможно.

«Введение в анализ бесконечных» (1748):

в I томе Эйлер:

· определяет предмет МА: «Весь анализ бесконечных величин заключается в исследовании переменных величин и их функций»;

· развивая учение о функции, даёт сразу необходимые вычислительные средства, основными из которых являются разложения

ü в обобщённые степенные ряды,

ü бесконечные произведения.

ü непрерывные дроби;

· рассматривает общую классификацию функций, в основном сохранённую в современном анализе (алгебраические и трансцендентные функции);

· даёт классическое построение теории трансцендентных функций, в частности излагает:

ü теорию логарифмов комплексных переменных,

ü формулы Муавра в современном виде,

ü формулы Эйлера, связывающие экспоненту и тригонометрические функции (появившиеся ещё в 1741 г. в переписке с Х. Гольдбахом);

ü указывает один из самых действенных способов изучений трансцендентных функций – разложение их в ряды, рассматривая 2 способа – арифметический (члены ряда – числа и требуется сходимость ряда) и алгебраический (бесконечный ряд – формальной выражение, порождённое заданной функцией, и может быть расходящимся);

ü с помощью расходящихся рядов находит разложение гамма-функции в произведение, а также функциональные уравнения гамма- и дзета-функции;

во II томе:

· кратко изложены геометрические приложения математического анализа, т.е. аналитическая геометрия на плоскости:

ü рассмотрены кривые, заданные на разных кусках интервала определения различными аналитическими выражениями,

ü дана классификация кривых и соответствующих им функций,

ü выводятся формулы преобразования координат,

ü изучается общее уравнение прямой,

ü выясняется число точек пересечения алгебраической кривой n-го порядка с прямой,

ü излагается теория конических сечений (3-х классов),

ü определяются и изучаются асимптоты (прямая или более простая кривая, которая на бесконечности сливается с рассматриваемой кривой),

ü определена касательная, как прямая или более простая кривая, которая совпадала бы на очень маленьком протяжении с некоторой частью рассматриваемой кривой,

ü исследованы вопросы о радиусе круга кривизны, об особых точках, точках перегиба,

ü особое внимание уделено изучению обратных тригонометрических функций и различного вида спиралей,

· «Приложение о поверхностях» - это первое систематическое изложение аналитической геометрии в пространстве:

ü исследованы поверхности с помощью плоских сечений,

ü выведены общие формулы преобразования пространственных координат с помощью «эйлеровых углов»,

ü исследовано общее уравнение второго порядка с тремя переменными (выделены 6 конических видов поверхностей второго порядка).

В 1755 году Петербургская академия наук опубликовала «Дифференциальное исчисление» Эйлера. По содержанию, систематичности изложения и последовательности в развитии новых понятий и алгоритмов это сочинение можно поставить на одно из самых почётных мест во всей истории математического анализа. Весьма сильное влияние оно оказало на развитие и преподавание математики в России.

В первой половине XVIII века назрела необходимость освободить основания нового исчисления от геометрической и механической трактовки, т.е. излагать его аналитическим методом, что и сделано Эйлером в его «Дифференциальном исчислении». Книга состоит из 2 частей, в 1-ой из которых излагается дифференциальное исчисление в собственном смысле слова, во 2-ой – применение ДИ, теории рядов и непрерывных дробей к решению алгебраических уравнений, нахождению точек минимума и максимума функции одного и двух аргументов. Вопросам приложения ДИ к геометрии Эйлер планировал посвятить 3-ю часть, которую так и не написал.

В течение 1768-1770 гг. (каждый год по тому) было издано «Интегральное исчисление» Эйлера – сочинение с необычайным богатством новых результатов, содержащее сложные вопросы теории ОДУ и ДУ в частных производных. Без преувеличения можно сказать, что оно составило новую эпоху в развитии математического анализа. Так как в понятие интегрального исчисления Эйлер, как и все его современники, включал не только интегрирование функций, но и ДУ, то содержание томов было таково:

Два тома содержали 4 раздела:

· интегрирование функций (I том, ч. 1),

· интегрирование ОДУ I порядка (I том, ч. 2),

· интегрирование ДУ второго и высшего порядков (II том, ч. 1),

· интегрирование уравнений с частными производными (II том, ч. 2).

В 1794 году Петербургская академия наук издала IV (посмертный) том «Интегрального исчисления» Эйлера, в котором были собраны все дополнения к предыдущим томам.

Таким образом, изданием этих фундаментальных эйлеровских трудов был подведён итог открытиям мировой математики в области математического анализа, включая ДУ, специальные функции, вариационное исчисление, элементы теории аналитических функций и другие разделы математики, получившие впоследствии самостоятельное развитие.

5. Развитие теории дифференциальных уравнений

а) Основные направления развития теории ОДУ в XVIII веке

1) Первые же задачи динамики точки, сформулированные аналитически, потребовали методов интегрирования нелинейных уравнений второго порядка и их систем. В частности к нелинейным уравнениям второго порядка привело важное для практических приложений нахождение геодезических линий на поверхности.

2) Все более серьёзное значение в механике приобретала теория малых колебаний материальных систем с конечным числом степеней свободы, а для её дальнейшего развития было необходимо развитие теории линейных ДУ. Методов решения ЛДУ и их систем требовали и теории построения маятников, теория колебания струны и изучение распространения звука.

3) Такое направление теории ОДУ, как численные методы приближенного интегрирования ДУ, было обусловлено требованиями небесной механики. Часто решение проблемы приводило к уравнениям и их системам, неинтегрируемым в конечном виде.

4) Задачи быстроразвивающейся дифференциальной геометрии нуждались в изучении особых решений ДУ, главнейшими из которых были задачи о нахождении огибающих и изогональных траекторий семейств кривых. (Линии, пересекающие все кривые данного семейства под одним и тем же углом φ, называются изогональными траекториями).

Итак, уровень накопленных к началу XVIII века о свойствах и способах решений ОДУ был совершенно недостаточен для исследования новых проблем, поэтому уже со второй четверти столетия наблюдалось значительное повышение интереса к этой области. Например, в первом же томе «Комментариев» Петербургской АН (1726 г.) были помещены статьи Я. Германа, Х. Гольдбаха, И. Бернулли, его сыновей Николая и Даниила. Весьма значительное развитие в XVIII столетии теория ОДУ получила в трудах Эйлера, братьев Бернулли, Даламбера, Лагранжа, Лапласа.

Отметим сначала, что у математиков того времени задача интегрирования ОДУ ставилась как задача нахождения полного (общего) интеграла, а необходимое частное решение выделялось потом с помощью некоторого выбора значений произвольных постоянных, соответствующих в подавляющем большинстве случаев постановке задачи с начальными условиями.

б) Методы интегрирования нелинейных ОДУ

Из нелинейных ДУ Эйлера более всего привлекало уравнение Риккати в его различных формах, причём интерес к нему был связан, не столько в связи с задачами механики и геометрии, сколько с рядом вопросов гидравлики и колебания неоднородной струны, появившихся в зоне его интересов. Из множества нелинейных уравнений Эйлер в результате выделил довольно широкий класс уравнений, названных им «однородными». Кроме того, им были исследованы более общие уравнения высших порядков, чем уравнения Лагранжа, соответственно обобщив прием интегрирования исходного уравнения по независимому переменному.

Охарактеризуем вкратце достижения Эйлера в этой области:

· Интегрирование уравнения Риккати с помощью непрерывных дробей.

Первым непрерывные дроби к интегрированию ДУ применил Лагранж. Две самые ранние работы Эйлера по теме относятся к 1737-1739 году, но опубликованы значительно позже. В них Эйлер рассмотрел широкий круг вопросов:

ü развитие ряда алгоритмов, связанных с непрерывными дробями,

ü суммирование бесконечных рядов с помощью непрерывных дробей,

ü применение непрерывных дробей при решении вопросов итерационного исчисления и приближённого решения алгебраических уравнений. методы суммирования непрерывных дробей некоторого частного вида,

ü сведение задачи суммирования непрерывной дроби к интегрированию соответствующего уравнения Риккати.

· Методы понижения порядка.

Интегрирование нелинейных уравнений, как известно, представляет большие трудности, более или менее полная теория развита только для некоторых классов таких уравнений. У Эйлера задача понижения порядка решена для 4 типов уравнений:

1.;

2.;

3.;

4., причём новыми оригинальнейшими методами.

· Метод интегрирующего множителя.

В работе «О дифференциальных уравнениях второго порядка» Эйлер впервые в теории ДУ поставил задачу о частичном интегрировании уравнений второго порядка, т.е. задачу (в современной терминологии) нахождения первых интегралов, и для её решения использовал метод интегрирующего множителя. Основное содержание работы:

ü указание общих форм ДУ различных порядков, допускающих интегрирующие множители,

ü попытка классификации интегрирующих множителей,

ü нахождение первых интегралов с помощью различных интегрирующих множителей.

Для примера, Эйлер нашёл для уравнения

интегрирующий множитель

(при имеется множитель не 2-го, а 1-го порядка).

в) Теория линейных дифференциальных уравнений

До работ Эйлера изучены, в основном, были только ЛДУ 1-го порядка. Исследования Эйлера в этой области представлены четырьмя циклами работ:

1 цикл - работы, содержащие решения разнообразных линейных задач механики и физики, большая часть этих исследований приходятся на 1725-1750 гг.:

ü особое внимание отведено проблеме малых колебаний механических систем с конечным числом степеней свободы;

ü впервые даны аналитические методы динамики точки. в частности рассмотрены колебательные движения в среде с сопротивлением («Механика», т.1-2, 1736);

ü опубликована серия работ о колебаниях сложных маятников, тяжелой нити, приливах и отливах, распространении колебаний в упругой среде.

В этих работах Эйлер пришёл не только к методам интегрирования однородных и неоднородных уравнений второго порядка, но и линейных систем ДУ с постоянными коэффициентами.

2 цикл – первые теоретические работы о линейных уравнениях с переменными коэффициентами (до 1743 г.).

3 цикл – специальные работы о линейных уравнений с постоянными коэффициентами. Это, в основном, две работы: «Об интегрировании дифференциальных уравнений высших порядков» и «О распространении колебаний упругой среды».

4 цикл - дальнейшее развитие теории ЛДУ с переменными коэффициентами. Этот цикл начинается мемуаром «Метод дифференциальных уравнений высших порядков» и заканчивается работами о сопряжённых уравнениях, представляющими собой развитие результатов Лагранжа.

г) Методы приближенного решения ДУ

В работах Эйлера по небесной механике получил дальнейшее развитие метод бесконечных рядов. Создание методов приближенного анализа стимулировала и математическая физика. Классическими методами того времени являлись:

ü разложение в степенной ряд. Для многих типов дифференциальных уравнений не может быть найдено точное аналитическое решение. В этом случае дифференциальное уравнение можно решить с помощью приближенных методов, и, в частности, с помощью разложения в степенной ряд неизвестной функции.

ü метод ломаных - численный метод решения (систем) ОДУ («Интегральное исчисление» (1768)), основанный на аппроксимации интегральной кривой кусочно-линейной функцией, т. н. ломаной Эйлера.

ü Необходимость решения вопросов теоретической астрономии и математической физики привели его к применению для приближенного решения ДУ тригонометрических рядов. В мемуаре «Простой метод получения рядов…» (1793 г.) он писал, что в теоретической астрономии все аналитические выражения представляются такими рядами, члены которых суть синусы или косинусы кратных углов и указал виды таких рядов для изучения регулярного и нерегулярного движения планет. Кроме того, в одном из мемуаров по вопросу определения коэффициентов тригонометрических разложений он сначала открыл способ их приближенного вычисления, основанный на идее тригонометрического интерполирования, а потом и способ интегрального их представления (совпадающий с современным).

д) Теория ДУ в частных производных

Дифференциальные уравнения в частных производных представляют собой одну из наиболее сложных и одновременно интересных задач вычислительной математики. Эти уравнения характеризуются тем, что для их решения не существует единого универсального алгоритма, и большинство задач требует своего собственного особого подхода. Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.).

Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных, например или. Постановка задач включает в себя само уравнение (или систему уравнений), содержащее производные неизвестной функции по различным переменным (частные производные), а также определенное количество краевых условий на границах расчетной области. Сами уравнения в частных производных несколько условно можно разделить на три основных типа:

· параболические - содержащие первую производную по одной переменной и вторую - по другой, причем все эти производные входят в уравнение с одинаковым знаком;

· гиперболические - содержащие первую производную по одной переменной и вторую - по другой, входящие в уравнение с разными знаками;

· эллиптические - содержащие только вторые производные, причем одного знака.

Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.

Первое уравнение в частных производных историки обнаружили в статьях Эйлера по теории поверхностей, относящихся к 1734-1735 годам (опубликованы в 1740 году). В современных обозначениях оно имело вид:. В тех же работах имеется и первая постановка задачи о решении уравнения с частными производными первого порядка, правда, ещё не совсем чёткая. Она связана с изучением задач геометрии и развитием метода интегрирующего множителя.

Начиная с 1743 года, к работам Эйлера присоединился Даламбер, предложивший общее решение волнового уравнения для колебаний струны в виде суммы 2 произвольных функций, определяемых по начальным и граничным условиям, где - длина струны. В последующие годы Эйлер и Даламбер опубликовали ряд методов и приёмов для исследования и решения некоторых уравнений в частных производных. В частности, они разошлись во мнениях о природе допустимых функций, входящих в решение уравнений с частными производными, в этот научный спор были вовлечены почти все крупные математики нескольких поколений, что существенно повлияло как на интерес к теме, так и на дальнейшее развитие теории ДУ в ЧП.

В 60-х годах в ряде работ Эйлер устанавливает связь между задачами интегрирования уравнений и теорией уравнений в полных дифференциалах, что дало ему возможность в новой области опереться на прежние свои результаты в области теории ОДУ. Развивая метод интегрирования отдельных классов уравнений в ЧП, он использует методы решения уравнений в полных дифференциалах, в частности метод интегрирующего множителя.

В 1755 году публикуются «Общие принципы движения жидкостей» Эйлера, в которых положено начало теоретической гидродинамике, выведены основные уравнения гидродинамики (уравнение Эйлера) для жидкости без вязкости, разобраны решения системы для разных частных случаев. Основные результаты Эйлера в области интегрирования уравнений математической физики (задачи о колебании струны, пластинки, мембраны) стимулировали развитие теории ДУЧП и обеспечивал отправную точку для открытий других ученых Лагранжа, Лапласа и пр., но ещё не создали завершённой теории.

6. Исследования Эйлера по вариационному исчислению.

Вариационное исчисление - раздел функционального анализа, самая типичная задача которого состоит в том, чтобы найти функцию, на которой заданный функционал достигает экстремального значения.

Методы вариационного исчисления широко применяются в различных областях математики:

· в дифференциальной геометрии с их помощью ищут геодезические линии и минимальные поверхности;

· в физике вариационный метод - одно из мощнейших орудий получения уравнений движения;

· методы вариационного исчисления применимы в статике.

Типичными примерами вариационной задачи являются изопериметрические задачи в геометрии и механике, в частности, задача о брахистохроне, задача нахождения уравнений поля из заданного вида действия для этого поля.

В 1744 году Эйлер открывает вариационное исчисление, в его работах используются продуманная терминология и математическая символика, в значительной степени сохранившиеся до наших дней, изложение доводится до уровня практических алгоритмов.
Эйлеру принадлежит и сам термин (1766 год). Эйлеровский алгоритм затем блестяще развил Лагранж, что было очень высоко оценено самим Эйлером.

К концу XVIII века класс решенных вариационных задач значительно расширился,
Эйлер и Лагранж изучили экстремальные свойства пространственных кривых и поверхностей.

7. Работы Эйлера по геометрии.

Всего у Эйлера 75 работ по геометрии, они занимают 3 тома «Opera omnia» - полного собрания его сочинений:

· Эйлер - один из зачинателей исследований по геометрии в пространстве, он первый во «Введении в анализ» дал связное изложение аналитической геометрии в пространстве и, в частности, ввел так называемые углы Эйлера, позволяющие изучать повороты тела вокруг точки.

· Эйлера можно считать основоположником топологии. В работе 1752 года «Доказательство некоторых замечательных свойств, которым подчинены тела, ограниченные плоскими гранями», Эйлер дал доказательство того, что у выпуклого многогранника с В вершин, Р ребер и Г граней эти числа всегда связаны соотношениями В — Р + Г = 2. Это первая в истории математики крупная теорема топологии, изучающей свойства фигур, не меняющиеся, если фигуру можно как угодно растягивать, сжимать и изгибать (но не склеивать и не рвать).

· Топологический характер носит и решённая Эйлером задача о кёнигсбергских мостах, а также – о ходе конём (1766) (разместить в 64 клетках 64 числа от 1 до 64 так, чтобы любые две клетки, содержащие последовательные числа, были связаны ходом коня).

· В работе «Исследование о кривизне поверхностей» (1760 год) Эйлер рассматривает вопрос, до того никем подробно не изучавшийся, находит простую формулу для радиуса кривизны любого нормального сечения.

· Работа 1769 года «Об ортогональных траекториях» Эйлера содержит блестящие соображения о получении с помощью ФКП из уравнений двух взаимно ортогональных семейств кривых на поверхности (т. е. таких линий, как меридианы и параллели на сфере) бесконечного числа других взаимно ортогональных семейств.

· В следующей работе 1771 года «О телах, поверхность которых может быть развернута в плоскость» Эйлер доказывает знаменитую теорему:

любая поверхность, которую можно получить, лишь изгибая плоскость, но не растягивая ее и не сжимая, если она не коническая и не цилиндрическая, представляет собой совокупность касательных к некоторой пространственной кривой (ее ребру возврата).

· Весьма существенен вклад Эйлера в развитие теории геометрических преобразований, он рассматривал преобразования координат, преобразования подобия, аффинные преобразования, движения и симметрии на плоскости, в пространстве, движения твёрдых и жёстких тел.

· Исследовал Эйлер и конформные отображения, в частности, круговые, совпадающие с дробно-линейными. В «Рассуждениях об ортогональных траекториях» Эйлер сделал множество открытий по конформным отображениям и блестяще применил их в ряде своих работ по картографии.

· работы Эйлера в области сферической геометрии явились первыми исследованиями внутренней геометрии кривой поверхности. Они, а также его исследования по сферической геометрии оказали несомненное влияние на Лобачевского.

В заключение описания геометрических работ Эйлера приведём слова немецкого математика Коммереля: «Слава и заслуги Гаусса не пострадают, если мы укажем на то, что ряд мыслей и методов, которые Гаусс так блестяще использовал …, имеется уже у Эйлера. Речь идет, например,

о сферическом отображении (когда куску поверхности ставится в соответствие кусок сферы радиуса 1, состоящий из всех таких точек, в которых радиусы этой сферы параллельны нормалям к поверхности в точках этого ее куска),

о задании поверхности в параметрической форме, совпадении линейных элементов как условии наложимости при изгибании,

об исследовании геодезических линий (т. е. кратчайших линий на поверхности между двумя ее точками) при помощи угла, который они образуют с кривыми некоторого семейства на поверхности, и другие».

8. Теоретико-числовые мемуары Эйлера

Все работы Эйлера по теории чисел (около 150 работ) поражают своей глубиной и оригинальностью. Именно с его именем связано становление теории чисел как науки:

· Разложив на множители натуральное число

,

он опроверг гипотезу Ферма, предполагавшего, что все числа вида - простые.

· Эйлер установил, что все совершенные чётные числа имеют вид, где и число Мерсенна - простые, и доказал, что число Мерсенна - простое. Заметим, что нечётных совершенных чисел до сих пор не найдено (Совершенное число – число, равное сумме всех своих собственных делителей).

· Ещё пифагорейцам была известна пара дружественных чисел: (220 и 284), Ферма обнаружил вторую пару: (17 296 и 18 416), Декарт – третью: (9 363 584 и 9 437 056). Эйлер же составил список 62 пар таких чисел, утвердив славу непревзойдённого никем вычислителя.

· Имя Эйлера носит введённая и исследованная им функция -количество натуральных чисел. меньших и взаимно простых с при. Эта функция играет важную роль в теории чисел. Используя её, Эйлер ввёл понятие первообразного корня по модулю - такого числа, что делится на тогда и только тогда, когда кратно, и доказал существование первообразного корня по любому простому.

· Подлинными жемчужинами теории чисел являются:

ü доказанные Эйлером теоремы о простых числах:

и - количество простых чисел, не больших;

ü его таблица 65 компанейских (подходящих) чисел (компанейскими называется такая группа из k чисел, в которых сумма собственных делителей первого числа равна второму, сумма собственных делителей второго – третьему и т.д., а первое число равно сумме собственных делителей k-го числа);

ü открытый им закон квадратичной взаимности

, где и - различные нечётные простые числа;

ü его многочлены, определяющие соответственно при только простые числа.

· Сформулированная Эйлером гипотеза, что всякое чётное число есть сумма двух простых чисел и гипотеза Гольдбаха о представлении всякого натурального числа в виде суммы трёх простых чисел составили знаменитую проблему Гольдбаха-Эйлера, не решённую полностью до сих пор.

· Хотя предложенное Эйлером доказательство основной теоремы алгебры (о существовании действительного или мнимого корня у любого многочлена степени с действительными коэффициентами) и не было достаточно обоснованным, оно содействовало появлению строгого доказательства Гаусса и других математиков.

9. Элементы теории вероятностей в работах Эйлера

К середине XYIII века ТВ начали чаще применять в демографии, страховании, оценке ошибок наблюдения, проведении лотерей и пр. Многие математики приняли участие в разработке вероятностных идей, в том числе и Л. Эйлер. Часть работ Эйлера опубликованы при его жизни, но большинство – посмертно, а некоторые – значительно позже (СС, 1923 г.).

Начало исследований положено по монаршей воле: для пополнения государственной казны прусский король Фридрих II решил использовать генуэзскую лотерею, а Эйлеру пришлось его консультировать. В результате появилось несколько статей, в которых рассмотрены следующие проблемы:

· Решена задача определения вероятности появления номеров, следующих друг за другом, даже определена цена билета. Например, при вытаскивании 5 билетов из 90, затем задача сформулирована в общем виде.

· В статье «Вычисление вероятности в игре «встреча»» чётко виден метод решения многих последующих задач: сначала рассматриваются простейшие частные случае, а затем решается задача в общем виде.

Правила игры: 2 игрока с полными колодами карт извлекают поочередно карты до появления одинаковой карты, тогда один из них выигрывает, если нет – то выиграл 2-ой. Нужно определить вероятности выигрыша каждого игрока.

Эйлер начинает решать с условия, что каждый имеет по одной карте, тогда, затем по 2, по 3, по 4 и только после этого переходит к общему случаю. В конце статьи следует вывод: если количество карт бесконечно, то вероятность выигрыша 1-го выразилась бы бесконечным рядом, а 2-го - рядом.

· Успехи наук, в основном, физики выдвинули на первое место важность нахождения наиболее вероятных значений. Д. Бернулли (1777 г.) предложил весьма сложный способ оценки максимального правдоподобия, сводящийся к решению уравнения 5 степени с 20 членами. Эйлер в статье «Замечания к предыдущей статье прославленного Бернулли» удачно совместил свой способ со способом Бернулли и получил в качестве уравнения правдоподобия довольно простое уравнений 3 степени, часто сводящееся к квадратному.

· особенно значимы исследования Эйлера по приложению ТВ к демографии, в которых

ü введены основные её понятия (вероятностная продолжительность жизни; прирост населения; порядок вымирания),

ü создана законченная теория повозрастной смертности,

ü рассмотрены вопросы страхования,

ü сделан расчёт пожизненных рент.

Итак, в ТВ Эйлер не рассматривал общие идеи и понятия, решая конкретные, важные для практики задачи.

Литература

1. Демидов, С.С. Возникновение теории дифференциальных уравнений с частными производными // Историко-математические исследования. - М.: Наука, 1975. - № 20. - С. 204-220.

2. Берман, Г.Н. Число и наука о нем. Общедоступные очерки. – М.: ГИТТЛ, 1984.

3. Стиллвелл, Д. Математика и ее история. - Москва-Ижевск: ИКИ, 2004. - 530 с.

4. Юшкевич, А. П. История математики в России. - М.: Наука, 1968.

Дата добавления: 2014-01-03