Примеры обозначений

(a, b)Σ, a ≤ b; (a, b)Î<, a < b.

Если упорядоченная пара (a, b) принадлежит отношению < или £, элементы а и b называются сравнимыми между собой. Множество М, на котором определено отношение частичного порядка, называется частично упорядоченным. Если на множестве М задан линейный порядок, его называют линейно упорядоченным множеством.

По самому определению линейного порядка в линейно упорядоченном множестве любые два различных элемента сравнимы между собой.

Пример 1. Рассмотрим множества R, Q, Z, N. Отношение сравнения < на этих множествах определяет линейный строгий порядок с точки зрения обычного сравнения чисел.

Например, (2, 5)Î <, (3, 3)Ï <.

Пример 2. Отношение сравнения £ на множествах R, Q, Z, N определяет линейный нестрогий порядок, с точки зрения обычного сравнения чисел, (2, 5)Î £, (3, 3)Î £.

Пример 3. Отношение включения Í определяет нестрогий частичный порядок на булеане 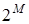, так как не всякие два множества можно сравнить с точки зрения отношения включения.

Пример 4. На множестве натуральных чисел N введем следующее отношение порядка: m £ n Û m делит n. Это – нестрогий частичный порядок: 1 £ 7,

4 £ 12, 6 £ 6, 2 £ 6, (2, 7)Ï £, (9, 12)Ï £.

Конечные частично упорядоченные множества можно изобразить диаграммой, которая называется диаграммой Хассе. Она состоит из кружков (элементов) и линий со стрелками. Если a < b (a £ b), то от элемента a выходит линия со стрелкой, входящая в элемент b. При этом элемент a размещается на диаграмме ниже элемента b.

Пример 5. A = {2, 3, 4, 6, 8, 9}, a £ b Û a делит b. Диаграмма Хассе показана на рис. 1. В силу транзитивности отношения порядка не нужно, например, соединять линией элементы 2 и 8: 2 £ 4, 4 £ 8 Þ 2 £ 8.

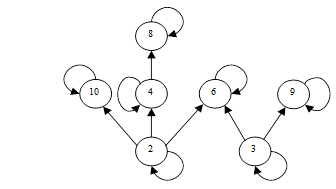
Рис. 1

Так как был определен нестрогий порядок (2 делит 2 Þ 2£2; 3 делит 3 Þ 3£3 и т.д.), то стрелки замыкаются на кружках, образуя петли.

Если определить строгий порядок, a < b Û a делит b и a ≠ b,то петли исчезнут.

Пример 5. Выписать явно бинарное отношение строгого частичного порядка, соответствующее диаграмме Хассе (рис. 2). Указать все элементы, не сравнимые с элементом а и не сравнимые с элементом d.

Дата добавления: 2014-01-03