Свойства математического ожидания

1. Математическое ожидание постоянной равно самой постоянной:

М (С) = С. (2)

Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С) = С ·1 = С.

2. Постоянный множитель можно выносит за знак математического ожидания:

М (СХ) = С М (Х). (3)

Доказательство. Если случайная величина Х задана рядом распределения

xi	x1	x2	…	xn
pi	p1	p2	…	pn

то ряд распределения для СХ имеет вид:

Cxi	Cx1	Cx2	…	Cxn
pi	p1	p2	…	pn

Тогда М (СХ) = Сх ₁ р ₁ + Сх ₂ р ₂ + … + Сх_пр_п = С (х ₁ р ₁ + х ₂ р ₂ + … + х_пр_п) = СМ (Х).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:

M (XY) = M (X) · M (Y). (4)

Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:

xi	x 1	x 2
pi	p 1	p 2

уi	у 1	у 2
gi	g 1	g 2

Тогда ряд распределения для XY выглядит так:

ХY	x 1 y 1	x 2 y 1	x 1 y 2	x 2 y 2
p	p 1 g 1	p 2 g 1	p 1 g 2	p 2 g 2

Следовательно,

M (XY) = x ₁ y ₁· p ₁ g ₁ + x ₂ y ₁· p ₂ g ₁ + x ₁ y ₂· p ₁ g ₂ + x ₂ y ₂· p ₂ g ₂ = y ₁ g ₁(x ₁ p ₁ + x ₂ p ₂) +

+ y ₂ g ₂(x ₁ p ₁ + x ₂ p ₂) = (y ₁ g ₁ + y ₂ g ₂)(x ₁ p ₁ + x ₂ p ₂) = M (X)· M (Y).

Замечание 4. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.

Замечание 5. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции.

Определение 2. Определим сумму случайных величин Х и Y как случайную величину Х + Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго).

4. Математическое ожидание суммы двух случайных величин (зависимых или независимых) равно сумме математических ожиданий слагаемых:

M (X + Y) = M (X) + M (Y). (5)

Доказательство. Вновь рассмотрим случайные величины, заданные рядами распределения, приведенными при доказательстве свойства 3. Тогда возможными значениями X + Y являются х ₁ + у ₁, х ₁ + у ₂, х ₂ + у ₁, х ₂ + у ₂. Обозначим их вероятности соответственно как р ₁₁, р ₁₂, р ₂₁ и р ₂₂.

Найдем

М (Х + Y) = (x ₁ + y ₁) p ₁₁ + (x ₁ + y ₂) p ₁₂ + (x ₂ + y ₁) p ₂₁ + (x ₂ + y ₂) p ₂₂ =

= x ₁(p ₁₁ + p ₁₂) + x ₂(p ₂₁ + p ₂₂) + y ₁(p ₁₁ + p ₂₁) + y ₂(p ₁₂ + p ₂₂).

Докажем, что р ₁₁ + р ₂₂ = р ₁. Действительно, событие, состоящее в том, что X + Y примет значения х ₁ + у ₁ или х ₁ + у ₂ и вероятность которого равна р ₁₁ + р ₂₂, совпадает с событием, заключающемся в том, что Х = х ₁ (его вероятность – р ₁). Аналогично доказывается, что p ₂₁ + p ₂₂ = р ₂, p ₁₁ + p ₂₁ = g ₁, p ₁₂ + p ₂₂ = g ₂.

Значит,

M (X + Y) = x ₁ p ₁ + x ₂ p ₂ + y ₁ g ₁ + y ₂ g ₂ = M (X) + M (Y).

Замечание 6. Из свойства 4 следует, что математическое ожидание суммы любого числа случайных величин равна сумме математических ожиданий слагаемых.

Если 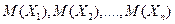существуют, то

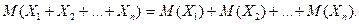
Доказательство. Применяя свойство 4 и метод математической индукции, получим

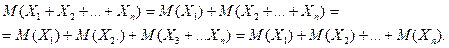
Замечание 7. Свойства 2) и 4) называются свойствами линейности математического ожидания. Обратим внимание на то, что линейность имеет место всегда, без каких-либо дополнительных предположений, кроме предположения о существовании самих математических ожиданий.

5). Есл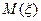и и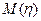существуют и 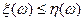для всех 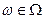, то≤ .

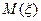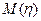Доказательство. Так как при каждом 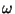имеет мес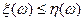то , то

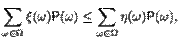
что влечет ≤ .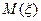

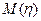В частности, если 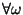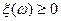, то математическое ожидание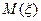неотрицательно при условии, что оно существует.

Задача 3. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей.

Решение. Найдем математическое ожидание числа очков, выпавших при броске одной кости:

М (Х ₁) =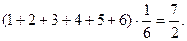

Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4

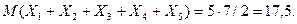
Дата добавления: 2014-01-03