Ядро функции (Kerf)

Пусть f: X ® Y – функция. Ядро функции f определяется обычным образом, Kerf = f 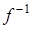Í X ´ X.

Опишем свойства бинарного отношения Ker f, когда f - функция. Найдем сначала ядро биекции.

Если y= f (x) – биекция, то x= 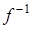(y) определяется однозначно. Имеем

f 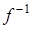(x) = 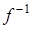(f (x)) = 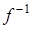(y) = x Þ f = .

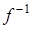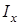Соответственно f 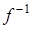(у) = 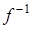(f (у)) = 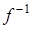(х) = у Þ f 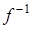=I_у.

Таким образом, ядро биективной функции – это тождественное отображение области определения функции на нее же.

В общем случае 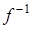уже не функция, а просто бинарное отношение, и тогда справедливо такое утверждение.

Утверждение.

Ядро функции – это отношение эквивалентности на области определения функции.

Доказательство. Выясним, какие упорядоченные пары принадлежат ядру функции f.

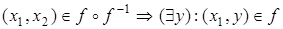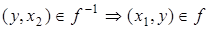и и 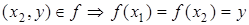. Если пара (x ₁, x ₂) принадлежит ядру, то у элементов этой пары один и тот же образ.

f (x ₁) = f (x ₂) = y Þ (x ₁, y)Î f и (x ₂, y)Î f Þ(x ₁, y)Î f и (y, x ₂)Î 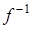Þ (x ₁, x ₂)Î f .

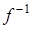Таким образом, (x ₁, x ₂)Î f 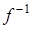Û f (x ₁) = f (x ₂).

Теперь нетрудно доказать, что f 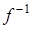– рефлексивное, симметричное и транзитивное бинарное отношение.

1. Рефлексивность: f (x) = f (x) Þ (x, x)Î Kerf;

2. Симметричность: Если f (x ₁) = f (x ₂), то f (x ₂) = f (x ₁). Значит, (x ₁, x ₂)Î Kerf Þ (x ₂, x ₁)Î Kerf;

3. Транзитивность: Если f (x ₁) = f (x ₂), f (x ₂) = f (x ₃), то f (x ₁) = f (x ₃); (x ₁ ,x ₂)Î Kerf и (x ₂, x₃)Î Kerf Þ (x ₁, x ₃)Î Kerf.

Как было показано, всякое отношение эквивалентности определяет разбиение множества, на котором оно задано, на непересекающиеся непустые классы эквивалентности. В случае ядра функции, класс эквивалентности состоит из всех элементов области определения, имеющих один и тот же образ.

Пример.

Возьмем y = sin(x). Тогда [0]={ kp, k Î Z},

[p/6]={π/6 + 2 k π, k Î Z} 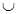{5/6π+2 k π, k Î Z};

[-p/2]={-π/2 + 2 k π, k Î Z} и т.д.

В заключение приведем ещё несколько примеров решения задач.

Пример 1. Пусть Х, Y – два множества, состоящие из n и m элементов соответственно. Какова мощность множества всех тотальных функций, определенных на Х, со значениями в Y?

Решение. Чтобы задать любую тотальную функцию нужно выполнить одно за другим и независимо одно от другого n действий: указать образ каждого элемента множества Х. Но каждое действие можно выполнить m способами Þ число функций равно mⁿ.

Пример 2. Доказать, что 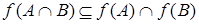, где f – произвольная функция, и что равенство получается, когда 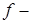инъекция. Привести пример строгого включения.

Решение.

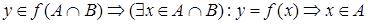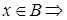
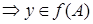1. и

и .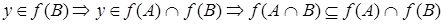

2. Если 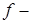инъекция, условие однозначности выполнено также и для значений функции 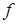, по каждому значению 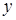однозначно определяется аргумент 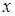, значение которого равно .

,

, .

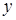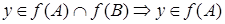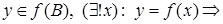
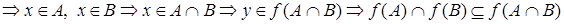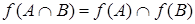3. Если 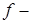не инъекция, то множества 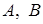аргументов могут вообще не пересекаться, а множества 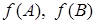значений могут иметь не пустое пересечение. Положим 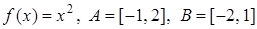. Тогда , , ,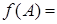

.

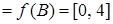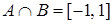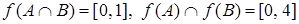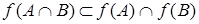Пример 3. Доказать, что .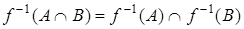

Решение.

,

, .

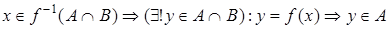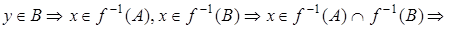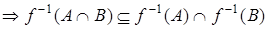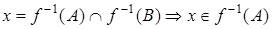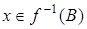, и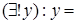

.

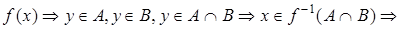
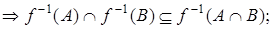
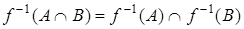Замечание. Запись 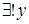читается так: существует и единственен элемент .

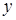Дата добавления: 2014-01-03