Направление вогнутости кривой

Лекция № 9

Тема: «Общее исследование функции»

Изучим свойства графика, связанные с понятием выпуклости и вогнутости.

0.1.1. График дифференцируемой функции 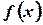называется выпуклым на 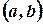, если он расположен ниже любой своей касательной на этом интервале.

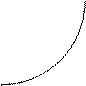
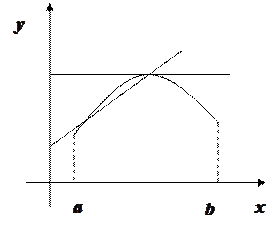
0.1.2. График дифференцируемой функции называется вогнутым на 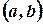, если он расположен выше любой своей касательной на этом интервале.

График функции в одних интервалах может быть вогнутым, а в других выпуклым.

Рассмотрим достаточный признак, позволяющий установить, является ли график функции в данном интервале выпуклым или вогнутым.

Т.1.1 (достаточное условие выпуклости или вогнутости)

Пусть функция 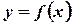имеет вторую производную во всех точках интервала 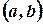. Если во всех точках этого интервала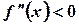, то график функции в этом интервале – выпуклый, если же 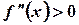- вогнутый.

Доказательство.

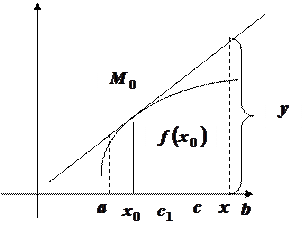Допустим, что 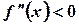- покажем, что график выпуклый.

Установим, что график функции в интервале ниже касательной, т.е. покажем, что для одной и той же абсциссы ордината кривой меньше касательной.

Уравнение графика 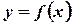, а уравнение касательной в точке 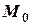имеет вид

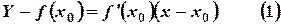
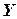- ордината касательной, соответствующая абсциссе .

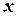Разность ординат графика функции и касательной

или

Преобразуем 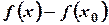по формуле Лагранжа.

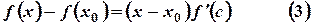
где .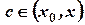

Тогда

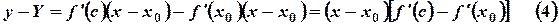
Разность 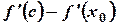снова преобразуем по формуле Лагранжа.

,

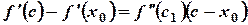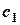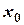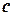где заключена между и и .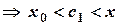

Подставив в равенство (4) получим

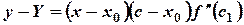
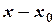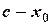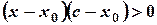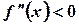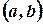Разности и имеют одинаковые знаки, следовательно . Т.к. в , то 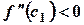. Поэтому

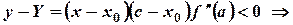ордината касательной больше ординаты графика, т.е. график функции выпуклый.

О.1.3 Точка 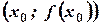графика функции, отделяющая его выпуклую часть от выгнутой или наоборот, называется точкой перегиба.

Т.1.2 (необходимое условие наличия точки перегиба)

Пусть функция 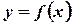имеет в интервале непрерывную . Тогда, если точка с абсциссой 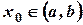является точкой перегиба графика данной функции, то .

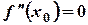О.1.4 Точка в которой 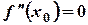или не существует называется подозрительной на перегибе.

Т.1.3 (достаточное условие существования перегиба)

Если вторая производная непрерывной функции меняет знак при переходе через 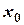, то точка с абсциссой 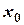- является точкой перегиба функции.

Дата добавления: 2014-01-03