Метод сопряженных градиентов

Вернемся к минимизации квадратичной формы, заданной в виде (24). При ее минимизации методом наискорейшего спуска требовалось, вообще говоря, бесконечно много итераций. Однако существуют такие направления спуска, при которых квадратичная форма (24) с положительно определенной и симметричной матрицей A может быть минимизирована точно за конечное число шагов.

Положительно определенная матрица позволяет ввести норму вектора x по формуле:

|| x ||² = (x, Ax) > 0, когда x ¹ 0, (34)

при этом можно проверить, что все аксиомы нормы выполнены.

Согласно определению нормы в (34), можно ввести скалярное произведение пары векторов x и y по формуле: (x, Ay). Векторы ортогональные в смысле данного скалярного произведения при (x, Ay) = 0 называются сопряженными по отношению к данной матрице A. Оказывается, что поочередный спуск по сопряженным направлениям особенно выгоден при минимизации квадратичной формы.

На идее спуска по сопряженным направлениям базируется множество методов: сопряженных градиентов, сопряженных направлений, параллельных касательных и некоторые другие. Все эти методы одинаково хорошо применимы при минимизации квадратичной формы. Метод сопряженных градиентов может быть легко обобщен на произвольные функции.

Пусть матрица A квадратичной формы имеет размер n ´ n и пусть определены n попарно сопряженные вектора x ₁,…, x_n, т.е. такие вектора, что

(x_i, Ax_j) = d_ij. (35)

Легко доказать от противного, что система векторов x ₁,…, x_n является линейно независимой системой. Выберем некоторую произвольную точку r ₀, тогда произвольное движение из этой точки можно разложить по сопряженному базису, т.е.

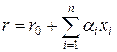. (36)

Подставляя (36) в квадратичную форму (24) и после учета (35), находим

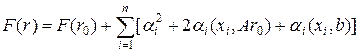. (37)

Из вида квадратичной формы следует, что движение по одному из сопряженных направлений не затрагивает другие направления при минимизации квадратичной формы. Таким образом, если последовательно спускаться по сопряженным направлениям, то минимум можно найти точно за n шагов, равному числу сопряженных направлений. Реально не всегда удается уложиться в n шагов, поскольку порождение ортогонального базиса сопряженных направлений сопровождается значительной потерей точности.

Приведем алгоритм спуска с помощью метода сопряженных градиентов. В качестве первого вектора из набора сопряженных векторов выберем произвольный вектор x ₁. В качестве первого направления движения от вектора x ₁ выберем направление антиградиента в этой точке, т.е. P ₁ = -2 Ax ₁ - b. Первый шаг процесса выглядит следующим образом: .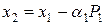

Пусть теперь сделан k -й шаг, т.е. верно равенство

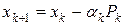. (38)

Для определения неизвестного параметра a_k подставим (38) в квадратичную форму (24) и найдем минимум функции 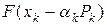от a_k. Это легко сделать, т.к. зависимость от a_k квадратичная, т.е.

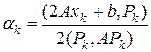. (39)

Подставляя (39) в (38), найдем точку 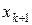начала спуска на следующем шаге. Направление спуска на следующем шаге будем искать, исходя из формулы:

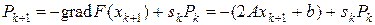, (40)

где s_k — неопределенный коэффициент, который найдем из условия того, что направления P_k и P_{k +1} являются сопряженными. Умножим уравнение (40) на матрицу A слева, а затем скалярно на P_k, тогда, учитывая условие сопряжения 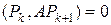, находим

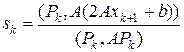. (41)

Формулы (38) — (41), включая первый шаг, полностью определяют алгоритм метода сопряженных градиентов на примере минимизации квадратичной формы (24).

На листинге_№8 приведен код программы поиска минимума квадратичной формы (24) методом сопряженных градиентов на основе алгоритма (38) — (41).

Листинг_№8

%Программа поиска минимума квадратичной формы

%F(r)=(r,Ar)+(b,r)+c методом сопряженных градиентов

%очищаем рабочее пространство

clear all

%определяем размерность квадратичной формы

n=300;

rnd=randn(n);

%определяем параметры квадратичной формы (A=A'>0)

A=rnd'*rnd; b=randn(n,1); c=randn;

%выбираем первый сопряженный вектор и

%соответствующее направление

x(:,1)=randn(n,1);

P(:,1)=-2*A*x(:,1)-b;

%определяем максимальное число шагов метода

%сопряженных градиентов

km=2*n;

%организуем цикл шагов спуска в

%сопряженных направлениях

for k=1:(km-1)

alpha=0.5*((2*P(:,k)'*A*x(:,k)+P(:,k)'*b)/...

(P(:,k)'*A*P(:,k)));

x(:,k+1)=x(:,k)-alpha*P(:,k);

s=(P(:,k)'*(2*A^2*x(:,k+1)+A*b))/...

(P(:,k)'*A*P(:,k));

P(:,k+1)=-2*A*x(:,k+1)-b+s*P(:,k);

%определяем ошибку или погрешность сходимости

%к минимуму квадратичной формы

error(k)=norm(2*A*x(:,k)+b);

end

error(km)=norm(2*A*x(:,km)+b);

%рисуем график зависимости ошибки сходимости к

%минимуму от шага метода сопряженных градиентов

plot(1:km,error);

На рис.11 приведен итог работы программы листинга_№8 в виде зависимости ошибки сходимости к минимуму функции от номера спуска. Ошибка вычислялась как норма градиента функции, т.е. error = ||grad F ||. Рис.11 демонстрирует высокую эффективность минимизации: для размерности квадратичной формы 300 потребовалось приблизительно в два раза больше шагов для точности порядка 10 десятичных знаков.

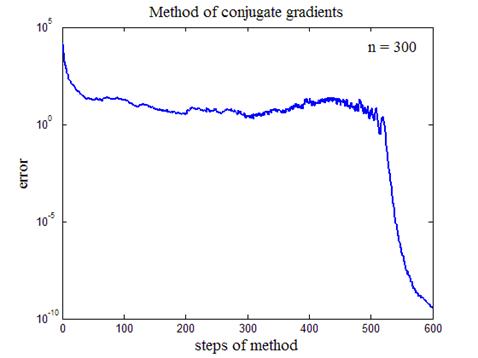
Рис.11. График зависимости ошибки сходимости к минимуму функции
от номера спуска в методе сопряженных градиентов

© Квадратичная форма положительно определена, когда при любых x_i, не равных нулю одновременно, она положительна.

Дата добавления: 2014-01-03