
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема о возрастании (убывании) функции на интервале
|
|
|
|
Необходимое условие возрастания (убывания) функции на интервале: Если функция 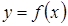 , имеющая производную на отрезке
, имеющая производную на отрезке 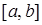 , возрастает (убывает) на этом отрезке, то ее производная
, возрастает (убывает) на этом отрезке, то ее производная 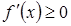 (
(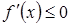 ) на этом отрезке.
) на этом отрезке.
Достаточное условие возрастания (убывания) функции на интервале: Если функция 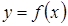 непрерывна на отрезке
непрерывна на отрезке 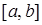 и дифференцируема на интервале
и дифференцируема на интервале 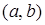 , причем
, причем 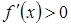 (
(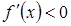 ) для
) для 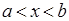 , то эта функция возрастает (убывает) на этом отрезке.
, то эта функция возрастает (убывает) на этом отрезке.
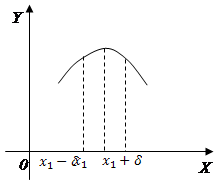 Доказательство легко получается применением теоремы Лагранжа.
Доказательство легко получается применением теоремы Лагранжа.
Определение 1. Функция 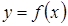 в точке
в точке 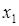 имеет максимум, если для всех x из некоторой
имеет максимум, если для всех x из некоторой 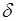 -окрестности точки
-окрестности точки 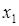 выполняется неравенство
выполняется неравенство 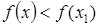 при
при 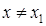 .
.
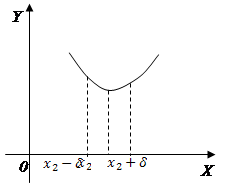 Определение 2. Функция
Определение 2. Функция 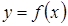 в точке
в точке 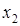 имеет минимум, если для всех x из некоторой
имеет минимум, если для всех x из некоторой 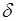 -окрестности точки
-окрестности точки 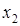 выполняется неравенство
выполняется неравенство 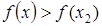 при
при 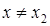 .
.
Определение 3. Точки максимума и минимума функции называются точками экстремума.
Теорема о необходимом условии экстремума дифференцируемой функции. Необходимым условием экстремума дифференцируемой в точке 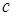 функции является
функции является 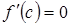 .
.
 Доказательство. Пусть точка
Доказательство. Пусть точка 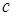 - точка максимума, тогда при подходе к этой точке слева она возрастает и
- точка максимума, тогда при подходе к этой точке слева она возрастает и 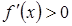 , после прохождения этой точки функция убывает и
, после прохождения этой точки функция убывает и 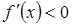 , следовательно, производная существует в точке
, следовательно, производная существует в точке 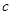 и меняет знак при переходе через нее. Ясно, что
и меняет знак при переходе через нее. Ясно, что 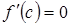 .
.
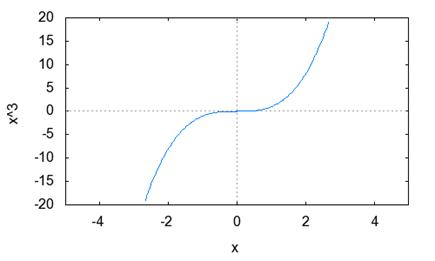
Но необходимое условие не является достаточным условием экстремума. Например, если 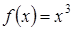 , то
, то 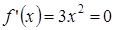 при
при  , но точка
, но точка  не является точкой экстремума.
не является точкой экстремума.
Теорема 1 о достаточном условии существования максимума и минимума функции.
 Если производная функции при переходе через точку
Если производная функции при переходе через точку  меняет знак с + на –, это точка максимума. Если знак производной меняется с – на +, имеем точку минимума. Доказательство следует из теоремы о возрастании (убывании) функции.
меняет знак с + на –, это точка максимума. Если знак производной меняется с – на +, имеем точку минимума. Доказательство следует из теоремы о возрастании (убывании) функции.
Теорема 2 о достаточном условии существования максимума и минимума функции. Пусть 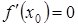 , тогда при
, тогда при 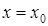 функция имеет максимум, если
функция имеет максимум, если 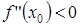 и минимум, если
и минимум, если 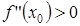 .
.
|
|
|
Доказательство.
Из формулы Тейлора в окрестности точки экстремума 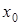 , в которой удержано три первых члена, имеем
, в которой удержано три первых члена, имеем
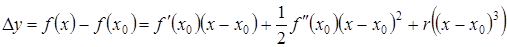 .
.
Поскольку 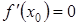 , что следует из условия теоремы, а остаточный член
, что следует из условия теоремы, а остаточный член 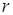 по определению меньше предыдущего члена формулы, знак приращения функции независимо от того, точка
по определению меньше предыдущего члена формулы, знак приращения функции независимо от того, точка 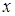 находится левее, или правее
находится левее, или правее 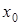 , определяется знаком второй производной. Когда
, определяется знаком второй производной. Когда 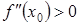 , получаем
, получаем 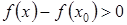 , следовательно,
, следовательно, 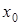 - точка минимума функции, если
- точка минимума функции, если 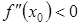 , значит
, значит 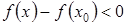 , тогда
, тогда 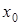 - точка максимума функции.
- точка максимума функции.
Пример. 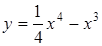 .
. 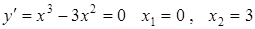 .
.
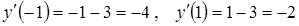 . В точке 0 экстремума нет.
. В точке 0 экстремума нет.
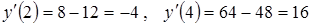 . В точке 3 минимум функции.
. В точке 3 минимум функции.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1218; Нарушение авторских прав?; Мы поможем в написании вашей работы!