Обоснование алгоритма

Пусть мы находимся в некоторой вершине 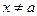. В исходном графе 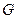степень вершины 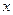— четное число, поэтому после зачеркивания ребер, по которым мы приходили и уходили из вершины 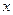, ее степень — нечетна. Следовательно, существует, по крайней мере, одно незачеркнутое ребро, инцидентное вершине 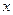. Если это ребро — единственное, инцидентное вершине 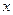, то оно, в силу замечания в 5° алгоритма, не может быть «перешейком», и по нему можно покинуть вершину .

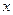Пусть ребер, инцидентных вершине 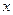— нечетное число, большее единицы. Докажем, что среди них хотя бы одно ребро не является перешейком. Допустим противное: все ребра, инцидентные вершине 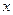— перешейки. Удалим одно из этих ребер, такое, чтобы вершина 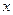и 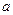оказались в разных компонентах связности. Такое ребро существует, так как в противном случае вершины 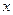и 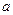были бы связаны более чем одной простой цепью. Это означало бы, что существует простой цикл, содержащий вершины 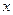и 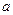. Но ребра, входящие в простой цикл, не могут быть перешейками.

Рассмотрим компоненту связности 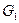, содержащую вершину 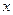(и не содержащую вершину 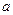). В графе 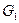степени всех вершин, в том числе и вершины 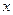— четные числа. Следовательно, в графе существует эйлеров цикл. Ребра, входящие в цикл, не могут быть перешейками.

Итак, наше допущение ведет к противоречию. Более того, мы убедились, что среди ребер, инцидентных вершине 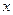в графе, полученном из графа 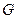удалением пройденных ребер, лишь одно может быть перешейком.

Таким образом, доказано, что невозможность выполнить предписания алгоритма может возникнуть только в вершине 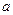, если попасть в нее, по крайней мере, во второй раз. В отличие от других вершин степень вершины 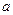при 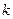-м попадании в нее 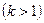— четна. Если эта степень равна нулю, алгоритм перестает работать.

Докажем, что в этом случае эйлеров цикл уже построен. В самом деле, в силу правила 3° любое ребро может войти в цикл 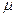не более одного раза. В силу правил 4°, 5° — пройдены все ребра. Действительно, непройденные ребра определяют в графе компоненты связности. Если эти компоненты можно связать с вершиной 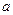цепью из более чем одного зачеркнутого ребра, то среди этих ребер наверняка одно — перешеек; если одним ребром, то была возможность выбора ребра, не ведущего в вершину .

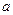Дата добавления: 2014-01-03