Обыкновенная и скомпенсированная кривые спроса

И косвенной функции полезности.

Взаимосвязь функций полезности, потребительских расходов

Обычная функция полезности U (Q_x, Q_y), определенная на потребительском множестве товаров X и Y, напрямую представляет предпочтения потребителя в отношении этих двух товаров, показывая уменьшение потребляемого количества одного товара при увеличении потребления другого (карта безразличия). Поэтому она называется прямой функцией полезности. При заданных ценах и доходе потребитель выбирает набор E (Q_x^*; Q_y^*), максимизирующий его полезность. Уровень полезности, достигаемый при выборе данного набора, будет наивысшим из всех, которые допускаются бюджетным ограничением потребителя при заданных ценах и доходе. Различные цены или доход будут задавать различные бюджетные ограничения, что в общем случае повлияет на выбор потребителя и итоговый уровень полезности.

Соотношение между ценами, доходом и значением полезности можно определить с помощью функции U = ν(P_x, P_y, I), которая называется косвенной функцией полезности. Это функция максимальных значений, соответствующая задаче максимизации полезности потребителя. Если функция U (Q_x, Q_y) непрерывна, то ν(P_x, P_y, I) корректно определена для всех положительных значений цен и дохода. Если, кроме того, U (Q_x, Q_y) квазивогнута (при этом кривые безразличия имеют классическую форму), то оптимальный выбор единственен и соответствует функции спроса потребителя. Другими словами, максимально возможный уровень полезности будет достигаться тогда, когда выбирается набор с количеством товаров, соответствующим функции спроса потребителя.

ν(P_x, P_y, I) = max U (Q_x, Q_y), где Q_x = f (P_x, P_y, I) и Q_y = f (P_x, P_y, I).

ν(P_x, P_y, I) = U (Q_x^*, Q_y^*), где (Q_x^*; Q_y^*) – оптимальный потребительский выбор.

Геометрически можно представить, что ν(P_x, P_y, I) задает уровень полезности, соответствующий самой высокой кривой безразличия, достижимой потребителем при заданных ценах и доходе (рис. 1.10). Если прямая функция полезности непрерывна и возрастает, то косвенная функция полезности обладает следующими свойствами:

1) ν(P_x, P_y, I) непрерывна;

2) однородна нулевой степени по ценам и доходу;

3) возрастает при увеличении дохода;

4) не возрастает при увеличении цен;

5) квазивыпукла по ценам и доходу;

6) если ν(P_x, P_y, I) дифференцируема и ее первая производная по доходу не равна нулю, то оптимальные количества товаров можно найти как

,

.

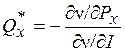Чтобы построить косвенную функцию полезности, мы фиксировали рыночные цены товаров и доход потребителя и искали максимальный достижимый уровень полезности.

Не менее интересен вопрос, какой минимальный объем денежных расходов потребитель должен понести при данных ценах, чтобы достичь заданного уровня полезности? Ответ на этот вопрос дает функция расходов. Для ее построения мы снова фиксируем цены, но абстрагируемся от любых ограничений, связанных с доходом потребителя (просто спрашиваем, сколько потребителю придется потратить, чтобы получить некоторый уровень полезности).

Каждая из бюджетных линий на рис. 1.11 изображает все товарные наборы, для приобретения которых требуется один и тот же объем совокупных расходов при заданных ценах P_x и P_y. Каждая из этих прямых задается уравнением C = P_xQ_x + P_yQ_y для различных объемов совокупных расходов C. Чем дальше бюджетная линия (она же прямая совокупных расходов) от начала координат, тем более дорогие товарные наборы она содержит. Оптимальным будет уровень расходов С^*, который является минимально необходимым и достаточным для получения заданной полезности U.

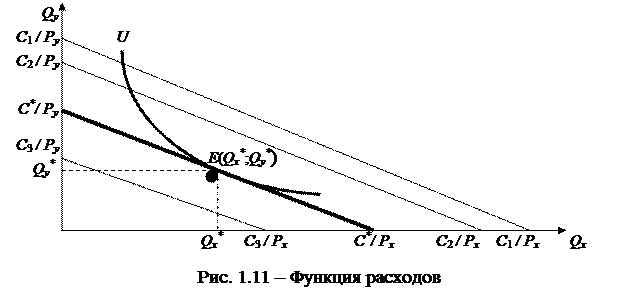
Соответственно, самым дешевым товарным набором, приносящим заданную полезность, будет набор E (Q_x^*; Q_y^*). Минимальный объем расходов равен стоимости этого набора C^* = P_xQ_x^* + P_yQ_y^*.

В общем виде функция расходов определяется как функция минимальных значений

C (P_x, P_y, U) = min (P_xQ_x + P_yQ_y), для всех неотрицательных цен и всех достижимых уровней полезности U (Q_x, Q_y).

Таким образом, мы видим, насколько тесно задача максимизации полезности потребителя связана с его наблюдаемым спросом на рынке. Решение же задачи минимизации расходов E (Q_x^*; Q_y^*) можно интерпретировать как другой вид «функции спроса» – но такой, которая не наблюдаема напрямую.

Свойства функции расходов:

1) наименьшее ее значение равно нулю;

2) функция непрерывна;

3) для всех неотрицательных цен функция расходов возрастает при росте цен и неограниченна сверху по полезности;

4) функция расходов не убывает по ценам;

5) однородна первой степени по ценам;

6) вогнута по ценам;

7) функция расходов дифференцируема по ценам, причем оптимальный товарный набор может быть определен как

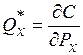и .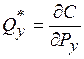

Представим себе гипотетическую ситуацию, когда любое изменение полезности, происходящее вследствие повышения или понижения цен, компенсируется изменением полезности за счет снижения или роста дохода. В таком случае мы получим гипотетические функции спроса с постоянной полезностью, при построении которых игнорируется тот уровень полезности, которого действительно может достичь потребитель. Такие функции называются функциями компенсированного спроса или хиксовскими [1] функциями спроса (рис. 1.12).

Рассмотрим рис. 1.12. Если мы хотим зафиксировать достижимую потребителем полезность на уровне U и задать цены P_{x 1}, P_{y 1}, то его бюджетное ограничение будет иметь наклон – P_{x 1} / P_{y 1}. Заметим, что максимизация полезности и минимизация расходов происходят в одной и той же точке с координатами (Q_{x 1}; Q_{y 1}). Если снизить цену товара X до P_{x 2}, оставляя потребителя на той же кривой безразличия с уровнем полезности U, путем соответствующего снижения дохода, то новая бюджетная линия будет иметь наклон – P_{x 2} / P_{y 1}, а точка, максимизирующая полезность, получит координаты (Q_{x 2}; Q_{y 1}). Изобразив на графике то гипотетическое изменение количества товара X, которое потребитель «приобретет» в результате снижения цены, если его полезность ограничена уровнем U, получим псевдо-кривую спроса по Хиксу. Очевидно, что кривые хиксовского спроса будут различаться по форме и положению для разных уровней полезности (т.е. для разных кривых безразличия). Хиксовские функции спроса можно легко получить из функции расходов простым дифференцированием (свойство 7 функции расходов).

Между косвенной функцией полезности и функцией расходов, а так же между функциями спроса по Маршаллу и Хиксу существует тесная связь.

1. Математически косвенная функция полезности ν(P_x, P_y, I) и функция расходов C (P_x, P_y, U) являются соответствующим образом подобранными обратными функциями друг друга (их можно вывести одну из другой), т.к. справедливы утверждения

C (P_x, P_y, ν(P_x, P_y, I)) = I;

ν(P_x, P_y, C (P_x, P_y, U)) = U.

2. Маршалловский спрос при ценах P_x, P_y и доходе I равен хиксовскому спросу при тех же ценах и уровне полезности, достижимом при ценах P_x, P_y и доходе I. В свою очередь, хиксовский спрос при любых ценах P_x, P_y и уровне полезности U совпадает с маршалловским спросом при тех же ценах и объеме дохода, равном расходам, минимально необходимым при этих ценах для достижения уровня полезности U. Другими словами, решение задачи максимизации полезности является одновременно и решением задачи минимизации расходов (рис. 1.13). Точка (P_{x 1}, Q_x^*) лежит на всех трех кривых – 1) кривой хиксовского спроса на товар X при ценах P_x, P_y и полезности U; 2) кривой хиксовского спроса на товар X при ценах P_x, P_y и полезности ν; 3) кривой маршалловского спроса на товар X при ценах P_x, P_y и доходе I.

Отсюда следуют два важных положения, характеризующих проблему оптимизации потребительского спроса:

1) сбалансированность бюджета потребителя, достигаемая при совершении оптимального выбора (расходы равны доходу);

2) возможность не учитывать (полностью исключить из анализа спроса) деньги как единицу измерения, т.к. спрос зависит только от соотношения цен товаров и реального потребительского дохода.

Кроме того, для любой функции цен и полезности, обладающей всеми свойствами функции расходов, существует прямая функция полезности, которая ее порождает. Следовательно, из функции расходов можно вывести не только косвенную, но и прямую функцию полезности.

U (Q_x, Q_y) = min ν(P_x, P_y, C).

Дифференцирование функции U (Q_x, Q_y) по количеству товара дает нам обратную функцию спроса P_x (Q_x, Q_y).

Дата добавления: 2014-01-03