Интерполяционный ряд Котельникова-Шеннона

Спектр дискретизированного сигнала (7.7) представляет собой сумму сдвинутых копий исходного аналогового сигнала с шагом сдвига, равным частоте дискретизации. Очевидно, что если спектры копий не перекрываются, то по центральной копии дискретного спектра можно восстановить исходный аналоговый сигнал с абсолютной точностью. Умножая функцию (7.6) на прямоугольную весовую функцию П_F(f), равную 1 в пределах главного частотного диапазона [-F/2,F/2] и нулю за его пределами, получаем непрерывный спектр в бесконечных по частоте границах, равный спектру F×S(f) в пределах главного частотного диапазона:

F×S(f) = F×[S(f) _* Ш_F(f)]×П_F(f). (7.9)

Обратное преобразование Фурье такого спектра должно давать конечный и непрерывный сигнал. Произведем обратное преобразование обеих частей равенства (7.9):

F·[S(f) _* Ш_F(f)] Û s_Dt(t), П_F(f) Û F×sinc(pFt).

F×s(t) = s_Dt(t) _* F×sinc(pFt).

s(t) = sinc(pFt) 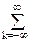_*s(kDt)d(t-kDt),

Дискретизированный сигнал s_Dt(t) =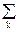s(kDt)d(t-kDt) представляет собой сумму последовательных весовых импульсов Кронекера, сдвинутых на интервал Dt, со значениями веса, равными значениям отсчетов функции s(t) в моменты kDt. При прохождении такого сигнала через систему с импульсным откликом h(t)= sinc(pFt)= sin(pFt)/pFt каждый весовой импульс Кронекера возбудит на выходе соответствующую последовательную серию сдвинутых и масштабированных копий оператора фильтра. Отсюда, с учетом очевидного равенства

d(t-kDt) _* sinc(pFt) = sinc[pF(t-kDt)],

выходной сигнал будет представлять собой сумму сдвинутых весовых импульсных откликов системы, где значение веса определяется отсчетами дискретного сигнала:

s(t) =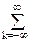s(kDt) sinc[pF(t-kDt)] =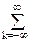s(kDt) sinc[p(t/Dt-k)]. (7.10)

Эта конечная формула носит название интерполяционного ряда Котельникова-Шеннона. Из нее следует, что если наибольшая частота в спектре произвольной непрерывной функции s(t) не превышает частоты ее дискретизации, то она без потери точности может быть представлена в виде числовой последовательности дискретных значений s(kDt), k = 0,1,2,..., и однозначно восстановлена по этой последовательности. В этом и состоит сущность теоремы отсчетов Котельникова. В зарубежной литературе она называется также теоремой Шеннона или теоремой дискретизации (sampling teorem).

По существу, ряд (7.10) представляет собой частный случай разложения сигнала в соответствии с формулой (7.2) по системе ортогональных функций интегрального синуса v(t, kDt)= sinc(pF(t-kDt))= sinc(p(t/Dt – k)), образующих базис пространства сигналов s(t). Для проверки ортогональности достаточно вычислить скалярное произведение базисных функций:

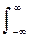v(t,nDt) v(t,mDt) dt = .

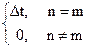Разложение (7.10) проще и понятнее, чем разложение в ряды Фурье, что можно видеть на рис. 7.6. Вес каждой функции отсчетов sinc[pF(t-kDt)] формирует пиковое значение интегрального синуса в каждой текущей точке t= kDt, равное значению сигнала s(kDt), при этом во всех остальных точках дискретных отсчетов sinc[pF(t-(k±j)Dt))], j= 1,2,… значения интегрального синуса равны нулю. Ряд числовых значений интегрального синуса для дискретных значений t= nDt при суммировании по k полностью эквивалентен гребневой функции:

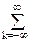sinc[pF(nDt-kDt)] º Ш_Dt(t).

Однако, в отличие от гребневой функции, в интервале между дискретными отсчетами интегральный синус имеет не нулевые, а определенные осциллирующие значения. Суперпозицией этих значений по текущим значениям t от всех интегральных синусов, осцилляции которых доходят до данного значения t, и образуются значения аналогового сигнала в интервалах между отсчетами.

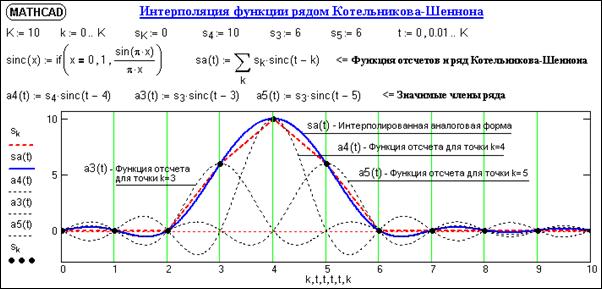
Рис. 7.6. Восстановление непрерывного сигнала по дискретным отсчетам

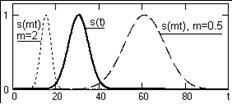
Рис. 7.7	Рис. 7.8 Изменение масштаба при восстановлении аналоговой функции

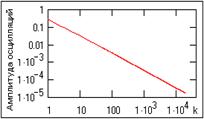
В принципе, функции отсчетов имеют бесконечные осцилляции, и восстанавливают аналоговый сигнал, бесконечный по аргументу. Амплитуда осцилляций функций отсчетов затухает достаточно медленно (см. рис. 7.7). Однако на рис. 7.6 нетрудно заметить, что, в силу знакопеременности функций отсчетов по интервалам дискретизации, осцилляции восстанавливаемых кривых с финитным спектром затухают достаточно быстро, и для данных без существенных выбросов и больших перепадов значений определяются, в основном, отсчетами, ближайшими к интерполируемому интервалу. Это позволяет ограничивать интервал суммирования в формуле (7.8) определенными окрестностями текущих точек интерполяции.

Ряд (7.10) позволяет простым введением масштабного множителя в аргумент интегрального синуса изменять представление сигнала на временной оси, растягивать или сжимать сигнал:

s(t) =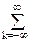s(kDt) × sinc[pF(mt-kDt)].

По аналогичной формуле может выполняться пересчет дискретных данных на другой интервал дискретизации:

s(n·Dt_new) = 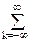s(kDt) × sinc[pF(n·Dt_new-kDt)].

Примеры восстановления аналоговой формы произвольного финитного сигнала и изменения шага дискретизации данных приведены на рис. 7.9.

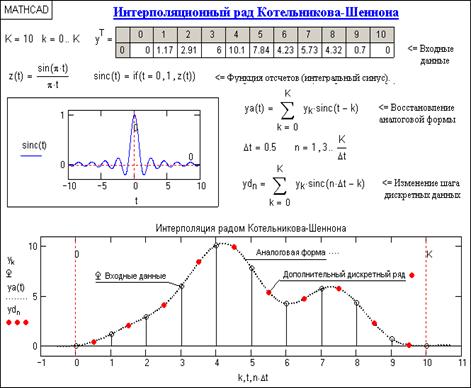
Рис. 7.9. Интерполяция по Котельникову-Шеннону

На рис. 7.10 приведено моделирование дискретизации аналогового сигнала, влияние наложение спектров боковых периодов на спектр главного диапазона дискретного сигнала и восстановление из этого спектра аналоговой формы сигнала.

Графики А и Б рисунка – модельный аналоговый сигнал, точки его дискретизации и модуль спектра дискретного сигнала. Вычисление спектра выполнено быстрым преобразованием Фурье (БПФ) и отображает, соответственно, частотный диапазон 0-2f_N. Дискретизация выполнена корректно, с выполнением условия (7.8), о чем можно судить и по спектру дискретного сигнала (график Б, выход на незначимые значения к частоте Найквиста f_N).

Кривая S1 на графике В – спектр модельного дискретного сигнала при нарушении условия (7.8). В данном случае это произойдет при увеличении шага дискретизации в 2 раза, что вызовет уменьшение в 2 раза новой частоты Найквиста и перемещение границы главного диапазона на отметку 0.5f_N на графике Б, при этом произойдет перекрытие спектров поддиапазонов. На графике приведены кривые S1a и S1b, которые являются раздельными спектрами правой половины главного диапазона без сложения со спектром правого бокового диапазона (интервал 0-2f_N, где f_N – частота Найквиста новой дискретизации), и левой половины правого бокового диапазона на том же интервале 0-2f_N без сложения со спектром главного диапазона. Хорошо видны «хвосты» спектров, выходящие за границы интервала Найквиста от центров диапазонов и заходящие в соседние диапазоны. Сложением этих спектров в интервале 0-2f_N нетрудно убедиться, что полученный результат будет полностью соответствовать спектру S1 новой дискретизации исходного сигнала. Обратим внимание, что сложение спектров рядом расположенных диапазонов может вызывать не только увеличение высокочастотных составляющих (как это можно было видеть на рис. 7.4 – спектр S1), ни и их взаимную компенсацию, как имеет место для спектра S1 в данном случае (кривая точками на графике В).

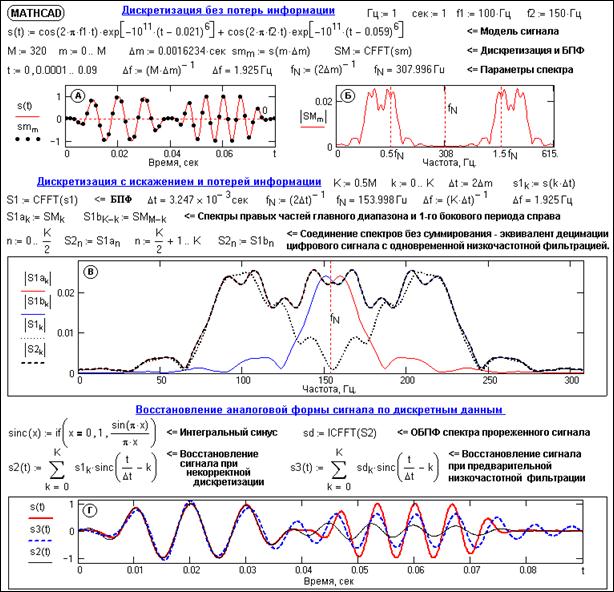
Рис. 7.10. Моделирование дискретизации аналогового сигнала

Перекрытие спектров диапазонов вызовет искажение аналоговой формы сигнала, восстановленного из его дискретных отсчетов, что можно видеть на графике Г – кривая s2. В данном случае, при частичной взаимной компенсации перекрывающихся частей спектров, наиболее сильное искажение произошло во второй, высокочастотной части сигнала.

Дискретизируемые сигналы, как правило, содержат широкополосные шумы, высокочастотные составляющие которых неизбежно перекрываются при периодизации спектра, и увеличивают погрешность восстановления сигналов. Для исключения этого фактора перед проведением дискретизации должно быть обеспечено подавление всех частот выше частоты Найквиста, т.е. выполнена низкочастотная фильтрация сигнала. Если последнее не проведено, то при дискретизации целесообразно в 2-4 раза уменьшить интервал дискретизации относительно оптимального и первой операцией обработки данных выполнить низкочастотную цифровую фильтрацию, после чего можно провести децимацию данных.

Увеличение интервала дискретизации сигналов является довольно распространенной операцией при цифровой обработке данных, и не только при подготовке данных для хранения с целью сокращения их количества. При комплексной обработке данных различной природы интервалы дискретизации этих данных могут оказаться различными, и производится их приведение к одному значению. Аналогичная операция выполняется, как правило, и при создании многослойных информационных пакетов. В таких случаях снижение частоты дискретизации каких-либо данных является вынужденной необходимостью даже с потерей части высокочастотных составляющих информации. Предварительное отфильтровывание отбрасываемых данных перед децимацией (для исключения их попадания в главный частотный диапазон и искажения основной информации) в этом случае является обязательным, особенно при достаточно высокой энергии этих составляющих сигнала. Пример такой децимации приведен на рис. 7.10 на графиках В и Г - спектр S2(f) децимированных данных и аналоговый сигнал s3(t), восстановленный по дискретным отсчетам sd(kDt) ↔ S2(f). Децимация выполнена непосредственно в частотной области путем смыкания на частотной части 0-0.5f_N спектра SM(f) исходного сигнала sm(mDm) с сопряженной частью на интервале 1.5f_N- f_N, что сокращает новый интервал Найквиста в 2 раза и формирует спектр S2(f), соответствующий дискретному сигналу с увеличенным в два раза интервалом дискретизации данных с полностью подавленной частью спектральных составляющих от 0.5f_N до 1.5f_N. Такой метод может применяться для децимации (передискретизации) данных с любой кратностью.

Дата добавления: 2014-01-03