Поэтому для2.6 будет справедлива запись

Симметрийная классификация энергетических уровней

В основе классификации - теория групп. Согласно этой теории уравнение Шредингера для физической системы (атома, иона, молекулы) инвариантно (неизменно) по отношению к операциям симметрии.

При преобразованиях симметрии волновые функции стаци-онарных состояний системы, относящихся к одному и тому же уровню энергии, преобразуются друг через друга, т. е., осущест-вляют некоторое представление группы. Существенно, что это представление неприводимо.

Таким образом, каждому уровню энергии (терму) системы отвечает некоторое неприводимое представление ее группы симметрии. Размерность представления определяет кратность вырождения данного уровня, т. е. число различных состояний с данной энергией.

Симметрия по отношению к изменению знака времени (t ® -t) приводит к тому, что комплексно-сопряженные волновые функции должны относиться к одному и тому же собственному значению энергии.

Если некоторый набор функций и набор комплексно-сопряженных с ними функций осуществляют различные (не эквивалентные) неприводимые представления группы, то эти два комплексно-сопряженных представления должны рассматриваться как одно «физически неприводимое» представление с удвоенной размерностью.

Примером такой группы является группа симметрии C₃, которая имеет только одномерные представления, но два из них комплексно сопряжены и физически соответствуют двукратно-вырожденным уровням энергии.

Вырождение или расщепление энергетических уровней можно проследить на гамильтониане физической системы, которая подвергается воздействию некоторого возмущения определенной симметрии

, (2.4)

Если – гамильтониан нулевого приближения, обладает группой симметрии G_0, – оператор возмущения, обладает группой симметрии G₁., то при совпадении группы симметрии G₁ с группой G₀, снятия возможного вырождения или расщепления вырожденных уровней не произойдет. Можно ожидать лишь смещение энергетического спектра.

Если группа G₁ является подгруппой группы G₀, т. е. симметрия возмущения ниже симметрии невозмущенной системы, то симметрия гамильтониана будет совпадать с симметрией возмущения . Волновые функции, которые осуществляли неприводимое представление группы G₀, будут осуществлять также и представление группы G₁, но оно может оказаться приводимым, что означает расщепление уровня.

Пример 2.8. На примере трехкратно вырожденного уровня энергии, соответствующего неприводимому представлению F₂ группы симметрии T_d() показать действие возмущения симметрии C_3v(G₁), (которая является подгруппой группы симметрии T_d.().

Алгоритм решения: чтобы узнать, как будет влиять возмущающее поле симметрии C_3v на трехкратно вырожденный уровень энергии F₂ группы симметрии Т_d, выписываются характеры неприводимых представлений для общих элементов симметрии группы симметрии C_3v и неприводимого представления F₂ и представляются в виде табл. 2.5.

Табл. 2.5. Характеры неприводимых представлений группы C_3v и уровней энергии F₂ симметрии T_d.

C3v	E	2C3	3sv(ºsd, Td))	ni
A1
A2			-1
E		-1

Проверяется, будет ли представление, характеризуемое характером приводимым в группе симметрии C_3v. Для этого пользуясь формулой

, (2.5.)

где – порядок группы симметрии оператора возмущения симметрии ; h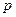- число операций в классе группы симметрии C_3v; 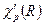– характеры р - го неприводимого представления группы возмущения; – характеры представления уровня энергии F₂ группы симметрии T_d; n – число, показывающее сколько раз p-е неприводимое представление группы симметрии C_3v содержится в представлении F₂.

Результат разложения

; ; .

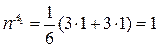сводится в таблицу 2.5.

Таким образом получаем

F₂(T_d) = (A₁+E)(C_3v), (2.6.)

т.е., трехкратно вырожденный уровень F₂ под действием оператора возмущения симметрии C_3v расщепляется на один невырожденный уровень симметрии A₁ и один двукратно вырожденный уровень симметрии Е.

Симметрийный подход используется при анализе функциональных возможностей твердотельных лазерных сред. Лазерные среды представляют собой матрицу основного материала,например, корунд (a = Al₂O₃), флюорит (CaF₂), алюминий-иттриевый гранат (Y₃Al₅O₁₂) с примесями ионов групп железа, редких земель и других.

Примесные ионы, внедренные в решетку кристаллической матрицы, под воздействием внутрикристаллического поля, образуют рабочие уровни квантовой системы.

Теоретико-групповая классификацию уровней энергии активного лазерного материала осуществляется с учетом позиционной симметрии (группа G₁) внедренного иона и его симметрии в свободном состоянии.

Пример 2.8. Проиллюстрировать образование рабочих уровней энергии ионов хрома в кристаллах корунда

Алгоритм решения:_. определяется система уровней энергии свободного иона хрома; полученная система подвергается воздействию сначала внутрикристаллического поля симметрии O_h, характерного для кристаллов , затем воздействию поля тригональной симметрии C_3v, возникающего вследствие неравенства ионных радиусов при замещении ионов алюминия ионами хрома

Основное состояние свободного трехвалентного иона хрома определяется исходя из незаполненной электронной 3d³ оболочки. Согласно правилам Хунда, минимальной энергией будет обладать состояние с наименьшими значениями суммарных квантовых чисел S и L. Таковым будет состояние ⁴F. Этот уровень энергии вырожден семикратно по орбитальному квантовому числу m=2L+1=2×3+1=7 и четырехкратно по спиновому квантовому числу m=2S+1=2×+1=4.

Пользуясь формулой 2.5.

,

получаем, что действие поля кубической и тригональной симметрии приводят к расщеплению ⁴F уровня свободного иона хрома на подуровни, показанные на рис. 2.1.

Рис. 2.1. Расщепление уровней свободного иона хрома под действием полей симметрии O_h и C_3v

В результате 28-кратно вырожденное состояние расщепляется на два орбитальных триплета и один орбитальный синглет.

С точки зрения теории групп действие кристаллического поля привело к расщеплению (2L+1)-кратно вырожденного уровня энергии свободного иона хрома.

Это означает, что представление полной группы вращения, которое осуществляли (2L+1) волновых функций свободного иона хрома оказалось приводимым относительно точечной группы симметрии кристалла.

Таким образом, зная позиционную симметрию внедренного в кристалл иона и симметрию свободного иона можно произвести классификацию термов рассматриваемого материала.

Пример 2.9 Рассмотреть задачу о расщеплении энергетического уровня во внутрикристаллическом поле, исходя из состояния изолированного атома.

Алгоритм решения: анализируется симметрия свободного атома, определяются характеры элементов симметрии для соответствующей группы

Симметрией свободного атома является группа вращений, влияние кристалла на атом рассматривается, как малое возмущение.

Симметрия этого возмущения, т. е. группа G₁, является точечной группой, определяющей кристаллическую сингонию. Схема расщепления энергетических уровней атома получается с помощью формулы 2.5.

Характеры свободного атома с определенным значением орбитального квантового числа (L) для операций вращения, инверсии, отражению в плоскости и зеркального поворота вычисляются по формулам:

(2.7)

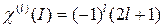. (2.8)

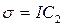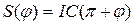; , (2.9)

Процедура симметрийной классификации (энергетических уровней) атомной многоуровневой системы и вычисление правил отбора для переходов представляется в виде следующего алгоритма:

1. Определяется точечная группа симметрии кристалла (G₁).

2. Вычисляются по формулам (2.7 - 2.9).характеры c^(l)(G₁) для заданной электронной оболочки с квантовыми числами (n, l).

3. По формуле 2.5. находится расщепление уровней изолированного атома, внедренного в кристалл симметрии G₁.

4. Определяется позиционная симметрия атома в кристаллической решетке (симметрия возмущения ).

5. Находятся характеры рассматриваемых уровней в группе симметрии возмущения и по формуле (2.5.) определяются изменения в энергетическом спектре.

6. Используя приведенные выше формулы вычисляются правила отбора многоуровневой системы

Пример 2.10: показать расщепление атомного уровняорбитальным квантовым числом l в кристаллическом полеоктаэдра (группа симметрии 0).

Алгоритм решения: с помощью формул (2.7 – 2.9) вычисляем характеры представления группы вращений, соответствующие классам элементов симметрии группы O (табл.2 Приложение 1). Для классов 3C₂, 6, j = p и 6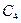, , получим

. (2.10)

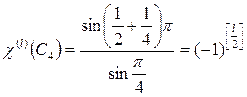, (2.11)

где целая часть l/2.

Классу 8C₃ соответствует ,

т.е., 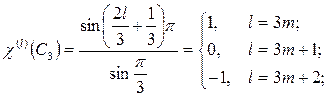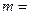0, 1, 2, (2.12)

Для класса Е имеем:

, (2.13)

Результаты вычислений по 2.10 – 2.13 сводятся в табл. 2.6 совместно с характерами группы O.

Табл. 2.6. Расщепление атомных уровней в поле симметрии октаэдра (О)

O	E	3C2	6C4	6C2'	8C3
A1
A2			-1	-1
E					-1
F2		-1	-1
F1; (x, y, z)		-1		-1
c^(^l^): l = 0						A1
l = 1		-1		-1		F1
l = 2			-1		-1	E+F2
l = 3		-1	-1	-1		A2+F1+F2
l = 4						A1+E+F1+F2
l = 5		-1		-1	-1	E+2F1+F2
l = 6						A1+A2+E+F1+2F2

Разлагая характеры c^(l) по формуле (2.5).Например,для L= 3 лучим:

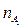= 1/24 [7 × 1 + (-1) × 1 × 3 + (-1) × 1 × 6 + (-1) × 1 × 6 + 1 × 1 × 8] = 0;

= 1/24 [7 × 1 + (-1) × 1 × 3 + (-1) × (-1) × 6 + (-1) × (-1) × 6 + 1 × 1 × 8] = 1;

n_E = 1/24 [7 × 2 + (-1) × 2 × 3 + (-1) × 0 × 6 + (-1) × 0 × 6 + 1 × (-1) × 8] = 0;

= 1/24 [7 × 3 + (-1) × (-1) × 3 + (-1) × 1 × 6 + (-1) × (-1) × 6 + 1 × 0 × 8] = 1;

= 1/24 [7 × 3 + (-1) × (-1) × 3 + (-1) × 1 × 6 + (-1) × 1 × 6 + 1 × 0 × 8] = 1.

Аналогично проводим вычисления для других значений L.

Схема расщепления некоторых уровней свободного атома во внутрикристаллическом поле кубической симметрии представлена на рис. 2.2

Понижение симметрии атома в решетке, например до симметрии C_3v, приводит к дальнейшему снятию вырождения

Рис. 2.2 Схема расщепления уровней энергии свободного атома в поле кубической симметрии.

На рис. 2.3 показано относительное расщепление компонент D-терма в октаэдрическом, тетрагонально искаженном октаэдре и плоско-квадратном комплексах.

Рис. 2.3 Относительное расположение компонент расщепления D-терма в октаэдрическом, тетрагонально искаженном октаэдре и плоскоквадратном комплексе.

Вычисление правил отбора для матричных элементов электрического дипольного момента для системы уравнений симметрии O.

Как видно из табл. 5.3 полярный вектор преобразуется по неприводимому представлению F₁ группы 0, т. е. D_f º F₁.

Прямые произведения F₁ с другими представлениями группы 0, т. е. 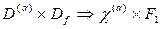, имеют вид:

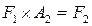; ; ; ; . (2.14)

Справедливость (2.14) можно показать на примере прямого произведения 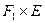. Для этого воспользуемся таблицей характеров представлений и , найдем характеры и занесем их в таблицу

O	E	3C2	6C4	6C2'	8C3
E					-1
F1		-1		-1
F1´E		-2

Учитывая полную таблицу группы симметрии О, разложим F₁´E на неприводимые представления:

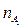= 1/24 [6 × 1 + (-2) × 1 × 3 + 0 × 1 × 6 + 0 × 1 × 6 + 1 × 0 × 8] = 0;

= 1/24 [6 × 1 + (-2) × 1 × 3 + … «0» ] = 0;

n_E = 1/24 [6 × 2 + (-2) × 2 × 3 + … «0» ] = 0;

= 1/24 [6 × 3 + (-2) × (-1) × 3 + … «0» ] = 1;

= 1/24 [6 × 3 + (-2) × (-1) × 3 + … «0» ] = 1.

Таким образом, получим, что F₁´E=. Аналогично можно доказать справедливость остальных соотношений 2.14.

Исходя из того, что произведение D^(a)´D_f содержит D^(b), то пе-реход a ® b возможен (так как матричный элемент не равен ну-лю) и отличными от нуля будут матричные элементы электри-ческого дипольного момента для переходов F₁ «A₁, E, F₁, F₂; F₂ «A₂, E, F₁, F₂.

Симметричные произведения неприводимых представлений группы 0 равны

, , .

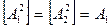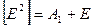Как видно, они не содержат F₁. Поэтому диагональные (по энергии) матричные элементы вектора (инвариантного по отношению к обращению времени) отсутствуют.

2.6 Правила отбора

Знание уровней энергии материала недостаточно для отнесе-ния их к числу возможных для практического применения. Важно, чтобы эти материалы обладали возможностью квантово механических переходов между уровнями энергии.

Такие переходы ограничиваются симметрийными условиями. Учет симметрии позволяет классифицировать термы, дает простой метод нахождения правил отбора для матричных элементов различных величин, характеризующих систему.

Этот метод основан на следующей теореме. Если 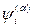– одна из функций базиса неприводимого (неединичного) представления группы симметрии, то ее интеграл по всему конфигурационно-му пространству данной физической системы тождественно обращается в нуль

. (2.15)

Очевидно, что интеграл, взятый по всему пространству, должен быть инвариантен по отношению к любому преобразованию системы координат, в том числе, по отношению к любому преобразованию симметрии.

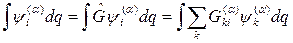. (2.16))

Если это равенство умножить на порядок группы и просуммировать по всем элементам группы, то получим

. (2.17)

Но для всякого неединичного неприводимого представления имеем , следовательно, тождество (5.2) доказано.

Поэтому, если y – функция, относящаяся к базису некоторого, произвольного приводимого представления группы, то интеграл будет отличен от нуля только тогда, когда это представление содержит в себе единичное (в силу 2.16).

Матричные элементы физической величины f имеют вид:

, (2.18)

где индексами a, b отличают различные термы системы, а индексами i, k нумеруют волновые функции, относящиеся к одному и тому же вырожденному уровню.

Обозначим неприводимые представления группы симметрии данной системы, осуществляемые функциям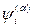и и , символами D^(a) и D^(b)_, а символом D_f - представление той же группы, отвечающее симметрии величины f, имеющей тензорный характер.

Если f – скаляр, то ее оператор f инвариантен по отношению ко всем преобразованиям симметрии, так что D_f – единичное представление.

Если – псевдоскаляр и группа содержит только оси симметрии, то D_f – одномерное, но не единичное представление. Если f – векторная величина, то D_f – представление, осуществляемое тремя компонентами x, y, z. Это представление различно для полярных и аксиальных векторов.

Произведение осуществляет представление группы, выражающееся прямым произведением .

Матричные элементы отличны от нуля, если это представление содержит в себе единичное, или, что то же самое, если прямое произведение 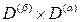содержит в себе D_f. Практически удобнее разлагать на неприводимые части произведение 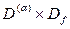, тем самым сразу узнаем все типы D^(b) состояний, для переходов в которые (из состояния типа D^(a)) матричные элементы должны быть отличны от нуля.

Прямым произведением двух представлений является представление, характеры которого определяются как

.

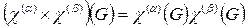Если a = b, то

.(2.19))

Прямое произведение (5.6) можно разбить на два представления меньшей размерности. Первое называется симметричным произведением представления само на себя (характеры обозначаются символом [c²](G)), а второе – антисимметричным произведением (обозначение – {c²}(G)).

, .

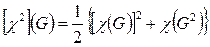Если c^(a)(A) – a-представление группы Â, а c^(b)(B) – b-представление группы 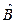, то элементу 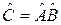группы соответствует характер

,

который является характером неприводимого представления (a´b) группы .

Итак, если D_f – единичное представление (f – скаляр), то отличны от нуля матричные элементы для переходов между состояниями одинакового типа всегда содержит единичное.

Особого рассмотрения требуют диагональные по энергии матричные элементы, т. е. элементы для переходов между состояниями, которые относятся к одному и тому же терму. В этом случае имеем всего одну систему функций 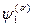, , , 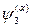…. Правила отбора зависят от поведения величины f при обраще-нии времени t ® -t.

Рассмотрим состояние, описывающееся волновой функцией вида . Среднее значение величины f в этом состоянии дается суммой

.

В состоянии имеем:

. (2.20)

Если величина f инвариантна по отношению к t ® -t, то оба состояния не только относятся к одному и тому же уровню энергии, но должны иметь также и одинаковое значение . Ввиду произвольности коэффициентов C_i это значит, что

.

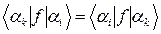Поэтому для нахождения правил отбора надо рассматривать не целиком прямое произведение , а лишь его симметричную часть ; отличные от нуля матричные элементы существуют, если содержит в себе D_f. Если же величина f меняет знак при обращении времени, то замена y ® y^* должна сопровождаться изменением знака . Отсюда тем же способом находим, что

.

В этом случае правила отбора определяются разложением антисимметричной части прямого произведения .

Дата добавления: 2014-01-03