Предельные теоремы

Теорема Пуассона

В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.

Теорема. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна р_i, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей р_i.

Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.

Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.

В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин.

Поставим задачу нахождения предельного закона распределения суммы

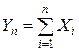
когда число слагаемых п неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова.

В зависимости от условий распределения случайных величин X_i, образующих сумму, возможны различные формулировки центральной предельной теоремы.

Допустим, что случайные величины X_i взаимно независимы и одинаково распределены.

Теорема. Если случайные величины X_i взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием т и дисперсией s², причём существует третий абсолютный момент n₃, то при неограниченном увеличении числа испытаний п закон распределения суммы 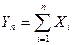неограниченно приближается к нормальному.

При доказательстве этой теоремы Ляпуновым использовались так называемые характеристические функции.

Определение. Характеристической функцией случайной величины Х называется функция

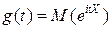
эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 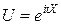, являющейся функцией от случайной величины Х. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.

Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):

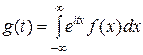
Как видим, данная формула представляет собой не что иное, как преобразование Фурье для функции плотности распределения. Очевидно, что с помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.

Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.

В случае нормального распределения характеристическая функция имеет вид:

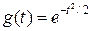
Сформулируем некоторые свойства характеристических функций:

1) Если случайные величины Х и Y связаны соотношением

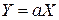
где а – неслучайный множитель, то

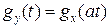
2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.

Случайные величины X_i, рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.

1.6. Теорема Муавра – Лапласа

Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший случай центральной предельной теоремы, известный как теорема Муавра – Лапласа.

Теорема. (Теорема Муавра – Лапласа) Если производится п независимых опытов, в каждом из которых событие А появляется с вероятностью р, то для любого интервала (a, b) справедливо соотношение:

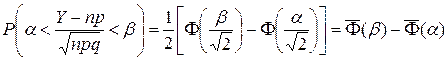
где Y – число появлений события А в п опытах, q = 1 – p, Ф(х) – функция Лапласа, 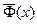- нормированная функция Лапласа.

Теорема Муавра – Лапласа описывает поведение биноминального распределения при больших значениях п.

Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.

Расчёт вероятности попадания значения случайной величины в заданный интервал 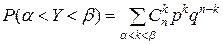при больших значениях п крайне затруднителен. Гораздо проще воспользоваться формулой:

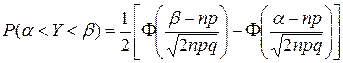
Теорема Муавра – Лапласа очень широко применяется при решении практических задач.

Заключение по лекции:

В лекции мы рассмотрели закон больших чисел. В ходе подготовки к последующей лекции и практическим занятиям вы должны самостоятельно при углубленном изучении рекомендованной литературы и решения предложенных задач дополнить свои конспекты лекций.

Задание на самостоятельную работу

Изучить:

1. Баврин И.И., Матросов В.Л. Высшая математика: Учебник для студентов высших учебных заведений. – М.: Гуманит. изд. центр ВЛАДОС, 2003 г. - 400 с. стр. 394-397.

Дата добавления: 2014-01-03