Свойства эмпирической дисперсии

Рассмотрим основные свойства эмпирической дисперсии, знание которых позволит упростить её вычисление.

1°. Дисперсия постоянной величины равна нулю.

Доказательство этого свойства очевидно вытекает из того, что дисперсия является показателем рассеяния наблюдений вокруг средней арифметической, а средняя арифметическая постоянной равна этой постоянной.

2°. Если все результаты наблюдений уменьшить (увеличить) на одно и то же число с, то дисперсия не изменится.

Доказательство свойств 2° и 3° проведём в предположении, что по результатам наблюдений построен вариационный ряд.

Доказательство. Если все варианты уменьшить на число с, то в соответствии со свойством 2° средней арифметической средняя для измененного вариационного ряда равна (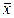 —с), следовательно, его дисперсия

т.е. совпадает с дисперсией первоначального вариационного ряда. Аналогично можно показать, что s²_x+c =s².

Доказанное свойство позволяет вычислять дисперсию не по данным вариантам, а по уменьшенным, (увеличенным) на одно и то же число с, так как дисперсия, вычисленная для измененного ряда, равна первоначальной.

3°. Если все результаты наблюдений уменьшить (увеличить) в одно и то же число k раз, то дисперсия уменьшится (увеличится) в k² раз.

Доказательство. Если все варианты уменьшить в k раз, то, согласно свойству 3^° средней арифметической, средняя для измененного вариационного ряда равна 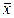/ k, следовательно, его дисперсия

Аналогично можно показать, что .

Это свойство позволяет эмпирическую дисперсию вычислять не по данным вариантам, а по уменьшенным (увеличенным) в одно и то же число k раз. Если дисперсию, вычисленную для измененного ряда, увеличить (уменьшить) в k ² раз, то получим дисперсию для первоначального вариационного ряда.

Следствие. Если все варианты уменьшить (увеличить) в k раз, то среднеквадратическое отклонение уменьшится (увеличится) в число раз, равное k.

Следствие очевидно вытекает из определения среднеквадратического отклонения.

Прежде чем рассматривать следующее свойство дисперсии, докажем теорему.

Теорема. Эмпирическая дисперсия равна разности между средней арифметической квадратов наблюдений и квадратом средней арифметической, т.е.

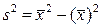. (18)

Доказательство проведём для случая взвешенных средних арифметических, т.е. .

Доказательство. Тождественно преобразуя выражения для дисперсии, имеем

4°, Если ряд наблюдений состоит из двух групп наблюдений, то дисперсия всего ряда равна сумме средней арифметической групповых дисперсий и средней арифметической квадратов отклонений групповых средних от средней всего ряда, причем ' при вычислении средних арифметических весами являются объемы групп.

Пусть 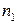и п₂ — число наблюдений соответственно в 1-й и 2-й группах; — средние арифметические для 1-й и 2-й групп наблюдений; —дисперсии для 1-й и 2-й групп наблюдений; и s ²— средняя арифметическая и дисперсия для всего ряда 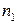+ п₂ наблюдений. Требуется доказать, что

Доказательство. Пусть — ряд наблюдавшихся значений признака, причем к первой группе относятся наблюдения , а ко второй — наблюдения Обозначим символом i порядковый номер наблюдения, попавшего в 1-ю группу, а через j — порядковый номер наблюдения, попавшего во 2-ю группу. На основании теоремы о дисперсии имеем Следовательно, первое слагаемое имеет вид

В соответствии со свойством 4° средней арифметической можно записать . Учитывая последнее равенство, преобразуем второе слагаемое:

Используя найденные выражения для слагаемых, получаем

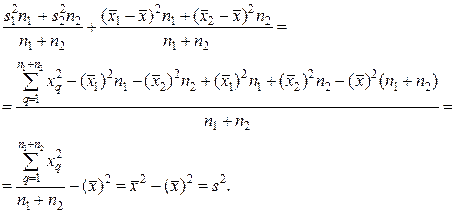
Свойство 4° можно обобщить на случай, когда ряд наблюдений состоит из любого количества k ≥2 групп наблюдений. Введём понятия межгрупповой и внутригрупповой дисперсий.

Если ряд наблюдений состоит из k групп наблюдений, то межгрупповой дисперсией (б²) называют среднюю арифметическую квадратов отклонений групповых средних от средней всего ряда наблюдений 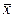, причём весами являются объёмы групп т.е.

Средней групповых дисперсий или внутригрупповой дисперсией называют среднюю арифметическую групповых дисперсий 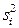, причём весами являются объёмы групп .

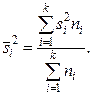
Следствие (свойства 4°). Если ряд наблюдений состоит из k групп наблюдений, то дисперсия всего ряда s² равна сумме внутригрупповой и межгрупповой дисперсий, т.е.

Вычисление дисперсии вариационного ряда непосредственно по формуле (16) приводит к громоздким расчётам, если числовые значения вариантов и соответствующие им частоты велики. Поэтому часто дисперсию вычисляют не по первоначальным вариантам х, а по вариантам х'=(х — с)/k. Зная (дисперсию для измененного ряда), легко вычислить дисперсию s ² для первоначального ряда:

(19)

Действительно, принимая во внимание свойства 3° и 2° дисперсии, получаем

откуда следует, что

Требования к с и k предъявляют те же, что и в упрощенном способе вычисления средней арифметической.

Дата добавления: 2014-01-03