Определение формы связи. Понятие регрессии

Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).

Условное математическое ожидание M(Y\Х=х) случайной переменной Y, рассматриваемое как функция х, т.е. 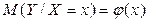, называется функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание M(X\Y=y) случайной переменной X, т.е. 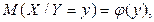называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).

На примере, дискретного распределения найдём функцию регрессии.

Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.

Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек 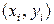на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.

Кривой регрессии Y по X (или Y на X) называют условное среднее значение случайной переменной Y, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.

.

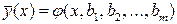Аналогично определяется кривая регрессии X по Y (X на Y):

.

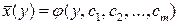Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.

Возникает вопрос: почему для определения кривой регрессии используют именно условное среднее 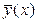? Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. 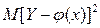. Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является 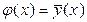. Это следует из свойств минимальности рассеивания около центра распределения 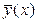. Если рассеивание вычисляется относительно 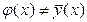, то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как 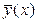, минимизирует среднеквадратическую погрешность прогноза величины Y по X.

Дата добавления: 2014-01-03