Понятие о многомерном корреляционном анализе

Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.

Пусть имеется многомерная нормальная совокупность с m признаками 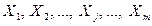. В этом случае взаимозависимость между признаками можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):

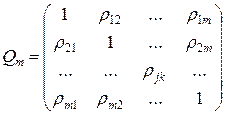(1.14)

где 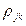— парные коэффициенты корреляции; m — порядок матрицы.

Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для т признаков формула (9.2) принимает вид

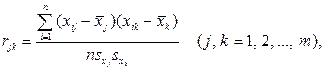(1.15)

где 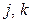— порядковые номера признаков.

Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и т дисперсий, а также т (т —1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2 т + m (т —1)/2 параметров.

В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l -го порядка.

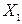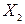Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из т- 2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости междуи при фиксированном значении признака 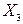. В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.

Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков 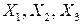. Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков 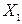и 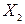при фиксированном значении 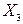выражается через парные коэффициенты корреляции и имеет вид

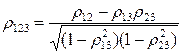. (1.16)

Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из т признаков, частный коэффициент корреляции l -го порядка может быть найден из корреляционной матрицы. Если l = т —2, то рассматривается матрица порядка т, при l < т —2 — подматрица порядка l +2, составленная из элементов матрицы 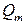, которые отвечают индексам коэффициента частной корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид

.

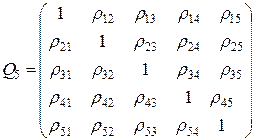Для определения частного коэффициента корреляции второго порядка,

например 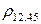, следует использовать подматрицу четвертого порядка, вычеркнув из исходной матрицы Q ₅ третью строку и третий столбец, так как признак Х ₃ не рассматривают.

В общем виде формулу частного коэффициента корреляции l -го порядка (l = т —2) можно записать в виде

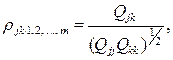(1.17)

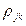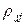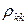где Q_jk — алгебраические дополнения к элементу корреляционной матрицы Q_m; Q_jj и Q_kk — алгебраические дополнения к элементам и корреляционной матрицы Q_m.

Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу Q ₃.

Оценкой частного коэффициента корреляции l -го порядка является выборочный частный коэффициент корреляции l -го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:

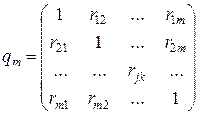(1.18)

Формула выборочного частного коэффициента корреляции имеет вид

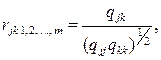(1.19)

где q_jk, q_{j j}, q_kk — алгебраические дополнения к соответствующим элементам матрицы (1.18).

Частный коэффициент корреляции l -го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный по п-l наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.

Множественный коэффициент корреляции. Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции

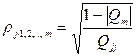, (1.20)

где | Q_m |—определитель корреляционной матрицы Q_m; Q_jj —алгебраическое дополнение к элементу .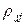

Квадрат коэффициента множественной корреляции 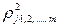называется множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале 0<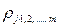< 1. Оценками этих коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно 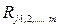и 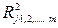. Формула для вычисления выборочного множественного коэффициента корреляции имеет вид

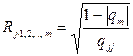(1.21)

где | q_m | —определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; q_jj алгебраическое дополнение к элементу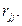

Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.

Дата добавления: 2014-01-03