Алгоритмы в дискретной математике

Конкретная корректно поставленная задача дискретной математики не может встретить принципиальных затруднений в смысле разрешимости. Поставленная на конечном множестве, она всегда может быть решена тривиальным алгоритмом переборного типа. Принципиальным, однако, является число элементарных операций, выполняемых алгоритмом при решении задачи. Каждый класс, рассматриваемых в дискретной математике задач, состоит, как правило, из однотипных задач различной размерности и трудоемкость решения индивидуальной задачи данным алгоритмом в значительной степени определяется её размерностью. Однако, при фиксированной размерности трудоемкость также может колебаться в значительных пределах. Поэтому возможен анализ числа операций как в среднем, так и в наихудшем случае. Анализ в среднем, как правило, более практичен, однако сам процесс усреднения в определенных случаях может быть неоднозначен. Поэтому в теоретических исследованиях чаще используется анализ наихудшего случая.

Если размерность задачи задается числом n (например n чисел или n вершин графа), то будем говорить, что трудоемкость алгоритма есть 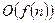(О большое от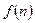), если число операций не превосходит 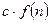, где с – некоторая константа. Для функции 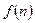есть две существенно различные возможности. Либо это степенная функция, т.е. 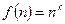, где k – константа. Либо это функция, растущая быстрее любой степени n, например, 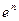. Алгоритмы, трудоемкость которых есть 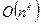, принято считать эффективными. Большая размерность задач не может служить препятствием для решения их на компьютере. Наоборот, экспоненциально растущее число операций ограничивает размеренность решаемых задач даже при использовании самых быстродействующих компьютеров.

Рассмотрим в качестве примера часто встречающуюся на практике задачу линейного упорядочивания массива действительных чисел. Пусть задано n действительных чисел 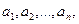которые будем для простоты считать различными. Требуется переписать массив так, чтобы элементы 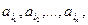были расположены в возрастающем порядке 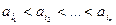. В качестве элементарной операции алгоритма будем рассматривать операцию сравнения двух элементов массива.

Тривиальный алгоритм решения задачи, состоящий в генерировании всех n! перестановок 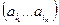и проверке условия монотонности, требует 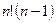сравнений в наихудшем случае и 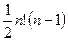сравнений в среднем. Такое число элементарных операций не позволяет осуществить его уже при .

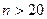Более разумным представляется нахождение минимального элемента массива и помещение его на первое место, затем нахождение минимального элемента в оставшейся части массива и помещение его на второе место и т.д. Данный алгоритм требует 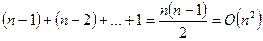сравнений.

Другим разумным подходом является метод вставок. На каждом шаге алгоритма здесь имеется линейно упорядоченное по возрастанию подмножество исходного массива и очередной элемент вставляется в данный линейный порядок. В наихудшем случае данный алгоритм также потребует 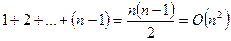сравнений.

Спрашивается, возможно ли линейное упорядочивание массива за меньшее число сравнений? Ответ положителен. Существуют алгоритмы выполняющие упорядочивание за 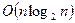сравнений. Одним из них является метод слияния. Пусть имеется два линейно упорядоченных подмножества исходного массива 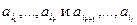. Для нахождения наименьшего элемента в этих двух подмножествах достаточно сравнить 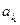с 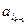. Затем также с помощью одного сравнения находится следующий по порядку элемент и т.д. Этим достигается упорядочивание за 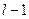сравнений.

Будем для простоты считать число n степенью двойки n =2^m. Разобьем n элементов на пары и упорядочим каждую пару. Затем сольем пары в четверки и упорядочим каждую четверку. Затем четверки сольем в восьмерки и т.д. На каждом уровне при слиянии всего требуется 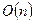сравнений. Умноженное на число уровней 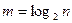, это дает 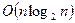сравнений.

Для некоторых экстремальных задач в теории графов известны эффективные алгоритмы решения. К таким задачам относятся, в частности, рассматриваемые ниже задачи о минимальном остовном дереве и о минимальном пути между двумя вершинами. Для ряда других задач, в частности, задачи нахождения гамильтонова цикла минимальной длины (задача коммивояжера) эффективных алгоритмов неизвестно. Широко распространенным является мнение, что широкий класс дискретных экстремальных задач не допускает эффективного решения, хотя это и не удалось доказать. В тех случаях, когда эффективный алгоритм неизвестен, задачи небольшой размерности могут быть решены с помощью метода «ветвей и границ», т.е. сокращенного перебора. Этот метод будет ниже продемонстрирован на примере задачи коммивояжера.

Тест

1. Какое из следующих соотношений имеет место а) 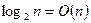; б) 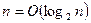; в) ни то, ни другое.

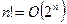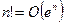2. Какое из следующим соотношений имеет место а) ; б) ; в) .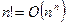

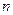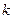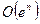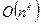3. Пусть - размерность задачи, - константа. Алгоритм считается эффективным, если его трудоемкость есть а) ; б) ; в) .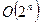

Дата добавления: 2014-01-03