
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Потоки в сетях
|
|
|
|
Рассматриваемые здесь сети возникли как математические модели реальных коммуникационных и транспортных сетей. Сеть можно представлять себе как систему, транспортирующую определенный продукт из одной точки в другую и имеющую ограничения на пропускные способности. Такими сетями являются нефте и газопроводы, железнодорожные и автомобильные сети.
Математическая модель сети определяется следующим образом. Задан взвешенный ориентированный граф  , веса
, веса  на дугах которого являются целыми положительными числами и называются пропускными способностями дуг. В графе выделены две вершины:
на дугах которого являются целыми положительными числами и называются пропускными способностями дуг. В графе выделены две вершины:  , называемая источником, и
, называемая источником, и 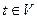 , называемая стоком. Допустимым потоком из s в t величины F называется заданная на дугах графа неотрицательная функция
, называемая стоком. Допустимым потоком из s в t величины F называется заданная на дугах графа неотрицательная функция  , удовлетворяющая следующим условиям
, удовлетворяющая следующим условиям

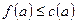 для всех
для всех 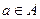 .
.
Говоря неформально, поток рождается в вершине s и изчезает в вершине t, а во всех остальных вершинах сети количество входящего потока равно количеству выходящего. Кроме того, на каждой дуге поток не превосходит её пропускной способности.
Понятие разреза является важнейшим в развиваемой далее теории. Пусть 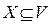 ,
,  ,
,  ,
,  . Разрезом
. Разрезом  , отделяющим вершины s и t, называется множество дуг, идущих из
, отделяющим вершины s и t, называется множество дуг, идущих из  и
и 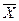 . Пропускная способность разреза с
. Пропускная способность разреза с  определяется как
определяется как
 .
.
Рассмотрим в качестве примера сеть, изображенную на рисунке, где числа около дуг обозначают их пропускную способность.

Пусть  . Тогда
. Тогда 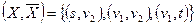 ,
,  .
.
Определим поток через разрез  как разность между суммой потоков по дугам из
как разность между суммой потоков по дугам из  в
в 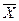 и суммой потоков по дугам из
и суммой потоков по дугам из 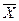 в
в 
 .
.
Лемма. Поток через любой разрез, отделяющий s и t, равен величине потока в сети  .
.
Доказательство. Утверждение, очевидно, справедливо, если  . Допустим, что оно верно для некоторого разреза
. Допустим, что оно верно для некоторого разреза  . Докажем его справедливость для разреза
. Докажем его справедливость для разреза  , где
, где  ,
,  , т.е. разрез
, т.е. разрез  получен из разреза
получен из разреза  перенесением одной вершины из
перенесением одной вершины из  в
в  .
.
|
|
|
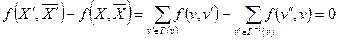 .
.
Этим справедливость леммы доказана.
Так как 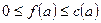 ,то в качестве следствия получаем, что максимальная величина потока не превосходит минимальной пропускной способности разреза, отделяющего s и t. Оказывается, что здесь, на самом деле, всегда имеет место равенство, что неудивительно, т.к. минимальный разрез воспринимается как «узкое место» сети.
,то в качестве следствия получаем, что максимальная величина потока не превосходит минимальной пропускной способности разреза, отделяющего s и t. Оказывается, что здесь, на самом деле, всегда имеет место равенство, что неудивительно, т.к. минимальный разрез воспринимается как «узкое место» сети.
Теорема. (Ford, Fulkerson, 1956). Для любой сети максимальная величина потока из s в t равна минимальной пропускной способности разреза, отделяющего s и t.
Доказательство проведем конструктивно, т.е. укажем алгоритм, который за конечное число шагов строит допустимый поток, равный по величине пропускной способности некоторого разреза.
Выберем в качестве начального допустимого потока нулевой по всем дугам поток и будем его последовательно наращивать, увеличивая величину потока на каждом шаге на  . За конечное число шагов будет, таким образом, построен максимальный допустимый поток. Наращивание потока будет осуществляться следующим образом. Пусть задан некоторый допустимый поток. Покажем, как можно его увеличить или указать разрез, пропускная способность которого равна величине потока. Ищем такой путь из s в t, в котором можно идти по дугам как в прямом, так и в обратном направлении, но дуги, проходимые в прямом направлении, должны быть ненасыщенны
. За конечное число шагов будет, таким образом, построен максимальный допустимый поток. Наращивание потока будет осуществляться следующим образом. Пусть задан некоторый допустимый поток. Покажем, как можно его увеличить или указать разрез, пропускная способность которого равна величине потока. Ищем такой путь из s в t, в котором можно идти по дугам как в прямом, так и в обратном направлении, но дуги, проходимые в прямом направлении, должны быть ненасыщенны  , а дуги, проходимые в обратном направлении, должны быть нагружены
, а дуги, проходимые в обратном направлении, должны быть нагружены  . Если такой путь найден, то ищем минимум по всем дугам пути из величин
. Если такой путь найден, то ищем минимум по всем дугам пути из величин  для дуг, проходимых в прямом направлении и
для дуг, проходимых в прямом направлении и  для дуг, проходимых в обратном направлении. Пусть этот минимум равен
для дуг, проходимых в обратном направлении. Пусть этот минимум равен  . Строим новый поток, увеличивая поток по дугам в прямом направлении на
. Строим новый поток, увеличивая поток по дугам в прямом направлении на 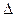 и уменьшая поток по дугам в обратном направлении на туже величину. (Потоки по дугам не принадлежащим пути, остаются без изменения).
и уменьшая поток по дугам в обратном направлении на туже величину. (Потоки по дугам не принадлежащим пути, остаются без изменения).
|
|
|
Новый поток будет, как легко понять, допустимым и иметь величину на 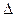 единиц больше прежней. Если же вершина t недостижима подобным образом из s, то это значит, что существует множество вершин
единиц больше прежней. Если же вершина t недостижима подобным образом из s, то это значит, что существует множество вершин  , недостижимых из s, причем
, недостижимых из s, причем  ,
,  . Так как из множества
. Так как из множества  нельзя перейти в множество
нельзя перейти в множество 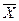 определенным выше образом, то все ребра из
определенным выше образом, то все ребра из 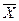 в
в  ненагружены. Поэтому поток
ненагружены. Поэтому поток  через разрез
через разрез  , равный, по доказанной лемме, величие потока в сети, равен пропускной способности разреза
, равный, по доказанной лемме, величие потока в сети, равен пропускной способности разреза  . Этим завершается доказательство.
. Этим завершается доказательство.
Проиллюстрируем процесс наращивания потока на примере. Первая цифра в скобках над каждой дугой обозначает пропускную способность, вторая – поток по дуге.
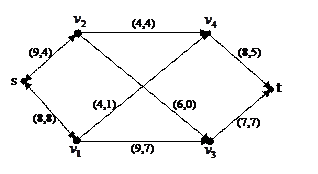
Увеличивающим поток путем является 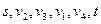 ,
,  .
.
Новый поток примет вид
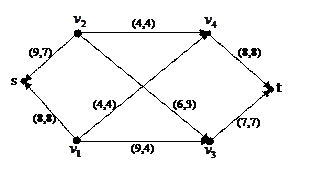
Попробуем снова найти увеличивающий поток путь. Из s можно попасть в 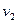 , из
, из 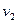 - в
- в 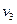 , из
, из 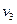 - в
- в 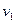 . Никаких других вершин сети из s достичь не удается. Поэтому
. Никаких других вершин сети из s достичь не удается. Поэтому  ,
, 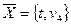 и
и  - разрез с пропускной способностью 4+4+7=15, равной величине потока в сети. Следовательно данный поток является максимальным.
- разрез с пропускной способностью 4+4+7=15, равной величине потока в сети. Следовательно данный поток является максимальным.
При поиске увеличивающего поток пути вершину, которую удается достичь, следует помечать номером вершины, из которой в нее попали. Это позволяет по достижении вершины t легко восстановить увеличивающий поток путь. Поэтому данный алгоритм для нахождения максимального потока часто называют алгоритмом пометок Форда и Фалкерсона.
В процессе поиска увеличивающего пути из каждой вновь помеченной вершины просматриваются все инцидентные её дуги. При этом каждая дуга сети может просматриваться максимум дважды: со стороны начала и со стороны конца. Поэтому трудоемкость поиска увеличивающего пути есть  . Для получения трудоемкости алгоритма в целом это число следует умножить на число итераций, которое заведомо не превосходит величины максимального потока. Поэтому, если пропускные способности дуг ограничены, трудоемкость алгоритма пометок есть
. Для получения трудоемкости алгоритма в целом это число следует умножить на число итераций, которое заведомо не превосходит величины максимального потока. Поэтому, если пропускные способности дуг ограничены, трудоемкость алгоритма пометок есть 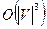 . Однако и в случае произвольных пропускных способностей за счет более тщательной реализации алгоритма удается достичь трудоемкости
. Однако и в случае произвольных пропускных способностей за счет более тщательной реализации алгоритма удается достичь трудоемкости 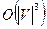 .
.
Теорема Форда – Фалкерсона о максимальном потоке и минимальном разрезе может быть использована для получения ряда результатов, относящихся к математическим моделям спроса и предложения. Пусть имеется k поставщиков  некоторого товара и m его потребителей
некоторого товара и m его потребителей 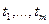 . Для каждого поставщика
. Для каждого поставщика 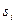 известно количество товара
известно количество товара  , которое он в состоянии поставить на рынок, а также то подмножество потребителей, которым он может его направить. Для каждого потребителя
, которое он в состоянии поставить на рынок, а также то подмножество потребителей, которым он может его направить. Для каждого потребителя  задано необходимое ему количество товара. Спрашивается, при каких условиях может быть удовлетворен спрос всех потребителей?
задано необходимое ему количество товара. Спрашивается, при каких условиях может быть удовлетворен спрос всех потребителей?
|
|
|
Теорема (о спросе и предложении). Для удовлетворения спроса необходимо и достаточно, чтобы для каждого подмножества потребителей  было выполнено условие
было выполнено условие
 ,
,
где Г-1( ) – множество поставщиков, поставляющих товар хотя бы одному потребителю из подмножества
) – множество поставщиков, поставляющих товар хотя бы одному потребителю из подмножества  .
.
Доказательство. Ясно, что условие теоремы является необходимым. Покажем его достаточность. Рассмотрим двудольный орграф  , где
, где 
 ,
, 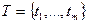 , а дуга
, а дуга  в том и только в том случае, если поставщик
в том и только в том случае, если поставщик 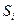 может направлять товар потребителю
может направлять товар потребителю  . Преобразуем орграф
. Преобразуем орграф 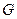 в сеть, добавив источник
в сеть, добавив источник  и сток
и сток 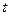 и проведя дуги от
и проведя дуги от  ко всем
ко всем 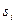 и от всех
и от всех  к
к 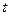 , как показано на рисунке
, как показано на рисунке

Дугам 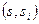 припишем пропускные способности
припишем пропускные способности 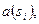
 . Дугам
. Дугам 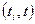 припишем пропускные способности
припишем пропускные способности  ,
,  . Пропускные способности дуг
. Пропускные способности дуг  будем считать бесконечными. Тогда минимальный разрез может содержать только дуги с конечными пропускными, т.е. дуги
будем считать бесконечными. Тогда минимальный разрез может содержать только дуги с конечными пропускными, т.е. дуги 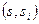 и
и  . Если минимальный разрез равен
. Если минимальный разрез равен
 ,
,
то по теореме о максимальном потоке и минимальном разрезе существует поток, удовлетворяющий спрос всех потребителей.
Если же имеется разрез меньшей пропускной способности, то он обязан содержать и дуги вида 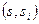 Пусть
Пусть  множество поставщиков, в которых заканчиваются дуги вида
множество поставщиков, в которых заканчиваются дуги вида 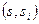 минимального разреза,
минимального разреза, 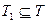 - множество потребителей, в которых начинаются дуги минимального разреза вида
- множество потребителей, в которых начинаются дуги минимального разреза вида  . Имеем
. Имеем
 ,
,
но  , поэтому
, поэтому  . Имеем далее
. Имеем далее

откуда  ,
,
и для множества  оказывается невыполненным условие теоремы. Поэтому множество дуг
оказывается невыполненным условие теоремы. Поэтому множество дуг  ,
,  образует минимальный разрез и все они насыщаются при максимальном допустимом потоке в сети.
образует минимальный разрез и все они насыщаются при максимальном допустимом потоке в сети.
Как следует из алгоритма пометок, всегда существует целочисленный максимальный поток. В частности, если все дуги имеют единичные пропускные способности, то существует максимальный поток, на каждой дуге равный нулю или единице. Это замечание лежит в основе применения потоковых алгоритмов к решению комбинаторных задач. В качестве подобного примера вернемся к задаче о максимальном паросочетании в двудольном графе и покажем, как она может быть решена с помощью потокового алгоритма.
|
|
|
Пусть задан двудольный граф 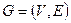 , где
, где 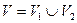 ,и в нем требуется найти наибольшее паросочетание. Преобразуем граф в сеть, введя две дополнительные вершины s и t. От вершины s проведем дуги ко всем вершинам множества
,и в нем требуется найти наибольшее паросочетание. Преобразуем граф в сеть, введя две дополнительные вершины s и t. От вершины s проведем дуги ко всем вершинам множества 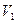 , а из всех вершин множества
, а из всех вершин множества 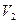 проведем дуги к t. Ребра графа сделаем дугами, придав им направление от
проведем дуги к t. Ребра графа сделаем дугами, придав им направление от 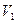 к
к 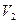 . Пропускные способности всех дуг сети положим равными единице. Такое преобразование двудольного графа в сеть схематически показано на рисунке.
. Пропускные способности всех дуг сети положим равными единице. Такое преобразование двудольного графа в сеть схематически показано на рисунке.

Существует взаимно однозначное соответствие между паросочетаниями в графе и (0-1) – потоками в сети, устанавливаемое тем, что поток пускается по ребрам паросочетания. При этом число ребер в паросочетании равно величине потока в сети. Поэтому максимальному (0-1) – потоку соответствует наибольшее паросочетание.
Сделанное замечание позволяет дать матричный аналог теоремы Форда –Фалкерсона. Рассмотрим прямоугольную матрицу из нулей и единиц. Будем называть её строки и столбцы «рядами». Подмножество единиц назовем независимым, если никакие две единицы не стоят в одном ряду. Поставим вопрос, какое минимальное число рядов нужно вычерпнуть, чтобы зачеркнуть все единицы? Ясно, что минимальное число рядов не меньше максимального числа независимых единиц. Оказывается, что в действительности всегда имеет место случай равенства. Это сразу следует из теоремы Форда – Фалкерсона, если с матрицей связать двудольный граф, одна доля которого соответствует строкам, а другая – столбцом матрицы. При этом максимальное число независимых единиц будет соответствовать наибольшему паросочетанию в графе или максимальному потоку в полученной из него сети, а минимальное число вычеркиваемых рядов – минимальному разрезу.
В качестве примера рассмотрим приведенную на рисунке матрицу (5´5).
| ï* | ï | ï | ||
| ï* | ï | |||
| ï | ï | ï* | ||
| ï* | ||||
| ï | ï |
Все её единицы будут вычеркнуты, если вычеркнуть 4 ряда: первую и третью строки и второй и четвертый столбцы. Четыре независимые единицы отмечены звездочками.
Отметим также, что теорема Холла о системе различных представителей есть дискретный вариант теоремы о спросе и предложении.
Тест.
1. Какова трудоемкость нахождения увеличивающего поток пути в алгоритме пометок?
а) 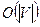 ; б)
; б) 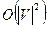 ; в)
; в) 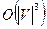 .
.
2. Какова трудоемкость потокового алгоритма? а) 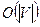 ; б)
; б) 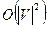 ; в)
; в) 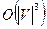 .
.
3. Максимальный поток а) всегда является целочисленным; б) всегда может быть выбран целочисленным; в) может оказаться невозможным выбрать целочисленным.
Глава III. Кодирование
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1079; Нарушение авторских прав?; Мы поможем в написании вашей работы!