Второй замечательный предел. Числовая последовательность и ее предел

Рассмотрим функцию, областью определения которой является множество натуральных чисел. Такая функция называется функцией натурального аргумента или последовательностью. Значения этой функции называются членами последовательности.

О.3.1. Числовой последовательностью называется функция натурального аргумента .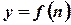

Т.е. это функция, заданная на множестве натуральных чисел.

Члены числовой последовательности обычно располагаются в порядке возрастания аргумента

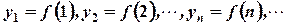
Кратко числовая последовательность обозначается следующим образом: .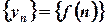

Пример. Дана числовая последовательность .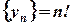

Найти четыре первых членов последовательности.

Получим: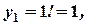

.

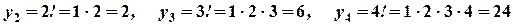Введем понятие предела последовательности.

О.3.2. Число 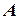называется пределом последовательности 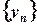, если для любого 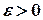, найдется такое натуральное число , что для всех членов последовательности, номер которых 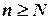, выполняется неравенство .

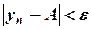Определение предела последовательности аналогично определению предела функции при .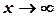

Для функции условие 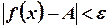выполняется для всех действительных значений 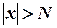, а для последовательности неравенство 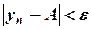выполняется при всех натуральных числах .

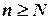Геометрический смысл. Неравенство 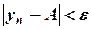равносильно неравенствам .

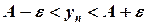Изобразим члены последовательности точками плоскости 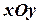с координатами .

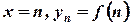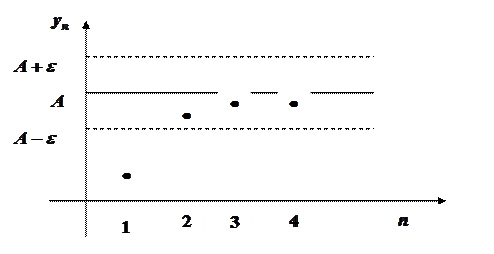
Геометрический смысл предела: если последовательность имеет предел 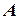, то каково бы ни было 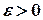, найдется такое , что все точки, изображающие члены последовательности с номерами 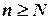(на рисунке 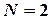) попадут в полосу, ограниченную прямыми .

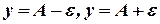Все теоремы о пределах функции справедливы и для последовательности.

О.3.4. Последовательность называется возрастающей, если с увеличением 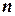её члены увеличиваются, т.е.

.

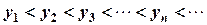Если с увеличением 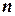члены последовательности убывают, т.е.

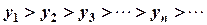, то последовательность называется убывающей.

О.3.5. Последовательность называется ограниченной, если найдется такое число 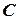, что для всех натуральных чисел 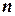выполняется неравенство

.

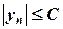Т.3.1. (достаточный признак существования предела последовательности). Всякая возрастающая (убывающая) ограниченная последовательность имеет предел. Если последовательность возрастает и ограничена, то она имеет предел.

Дата добавления: 2014-01-03