Итерационные методы решения СЛАУ

Алгоритм

Метод Ньютона

Одним из наиболее эффективных методов нахождения корней уравнения (2.1) является метод Ньютона, расчетное соотношение которого можно получить, используя два различных подхода.

Метод касательных. Допустим, найдено некоторое начальное приближение 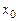к решению уравнения. В точке с координатами проводим касательную к графику функции , затем находим точку пересечения этой касательной с осью абсцисс – это будет первое приближение (Рис.2.4). Строя касательную в точке и находя точку ее пересечения с осью 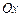, определяем второе приближение 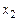. Продолжая этот процесс, получаем последовательность приближений , ,..., ,... к корню уравнения (2.1).

Уравнение касательной, проведенной к графику функции в точке , будет иметь вид

.(2.19)

Согласно описанной последовательности следующее приближение получается при , т.е. из уравнения

.(2.20)

Откуда

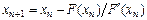.(2.21)

Именно благодаря такой геометрической интерпретации этот метод иногда называют методом касательных.

Рис.2.4. Метод Ньютона

Метод линеаризации. Если определена некоторая достаточно малая область нахождения решения, то любую сложную кривую в этой области приближенно можно заменить на прямую, т.е. провести линеаризацию функции в данной области. Используя эту процедуру, можно свести решение исходного нелинейного уравнения к последовательному решению линейных уравнений.

Пусть приближение найдено, тогда, представляя функцию в окрестности точки в виде разложения в ряд по формуле Тейлора, получаем

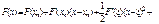,(2.22)

где – некоторая точка отрезка . Заменяя функцию ее главной линейной частью, находим решение (2.1) в виде аналогичном (2.21), согласно предыдущему анализу это будет 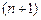приближение.

Метод Ньютона можно рассматривать как один из вариантов метода простой итерации. В самом деле, если принять

,(2.23)

итерационная формула (2.21) совпадет с итерационной формулой (2.10). При этом вопрос о сходимости метода Ньютона будет вытекать из сходимости метода простой итерации. Необходимо отметить, что из всех итерационных формул метод Ньютона обладает наибольшей скоростью сходимости. Критерий окончания итерационного процесса также будет определяться соотношением (2.18).

К сожалению, метод Ньютона, отличаясь простотой, логической стройностью и высокой скоростью сходимости, имеет ряд существенных недостатков. К наиболее важным из них относятся два. Во-первых, для реализации метода необходимо на каждом шаге вычислять производную. Часто сделать это аналитически весьма непросто, а определять приближения с требуемой точностью достаточно трудно. Во-вторых, метод Ньютона обладает локальной сходимостью. Это означает, что областью его сходимости является только некоторая (иногда достаточно малая) окрестность решения. Если начальное приближение выбрано плохо, то в некоторых случаях возможно появление расходящейся последовательности приближений.

Для преодоления первого недостатка используют некоторые модифицированные методы, избегая непосредственного вычисления производной. Чтобы расширить область возможных начальных приближений, метод Ньютона используют совместно с медленно сходящимися методами, но дающими гарантированную сходимость (например, методом дихотомии).

1. Локализуем корень.

2. Выбираем начальное приближение .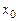

3. Вычисляем производную в точке .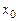

4. Вычисляем следующее приближение по формуле (2.21).

В качестве примера программной реализации возьмем уравнение (2.3). Будем искать решение с точностью не более на отрезке , где, как было показано, находится только один корень. С учетом соотношение (2.21), получим следующую итерационную формулу:

.(2.24)

3. Решение систем линейных алгебраических уравнений

В вычислительной линейной алгебре обычно выделяют четыре основных типа задач:

1. решение систем линейных алгебраических уравнений;

2. нахождение собственных значений и собственных векторов;

3. вычисление определителей;

4. нахождение обратных матриц.

В основе решения этих задач лежит анализ системы линейных алгебраических уравнений (СЛАУ), которая имеет следующий вид

(3.1)

Ее можно представить в матричном виде

,(3.2)

где

, , ,при этом предполагается,что .

В СЛАУ (3.1) представим матрицу в виде

,тогда система приобретает вид или .

(3.13)

Рассмотрим последовательность векторов 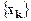, удовлетворяющую условию

,(3.14)

где (), и вектор 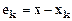, где 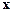– решение заданной системы.

Вычтя из равенства (3.13) равенство (3.14), получим , т.е. . Поэтому ,

…,

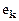и, если множество стремится к нулю, то итерационный процесс (3.14) сходится и пределом последовательности 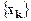является вектор 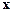– решение данной системы.

Итерационный метод (3.14) сходится тогда и только тогда, когда каждое собственное значение 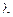матрицы удовлетворяет неравенству .

Скорость сходимости зависит от спектрального радиуса матрицы , который определяется равенством .

1. Метод простой итерации. Метод простой итерации сводится к представлению матриц и в следующем виде:

, ,

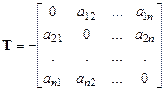Тогда матрицу 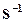можно вычислить следующим образом

.

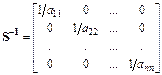Из неравенства (3.14) следует, что

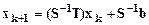. (3.15)

Соотношение (3.15) определяет алгоритм вычисления.

Пример. Решить методом простой итерации систему уравнений

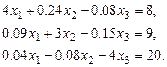Выразим из первого уравнения, 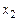– из второго и – из третьего. Получим

то есть

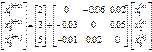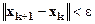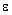где . Используя это соотношение, можем последовательно вычислять векторы . Решение будет найдено, когда , где – некоторая заданная точность решения.. Метод Зейделя. Матрицы и определяются следующим образом:

, ,

где – нижняя треугольная матрица, а – верхняя (строго) треугольная матрица.

Применяя метод Зейделя к решению рассмотренной выше системы, получим следующие соотношения

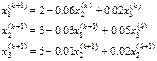
для членов последовательности .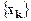

Дата добавления: 2017-01-14