Метод наименьших квадратов для регрессионного анализа

Пусть

Примеры решение переопределенной СЛАУ методом наименьших квадратов

(6.21)система, содержащая m линейных алгебраических уравнений и n неизвестных, при этом m > n, то есть число уравнений превышает число неизвестных. Тогда – матрица системы размера m n, а x – n -мерный вектор неизвестных, b – n-мерный вектор свободных членов. Предположим, что система (6.21) несовместна. Это означает, что не существует вектора x, размерности (n 1), для которого , иначе 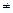0. Задача состоит, в том, чтобы минимизировать норму невязки

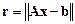.(6.22)

Эта величина есть расстояние от точки 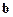размерности m 1 до точки , лежащих в пространстве столбцов матрицы = , здесь – вектор размерности m 1. Тогда , или

.

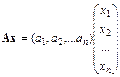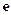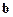Правая часть выражения (6.21) является линейной комбинацией столбцов матрицы с коэффициентами . Таким образом, задача минимизации невязки равносильна отысканию точки , ближайшей к точке по сравнению с остальными точками пространства столбцов матрицы . Из этого следует, что вектор невязки должен быть ортогонален этому пространству. Любой вектор в пространстве столбцов матрицы – это вектор

= .

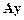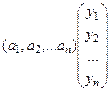Ортогональность векторов 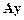и означает равенство нулю их скалярного произведения. Поэтому =0, то есть =0. Учитывая свойство транспонированных матриц, получаем

= .

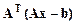Поэтому =0 и, поскольку вектор – произвольный, то =0. Раскрывая скобки, получаем 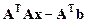=0, откуда следует равенство:

. (6.23)

Решая это уравнение, получаем решение поставленной задачи.

Если столбцы матрицы – линейно независимы (ранг матрицы равен n), то матрица обратима и искомое решение выражается формулой:

.(6.24)

Для начала рассмотрим линейную регрессию от одной переменной. Пусть имеются результаты измерений двух величин 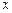и , предполагается, что они связаны линейной зависимостью

.(6.25)

При этом ошибка измерения является некоторой случайной величиной, а ее среднее значение равно нулю. Так как результаты не ложатся на прямую, то необходимо построить наилучшую прямую проходящую наиболее близко к каждой из этих точек. Это типичная задача обработки измерений.

Для нахождения неизвестных коэффициентов используют метод наименьших квадратов, а именно минимизируют функционал вида

.

(6.26)

Необходимым условием минимума будет выполнение условий

.

(6.27)

В результате получим

, (6.28)

где средние значения 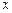и определяются по формулам

. (6.29)

Формулы (6.28) позволяют построить график прямой, называемой регрессией на 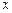, которая дает представление о зависимости. В дополнение к ней обычно строят и регрессию 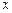на , модель которой аналогична (6.25), только в качестве независимой переменной используют . Таким образом, получают две пересекающиеся в точке 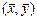прямые, при этом большинство результатов измерений лежит именно между ними. Более того, во многих случаях удается линеаризовать исходную зависимость и рассматривать ее относительно некоторых новых переменных, которые образуют линейную связь. Например, для функции берут новые переменные 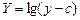и получают зависимость вида .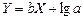

В общем случае, если регрессия на 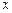отличается от линейной, рассматривают линейную по параметрам регрессионную модель вида

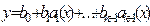, (6.30)

где – известные функции, а неизвестные параметры. Пусть имеется 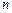наблюдений , которые являются результатом реализации случайной величины

(6.31)

здесь 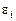– случайные независимые друг относительно друга и распределенные по нормальному закону ошибки наблюдений. Необходимо отметить, что система уравнений относительно неизвестных является типичной пере- или недоопределенной задачей и должна решаться методом наименьших квадратов.

По методу наименьших квадратов в качестве оценок принимают значения , дающие минимум функции

(6.32)

Из необходимых условий минимума следует, что оценки являются решениями алгебраической системы уравнений

(6.33)

Данную систему уравнений часто называется нормальной системой. В матричных обозначениях она имеет вид

,(6.34)

где 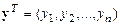– 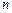-вектор наблюдений, – -вектор оценок параметров, – регрессионная -матрица.

При условии, что матрица – невырожденная, решение (6.33) можно записать в виде

(6.35)

Часто в качестве функций принимают степенные функции, т.е. . В этом случае регрессионная матрица имеет вид

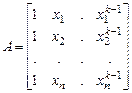. (6.36)

Уравнение для нахождения неизвестного вектора параметров 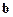будет иметь вид

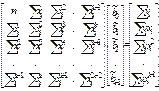.(6.37)

Эту систему уравнений можно решить либо методом Гаусса, если она не слишком большой размерности, либо итерационными методами.

Проведем обработку экспериментальных данных (26 измерений) представленных на рисунке 6.1 «звездочками». Из рисунка видно, что зависимость переменных друг от друга является нелинейной. Очевидно, что интерполяционную кривую строить не имеет смысла. Аппроксимируем наши данные полиномом третьей степени, т.е. представим нашу кривую в виде .

Основная задача определить коэффициенты 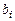. Для расчетов необходимо задать массивы данных 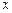и , построим программу, используя соотношение

Дата добавления: 2017-01-14