Одномірна оптимізація без обмежень

Задача оптимізації, в якій величина критерію залежить від одного фак­тору, при відсутності обмежень відноситься до класу одномірної безумов­ної оптимізації. Це прості і досить поширені в оптимізації інженерних рішень задачі.

Переходячи до методів одномірної оптимізації, нагадаємо правила знаходження максимуму і мінімуму за допомогою похідних від функцій, що диференціюються (див. рис. 7.1 а і табл. 7.2). У точках мінімуму і мак­симуму відбувається зміна знаку першої похідної f'(х), в той час як у точці перегину функції х_п знак похідної не змінюється. Отже, за допомогою по­хідних функції, що диференціюється, ми можемо виявити точки екстре­мумів. Якщо функція f (х) унімодальна, то цього достатньо для вирішення оптимізаційної задачі. Якщо ж функція має декілька мінімумів або макси­мумів, то для визначення локального чи глобального мінімуму необхідно порівняти значення функцій у відповідних точках, тобто порівняти f (х₀) і f (х*) у наведеному прикладі (див. рис. 7.1 а).

Таблиця 7.2 Характерні значення функції

Значення похідних функції	Точка	Значення функції
Перша похідна f'(х) = 0	x 0	Локальний мінімум
	xт	Локальний максимум
	x^*	Глобальний мінімум
	хn	Перегин функції
f΄(x) = 0, друга похідна f "(х) < 0	xт	Локальний максимум
f'(х) = 0,f΄'(х)>0	x 0	Локальний мінімум
	x^*	Глобальний мінімум

Приклад: Нехай задана певна кількість листового матеріалу, з якого необхідно виготовити бункер-нагромаджувач зерна циліндричної форми. Потрібно визначити радіус r і висоту h циліндра, при яких об’єм бункера буде максимальним (V _б →mах).

З урахуванням площі відходів металу S₀ та того, що у відходи йде лише метал при вирізанні дна (круга) із квадрату, що має сторону 2r поверхня бункера S_б буде рівною:

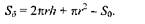(7.7)

Висоту циліндра виразимо через об’єм бункера V_б:

(7.8)

Підставивши вираз (7.8) у формулу (3.7), об’єм бункера можна записати у вигляді функції від однієї змінної — радіуса r:

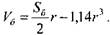(7.9)

Величина S_б регламентується заданою кількістю металу, тобто є для конкретного випадку постійною. Екстремум функції (7.9) знайдемо прирівнюючи до нуля її першу похідну:

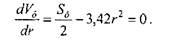(7.10)

Звідки

Оскільки друга похідна d ² V_б/dr ²=-6,48 r, тобто менше нуля, то точка екстремуму відповідає максимуму об’єму (V_6таx). А у зв’язку з тим, що функція (7.9) унімодальна, то значення r з формули (7.10) буде рішенням оптимізаційної задачі.

Висоту бункера при заданих значеннях поверхні S_б і радіусу r знаходимо з формули (7.7):

(7.11)

Про користь оптимізації можна судити з числового прикладу, що наведений у табл. 7.3.

Як видно з таблиці, при відхиленні від оптимального значення r_опт на 0,5 м об’єм бункера знижується на 1,3 м³, що може суттєво впливати на функціональні та економічні показники виробничого процесу.

Таблиця 7.3. Залежність об’єму циліндричного бункера від радіусу при S_б= 16 м²

Радіус r, м	Висота h, м	Об’єм Vб, м^3
1,00	2,19	6,86
1,52	1,13	8,16
2,00	0,55	6,88

Метод знаходження оптимуму з використанням похідних обмежуєть­ся умовою диференційованості функції. Крім того, можливі випадки, коли функція f(х) включає члени з високими показниками степеня (вище трьох) і аналітичний розв’язок рівняння f’(х)=0 може бути ускладненим. В таких випадках використовуються наближені методи послідовного пошуку опти­муму, які спираються на числові методи розв’язку.

При застосуванні числових методів послідовного виключення інтерва­лів точка мінімуму (максимуму) знаходиться шляхом визначення і порів­няння значень функцій f (х) у заданому інтервалі [а; b], послідовного зву­ження інтервалу пошуку до знаходження оптимуму із заданою точністю.

Найбільш ефективним з точки зору простоти реалізації та процедури обчислень є пошук оптимуму методом «золотого перетину». Його суть роз­глянемо на графічному прикладі (рис. 7.3).

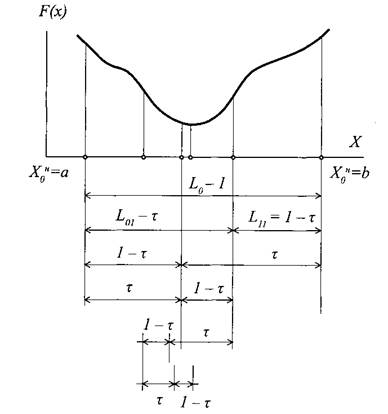
Рис. 7.3. Схема ітерацій при оптимізації методом «золотого перетину».

Попередньо встановлюється початковий інтервал [а; b], в якому перед­бачається наявність мінімуму. Умовою застосування методу «золотого пе­ретину» є унімодальність функції на заданому інтервалі.

Далі визначають значення f(х) у точках х^н₀ = а та х^в₀ = b, тобто початковий інтервал буде рівним х^в₀ - х^н₀ = L₀. Інтервал [а; b] поділяють на два відрізки в пропорції золотого перетину, при якій відношення цілого відрізка до його більшої частини дорівнює відношенню більшої частини до меншої, тобто

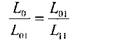(7.12)

Прийнявши початковий інтервал L₀= 1, a L₀₁=τ, можемо записати:

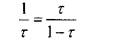(7.13)

Додатнім коренем цього квадратного рівняння буде:

Отже, визначивши значення х₁ та х₂, розраховують для них відповідні значення функції f (х₁) та f (х₂) і порівнюють їх з метою скорочення інтер­валу пошуку: якщо f (х₁) < f (х₂), то приймають новий інтервал (х^в₀, x₂); коли f (х₁) > f (х₂) приймають (x₁, х^в₀).

Таким чином, на першому звуженні інтервалу виключається відрізок (1-τ). Наступні ітерації повторюють описані вище процедури визначення точок всередині інтервалу, порівняння значень функцій f(х_i) в цих точках і перехід до нового інтервалу (див. рис. 7. 3). Остання ітерація встановлю­ється або виходячи із заданого числа наближень, або з відносної точності значення функції f (х*). Часто буває доцільно застосовувати обидва крите­рії одночасно.

Метод «золотого перетину» набув широкого застосування через простий, і ефективний алгоритм пошуку оптимуму, зручності його реаліза­ції на ЕОМ.

При пошуках оптимуму функцій з однією змінною часто зручніше за­мість аналітичного розв’язку побудувати графік функції і знайти значен­ня аргументу, яке відповідає мінімуму або максимуму функції. У таких випадках можна встановити оптимум для функцій дискретних і з розри­вами, а також при порушенні умови унімодальності. У більшості випадків неточності, що притаманні графічним методам, знаходяться в допусти­мих для прийняття інженерних рішень межах.

Дата добавления: 2015-07-13