Решение систем линейных уравнений с помощью определителей. Формулы Крамера

Задачи для самостоятельного решения

Задача 1. Вычислить определители:

1) 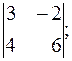2) 3) 4) .

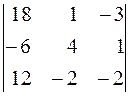Задача 2. Вычислить определители, разложив их по элементам первого столбца:

1) 2)

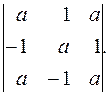
Задача 3. Найти 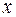из уравнений:

1) 2)

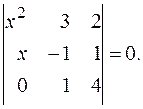
I) Система двух линейных неоднородных уравнений с двумя неизвестными

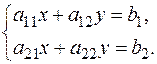
Обозначим

основной определитель системы;

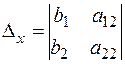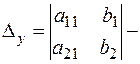, вспомогательные определители.

а) Если определитель системы 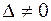, то система имеет единственное решение, которое находится по формулам Крамера:

, . (1)

б) Если определитель системы , то возможны случаи:

1) 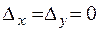(уравнения пропорциональны), тогда система содержит только одно уравнение, например, и имеет бесконечно много решений (неопределённая система). Для её решения необходимо выразить одну переменную через другую, значение которой выбирается произвольно;

2) если хотя бы один из определителей отличен от нуля, то система не имеет решений (несовместная система).

II) Система двух линейных однородных уравнений с тремя переменными

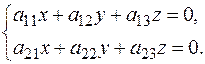(2)

Линейное уравнение называется однородным, если свободный член этого уравнения равен нулю.

а) Если , то система (2) сводится к одному уравнению (например, первому), из которого одно неизвестное выражается через два других, значения которых выбираются произвольно.

б) Если условие не выполнено, то для решения системы (2) перенесем одну переменную вправо и решим систему двух линейных неоднородных уравнений с использованием формул Крамера (1).

III) Система трёх линейных неоднородных уравнений с тремя неизвестными:

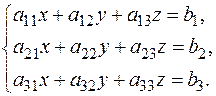
Составим и вычислим основной определитель и вспомогательные определители , .

а) Если 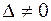, то система имеет единственное решение, которое находится по формулам Крамера:

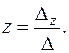, , (3)

б) Если , то возможны случаи:

1) 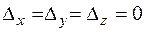, тогда система будет иметь бесконечно много решений, она будет сводиться либо к системе состоящей из одного, либо из двух уравнений (одну неизвестную перенесём направо и решим систему двух уравнений с двумя неизвестными);

2) хотя бы один из определителей 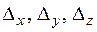отличен от нуля, система не имеет решения.

IV) Система трёх линейных однородных уравнений с тремя неизвестными:

Эта система всегда совместна, так как имеет нулевое решение.

а) Если определитель системы 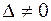, то она имеет единственное нулевое решение.

б) Если же , то система сводится либо к двум уравнениям (третье является их следствием), либо к одному уравнению (остальные два являются его следствием) и имеет бесконечно много решений (см. п. II).

Задача 4. Решить систему уравнений

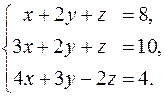
Решение. Вычислим определитель системы

Так как 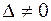, то система имеет единственное решение. Воспользуемся формулами Крамера (3). Для этого вычислим вспомогательные определители:

, ,

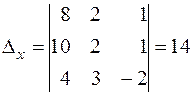Тогда

, ,

Задача 5. Решить систему уравнений

Решение. Вычислим определитель системы:

Следовательно, система однородных уравнений имеет бесконечно много решение, отличных от нулевого. Решаем систему первых двух уравнений (третье уравнение является их следствием):

Перенесём переменную 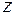в правую часть равенства:

Отсюда по формулам (1) получаем

, .

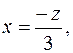
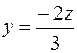Дата добавления: 2015-07-13