Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы

Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).

Совершенная дизъюнктивная нормальная форма (СДНФ) — это ДНФ, в которой в каждый конъюнктивный одночлен каждая переменная x_iиз набора f (x₁,x₂,..., х_п ) входит ровно один раз, причем входит либо сама х _i, либо ее отрицание Øх_i.

Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, можно определить так:

Алгоритм приведение булевых функций к Нормальным Формам при помощи таблиц истинности

Чтобы получить совершенную дизъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 1 и записать для каждого из них конъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять с отрицанием, если 1 – без отрицания. Из получившихся конъюнкций надо построить дизъюнкцию.

Чтобы получить совершенную конъюнктивную нормальную форму, надо взять все наборы, на которых значение функции равно 0 и записать для каждого из них дизъюнкцию переменных и их отрицаний. Если в наборе значение переменной 0 – то переменную надо взять без отрицания, если 1 – с отрицанием. Из получившихся дизъюнкций надо построить конъюнкцию.

Пример 3 (совершенная дизъюнктивная нормальная форма).

Построим совершенную дизъюнктивную нормальную форму функции, заданной следующей таблицей.

x	y	z	f

Наборы, на которых функция равна 1 – это (0,1,1), (1,0,1), (1,1,0), (1,1,1). Первый набор даёт конъюнкцию x & y & z, второй – x & y & z, третий – x & y & z, четвёртый – x & y & z. В результате получаем (x & y & z) ٧ (x & y & z) ٧ (x & y & z) v (x & y & z).

2. Пример выполнения:

1. Доказать с помощью таблиц истинности эквивалентность функций:

f(x,y,z)=x & (x٧z) & (y٧z) и f(x,y,z)=(x & y) ٧(х & z).

Решение:

Для доказательства необходимо построить таблицы истинности этих функций, и если их двоичные наборы совпадут, то эквивалентность будет доказана.

x	y	z	x٧z	y ٧z	x & (x٧z)	x & (x٧z) & (y٧z)

x	y	z	x٨ y	x ٨z	(x٨ y) ٧(x٨z)

Функции эквивалентны, так как их двоичные наборы совпадают.

2. Составить СДНФ для функции (X٨Y) ® (Y٨Z)

Решение: составим для заданной функции таблицу истинности и воспользуемся алгоритмом приведение булевых функций к Нормальным формам при помощи таблиц истинности.

X	Y	Z	(X٨Y)	(Y٨Z)	(X٨Y) ® (Y٨Z)

СДНФ для функции (X٨Y) ® (Y٨Z) будет иметь вид:

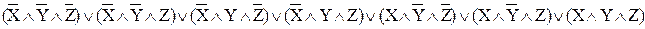
Дата добавления: 2015-07-13