
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Сумовні функції та простір Лебега
|
|
|
|
В цьому параграфі ми завершимо побудову інтегралу, продовживши його з класу  на деякий більш ширший клас
на деякий більш ширший клас  , в якому вже можна буде проводити всі звичні для функцій операції.
, в якому вже можна буде проводити всі звичні для функцій операції.
Сумовною (або інтегровною за Лебегом) функцією будемо називати довільну функцію 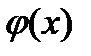
 яка може бути представлена як різниця
яка може бути представлена як різниця  двох функцій із класу
двох функцій із класу  .
.
Сукупність всіх сумовних функцій позначимо через  В класі сумовних функцій можна проводити наступні операції:
В класі сумовних функцій можна проводити наступні операції:
а) додавання.
Якщо 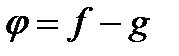 i
i 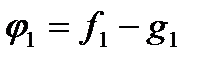 сумовні функції;
сумовні функції; 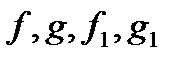 - функцій класу
- функцій класу  , то
, то 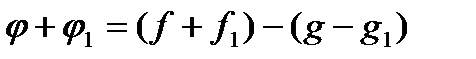 ,І так як
,І так як  ,
, 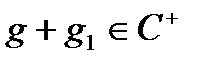 то
то 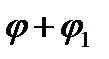 є функцією класу
є функцією класу  .
.
б) множення на будь-яке дійсне число 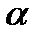 .
.
Якщо  ; то із
; то із 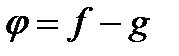 ,
, 
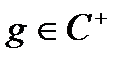 випливає, що
випливає, що 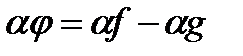 ,
,  ,
, 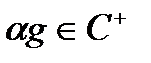 ,і, відповідно,
,і, відповідно,  ;
;
Якщо 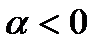 , то
, то  і рівність.
і рівність. 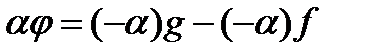 показує, що
показує, що 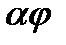 знову належать класу
знову належать класу  .
.
Із а) і б) випливає, що будь-які лінійні комбінації функцій класу  є також функціями класу
є також функціями класу  .
.
в) Взяття модуля функції.
Нехай 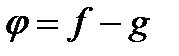 ,
,  ,
, 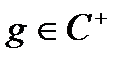 , тоді
, тоді  i
i 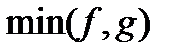 також належать класу
також належать класу 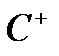 ; звідси
; звідси 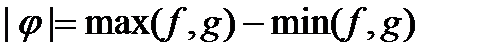 , належать класу
, належать класу  . Розв’язуючи рівняння
. Розв’язуючи рівняння 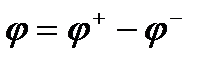 ,
,  .
.
Ми бачимо, що функції 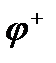 i
i  також належать класу
також належать класу  разом з функцією
разом з функцією 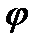 .
.
Далі рівності 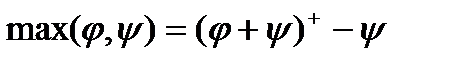 ,
,  показують, що разом з функціями
показують, що разом з функціями  i
i  в клас
в клас  входять їх максимум та мінімум.
входять їх максимум та мінімум.
Введемо тепер в клас  означення інтегралу. Для цього, маючи розклад
означення інтегралу. Для цього, маючи розклад 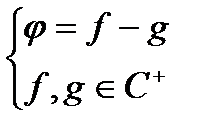 (1)
(1)
покладемо
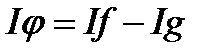
При цьому  визначається єдиним способом. Справді, нехай поряд з розкладом (1) ми маємо і інший розклад
визначається єдиним способом. Справді, нехай поряд з розкладом (1) ми маємо і інший розклад 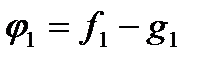 ,
, 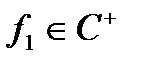 ,
, 
Доведемо, що  . Ця рівність еквівалентна рівності
. Ця рівність еквівалентна рівності 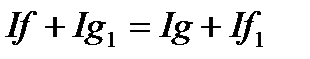 (*). Оскільки
(*). Оскільки 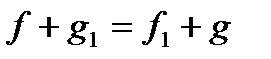 , то в силу єдиності інтеграла в класі
, то в силу єдиності інтеграла в класі  ми маємо:
ми маємо: 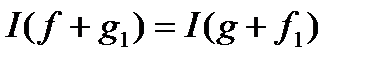 , звідки і випливає (*).
, звідки і випливає (*).
Надалі покажемо, що отриманий інтеграл володіє в класі  звичайними лінійними властивостями.
звичайними лінійними властивостями.
Нехай 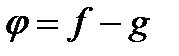 ,
, 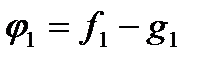 де
де 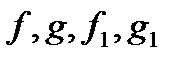 належить класу
належить класу 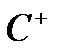 . Тоді
. Тоді 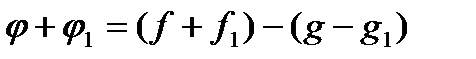 , і, згідно з означенням,
, і, згідно з означенням, 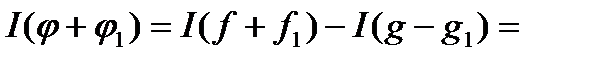
 .
.
Таким чином, інтеграл суми дорівнює сумі інтегралів. Далі, при 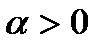
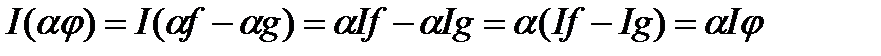 ; з іншого боку,
; з іншого боку, 
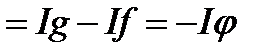 і, отже, при
і, отже, при 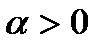 ми маємо
ми маємо 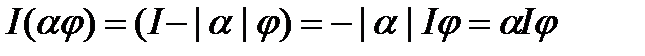 ; цим самим ми,фактично, довели, що число
; цим самим ми,фактично, довели, що число 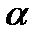 можна виносити за знак інтегралу. При будь-якому знаку
можна виносити за знак інтегралу. При будь-якому знаку  .
.
|
|
|
Зазначимо, що якщо  ,
,  , то
, то 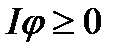 . Справді, якщо
. Справді, якщо 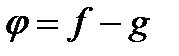 ,
,  ,
, 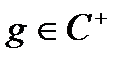 i
i  , то
, то  та
та  , тому
, тому  .Звідси отримаємо, що із
.Звідси отримаємо, що із  випливає
випливає  . Тепер доведемо важливу теорему про почленне інтегрування рядів з додатними доданками.
. Тепер доведемо важливу теорему про почленне інтегрування рядів з додатними доданками.
Теорема 3.1. (Беппо Леві, 1906). Якщо для ряду  ,
,  ,
, 
Інтеграли від частинних сум обмежені тобто 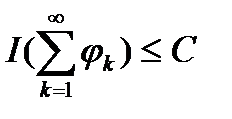 , то
, то  є сумовною функцією, і
є сумовною функцією, і  .
.
Доведення. Спершу зазначимо, що в розкладі сумовної функції 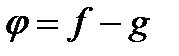 ,
,  ,
, 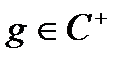 , функції
, функції 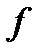 i
i  можна підпорядковувати подальшим умовам. Наприклад,
можна підпорядковувати подальшим умовам. Наприклад,  можна вибрати завжди так, щоб мати
можна вибрати завжди так, щоб мати 
 ,
,  задане число як завгодно мале. Для цього потрібно розглянути послідовність східчастих функцій
задане число як завгодно мале. Для цього потрібно розглянути послідовність східчастих функцій 
 так, що
так, що  і потім написати
і потім написати 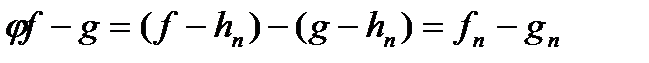 .
.
Очевидно, що при достатньо великому 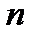 , умова, яка вимагається для функції
, умова, яка вимагається для функції 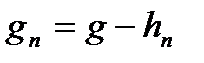 виконується. Замітимо при цьому, що якщо
виконується. Замітимо при цьому, що якщо 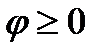 то і функція
то і функція 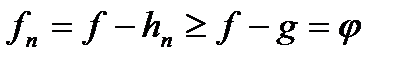 також отримується невід’ємною. Тепер для кожної із функцій
також отримується невід’ємною. Тепер для кожної із функцій 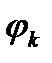 які беруть участь у формулюванні теореми, побудуємо розклад
які беруть участь у формулюванні теореми, побудуємо розклад 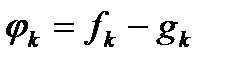 , де
, де 
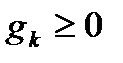 ,
, 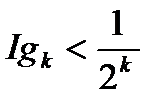 (
( При цьому ряд
При цьому ряд  задовольняє умови наслідку із теореми §2 (
задовольняє умови наслідку із теореми §2 (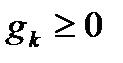 ,
,  . Тому
. Тому  належить до класу
належить до класу  та
та 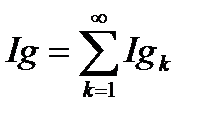 . Покажемо, що і ряд
. Покажемо, що і ряд  також задовольняє умови цього наслідку; дійсно, ми маємо
також задовольняє умови цього наслідку; дійсно, ми маємо  і
і  . Тому і
. Тому і 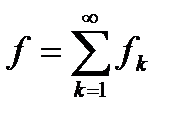 належить класу
належить класу  і
і 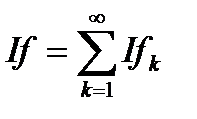 . Звідси
. Звідси  належить класу L
належить класу L 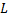 та
та 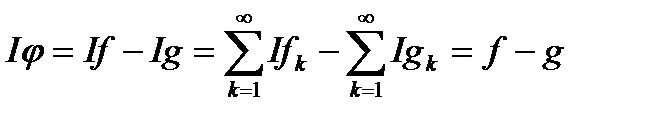 .
.
Цим самим ми довели нашу теорему 3.1.
Наслідок. Якщо сумовні функції 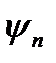 , монотонно зростаючи, прямують до
, монотонно зростаючи, прямують до 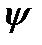 та
та 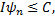
 то
то 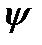 сумовна функція і
сумовна функція і  .
. 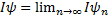
Для доведення досить покласти  і застосувати теорему 3. Аналогічний результат справедливий, зрозуміло, і для спадних послідовностей
і застосувати теорему 3. Аналогічний результат справедливий, зрозуміло, і для спадних послідовностей 
 , якщо тільки
, якщо тільки 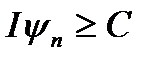 .
.
Надалі ми будемо розглядати довільні (немонотонні) граничні переходи. Класичні приклади показують, що не можна очікувати теореми вигляду “ із того, що 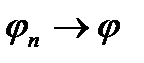 випливає
випливає 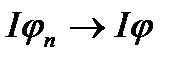 ” без додатних припущень про характер збіжності послідовності
” без додатних припущень про характер збіжності послідовності  до свої границі. Наприклад, функції
до свої границі. Наприклад, функції 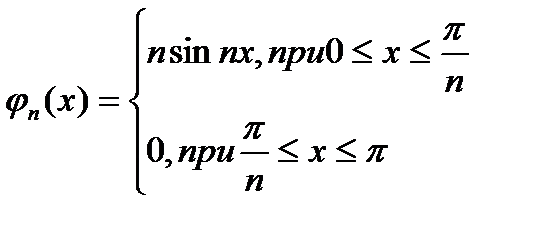 збігаються до нуля при будь-якому
збігаються до нуля при будь-якому  , в той час як інтеграли від них залишаються сталими (рівними 2) і не прямують до інтегралу від граничної функції.
, в той час як інтеграли від них залишаються сталими (рівними 2) і не прямують до інтегралу від граничної функції.
Розглянемо сукупність L 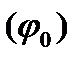 всіх сумовних функцій
всіх сумовних функцій  , які задовольняють нерівність
, які задовольняють нерівність
|
|
|
 ,
,
де  - фіксована невід’ємна сумовна функція. Очевидно, що для будь-якої функції
- фіксована невід’ємна сумовна функція. Очевидно, що для будь-якої функції 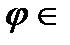 L
L 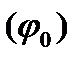 виконується нерівність
виконується нерівність 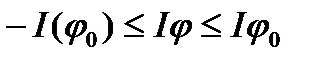 .
.
Якщо є монотонна послідовність функцій 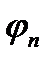 - спадна або зростаюча, - які належать сукупності L
- спадна або зростаюча, - які належать сукупності L 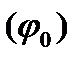 , то гранична функція
, то гранична функція  , зрозуміло, задовольняє нерівність разом з функціями
, зрозуміло, задовольняє нерівність разом з функціями 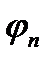 ; ця функція, згідно наслідку 2, є сумовною. Отже, сукупність L
; ця функція, згідно наслідку 2, є сумовною. Отже, сукупність L 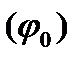
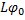 замкнена відносно монотонних граничних переходів.
замкнена відносно монотонних граничних переходів.
Замітимо, що для будь-якої послідовності  L
L 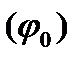 можна стверджувати, що функції
можна стверджувати, що функції  та
та 
Також належать сукупності L 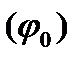 : перша з них являється границею при
: перша з них являється границею при 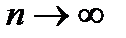 зростаючої послідовності функцій
зростаючої послідовності функцій  L
L 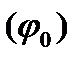 , а інша – границею спадною послідовності функцій
, а інша – границею спадною послідовності функцій  L
L 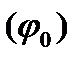 .
.
Нехай тепер  L
L 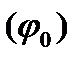 довільна послідовність, яка збігається майже скрізь до деякої функції
довільна послідовність, яка збігається майже скрізь до деякої функції  ; покажемо, що
; покажемо, що  також належить класу L
також належить класу L 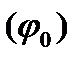 . Досить показати, що
. Досить показати, що  представлена у вигляді границі деякої монотонної послідовності функцій із класу L
представлена у вигляді границі деякої монотонної послідовності функцій із класу L 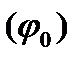 . Покладемо
. Покладемо
 ,
,
 .
.
За доведеним, ці функції сумовні і належать класу L 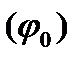 . Якщо розглянути тільки ті значення
. Якщо розглянути тільки ті значення  , де функції
, де функції  мають границю
мають границю  , то oчевидно, що при будь-якому такому значенні
, то oчевидно, що при будь-якому такому значенні  ,
, 
Отже,  спадаюча а
спадаюча а  зростаюча послідовності. Далі, зрозуміло, що із того, що
зростаюча послідовності. Далі, зрозуміло, що із того, що  випливає, що
випливає, що 
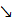
 i
i  Таким чином функція
Таким чином функція  виявляється границею зростаючої послідовності функцій класу L
виявляється границею зростаючої послідовності функцій класу L 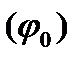 (і одночасно границею спадної послідовності цього класу). Звідси
(і одночасно границею спадної послідовності цього класу). Звідси  L
L 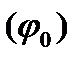 , що й стверджувалось. При цьому ми маємо, що
, що й стверджувалось. При цьому ми маємо, що 
 ,
, 
 i
i 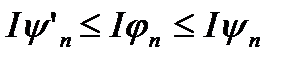 звідки
звідки  .
.
Цим самим ми довели наступну теорему:
Теорема 3.2. (Лебег, 1902). Якщо послідовність сумовних функцій 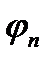 збіжна майже скрізь до функції
збіжна майже скрізь до функції 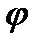 і задовольняє умову:
і задовольняє умову: 
 то
то 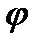 сумовна функція та
сумовна функція та 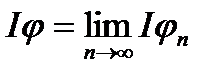
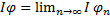 .
.
Взагалі кажучи, рівність 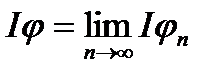 справедлива, якщо функції
справедлива, якщо функції 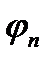 обмежені в сукупності.
обмежені в сукупності.
З цієї теореми ми можемо отримати важливий результат відносно складу класу L 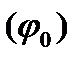 .
.
Теорема 3.3. Якщо деяка вимірна функція 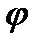 задовольняє (майже скрізь) нерівність
задовольняє (майже скрізь) нерівність 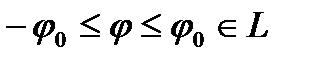 , то вона сумовна (і цим самим належить до класу
, то вона сумовна (і цим самим належить до класу 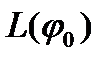
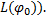 ).
).
Доведення. Нехай 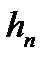 послідовність східчастих функцій, яка визначає вимірну функцію
послідовність східчастих функцій, яка визначає вимірну функцію 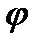 . Обрізуючи її зверху по рівню
. Обрізуючи її зверху по рівню 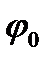 і знизу по рівню
і знизу по рівню 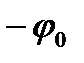 , тобто замінюючи її функцією
, тобто замінюючи її функцією 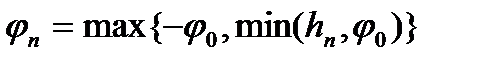 ми отримаєм послідовність сумовних функцій, які належать класу
ми отримаєм послідовність сумовних функцій, які належать класу 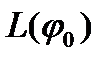 , збіжну майже скрізь до функції
, збіжну майже скрізь до функції 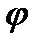 . Отже,
. Отже,  є сумовною функцією, що і вимагалось.
є сумовною функцією, що і вимагалось.
Взагалі кажучи, довільна обмежена вимірна функція сумовна.
|
|
|
З іншого боку, доведена нами теорема про сумовні функції дозволяє зробити подальші зауваження про вимірні функції. Покажемо, що границя  збіжної майже скрізь послідовності вимірних функцій
збіжної майже скрізь послідовності вимірних функцій 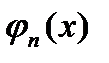 якщо вона скінченна майже скрізь – є вимірною функцією. Достатньо розглянути випадок
якщо вона скінченна майже скрізь – є вимірною функцією. Достатньо розглянути випадок  , оскільки в противному випадку можна окремо розглянути послідовності
, оскільки в противному випадку можна окремо розглянути послідовності  i
i  . Але, якщо майже скрізь
. Але, якщо майже скрізь 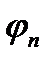 збігається до
збігається до 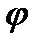 , то також майже скрізь послідовність функцій
, то також майже скрізь послідовність функцій  збігається до
збігається до 
 .
.
Функції  знаходяться між нулем і одиницею і вимірні. Тому вони сумовні, а їх границя
знаходяться між нулем і одиницею і вимірні. Тому вони сумовні, а їх границя 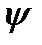 доведеним, - також сумовна і, отже, вимірна функція.
доведеним, - також сумовна і, отже, вимірна функція.
Зауважимо, що 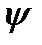 може приймати значення нуль тільки там, де
може приймати значення нуль тільки там, де 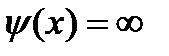 тобто на множині міри нуль. Тому, перетворюючи отриману рівність, знайдемо, що і
тобто на множині міри нуль. Тому, перетворюючи отриману рівність, знайдемо, що і  є вимірною функцією, оскільки чисельник і знаменник отриманого відношення вимірні і знаменник майже скрізь відмінний від нуля.
є вимірною функцією, оскільки чисельник і знаменник отриманого відношення вимірні і знаменник майже скрізь відмінний від нуля.
В одному випадку можна стверджувати сумовність граничної функції послідовності  , замінивши припущення про обмеженості функцій
, замінивши припущення про обмеженості функцій  сумовної функції деяким іншим припущеннями:
сумовної функції деяким іншим припущеннями:
Лема. Фату (1906). Якщо  - сумовні функції,
- сумовні функції,  майже скрізь і
майже скрізь і  ,
,  сумовна функція і
сумовна функція і 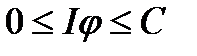 .
.
Доведення. Покладемо 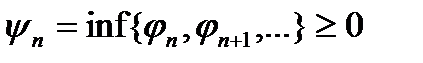 . Так як і вище, функції
. Так як і вище, функції 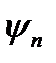 утворюють зростаючу послідовність, збіжну майже скрізь до функції
утворюють зростаючу послідовність, збіжну майже скрізь до функції 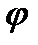 . Далі,
. Далі, 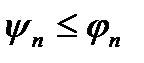 ,
,  ; в силу теореми Беппо Леві функція
; в силу теореми Беппо Леві функція 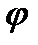 - сумовна і
- сумовна і 
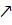
 Взагалі кажучи,
Взагалі кажучи,  що і потрібно було довести.
що і потрібно було довести.
Нехай функція 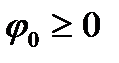 сумовна та
сумовна та 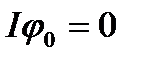 ; покажемо, що
; покажемо, що  майже скрізь. Покажемо що
майже скрізь. Покажемо що 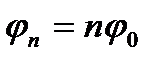 ; функція
; функція  прямує до границі
прямує до границі 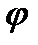 , рівний нулеві там, де
, рівний нулеві там, де 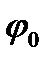 рівна нулеві і безмежності там, де
рівна нулеві і безмежності там, де  . Але, так, як, за лемою Фату, гранична функція повинна бути сумовною, взагалі кажучи, вимірною, то множина тих
. Але, так, як, за лемою Фату, гранична функція повинна бути сумовною, взагалі кажучи, вимірною, то множина тих 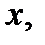 де
де  є множиною міри нуль. Разом з тим і множина тих
є множиною міри нуль. Разом з тим і множина тих 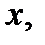
 , є множиною міри нуль. Ми отримаємо:
, є множиною міри нуль. Ми отримаємо:
якщо 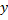 невід’ємної сумовної функції
невід’ємної сумовної функції  інтеграл рівний нулеві, то ця функція
інтеграл рівний нулеві, то ця функція 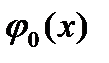 сама майже скрізь рівна нулеві.
сама майже скрізь рівна нулеві.
Перейдемо до класів еквівалентних функцій: дві функції вважаються еквівалентними, якщо вони збігаються на множині повної міри. Зокрема, що найбільше на множині міри нуль. Функції, еквівалентні нулю, відображають, очевидно, підпростір  в лінійний простір L всіх сумовних функцій.
в лінійний простір L всіх сумовних функцій.
|
|
|
У просторі L введемо переднорму
 (1)
(1)
Справді, число 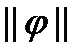 невід’ємне, причому рівне нулеві тільки для функції, майже скрізь рівній нулеві, далі мають місце співвідношення:
невід’ємне, причому рівне нулеві тільки для функції, майже скрізь рівній нулеві, далі мають місце співвідношення:
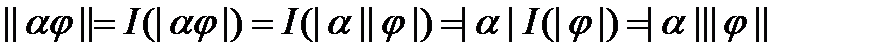
 ,
,
Підпростір  складається із тих і тільки тих функцій, які переднорма рівна нулю. І тому в класів еквівалентних сумовних функцій можна ввести норму, яка рівна
складається із тих і тільки тих функцій, які переднорма рівна нулю. І тому в класів еквівалентних сумовних функцій можна ввести норму, яка рівна  , де
, де 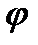 довільна функція із цього класу. Отже, ми отримаєм лінійний нормований простір, класів еквівалентних сумовних функцій, який будем називати простором Лебега.
довільна функція із цього класу. Отже, ми отримаєм лінійний нормований простір, класів еквівалентних сумовних функцій, який будем називати простором Лебега.
Теорема 3.4. (Е.Фішер, Ф. Рір, 1907). Простір Лебега – є баноховим простором.
Перш ніж переходити до доведення цього твердження, зауважимо що: по-перше, елементи будь-якої фундаментальної послідовності обмежені за нормою, оскільки, починаючи з деякого номера, всі ці елементи містяться в кулі радіуса 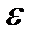 з центром в деякій точці
з центром в деякій точці  ; по-друге, для доведення існування границі фундаментальної послідовності
; по-друге, для доведення існування границі фундаментальної послідовності  достатньо показати, що існує границя
достатньо показати, що існує границя  деякої послідовності
деякої послідовності 
 ; цей елемент
; цей елемент  буде границею і всієї послідовності
буде границею і всієї послідовності  в силу нерівності
в силу нерівності 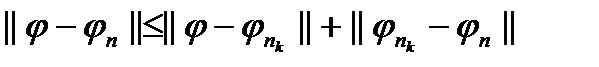 причому другий доданок справа прямує до нуля в силу фундаментальної послідовності
причому другий доданок справа прямує до нуля в силу фундаментальної послідовності  .
.
Тепер перейдемо до доведення теореми.
Доведення. Нехай  фундаментальна послідовність у просторі L. Завжди можна вибрати послідовність індексів
фундаментальна послідовність у просторі L. Завжди можна вибрати послідовність індексів  так, щоб при
так, щоб при 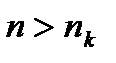 виконувались нерівності:
виконувались нерівності:  (k=1,2,…,). Взагалі кажучи,
(k=1,2,…,). Взагалі кажучи, 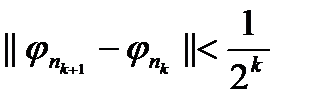 ; це означає, що
; це означає, що 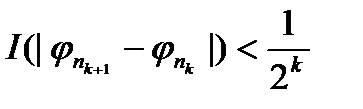 .
.
Але тоді ряд сумовних функцій 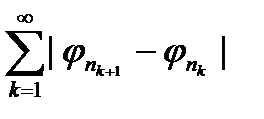 згідно з теореми Беппо Леві, збігається майже скрізь. Звідси слідує, що збігається майже скрізь і ряд з частинними сумами
згідно з теореми Беппо Леві, збігається майже скрізь. Звідси слідує, що збігається майже скрізь і ряд з частинними сумами  . Це означає існування границі майже скрізь при
. Це означає існування границі майже скрізь при 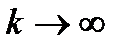 у функції
у функції  . Позначимо цю границю через
. Позначимо цю границю через 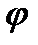 . Функція
. Функція 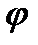 вимірна як границя вимірних функцій. Так як норми функцій
вимірна як границя вимірних функцій. Так як норми функцій  , тобто числа
, тобто числа 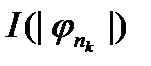 обмежені, то, за лемою Фату, функція
обмежені, то, за лемою Фату, функція  сумовна. Отже, сумовна і вимірна функція
сумовна. Отже, сумовна і вимірна функція 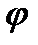 . Далі, за тією ж лемою, застосованої до функції
. Далі, за тією ж лемою, застосованої до функції 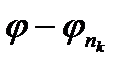 , ми маємо:
, ми маємо: 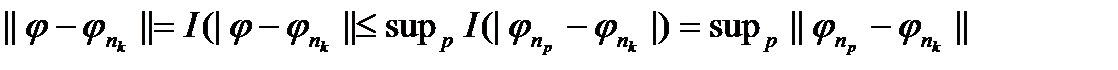
Але останній інтеграл за умовою може бути, при достатньо великому 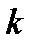 , як завгодно малим. Отже,
, як завгодно малим. Отже,  збігається до
збігається до  за нормою простору L, і теорему доведено.
за нормою простору L, і теорему доведено.
На завершення покажемо, що простір L є поповненням простору 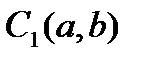 неперервних функцій
неперервних функцій  на відрізку
на відрізку  з метрикою:
з метрикою: 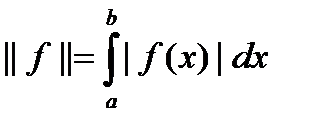
Простір  містить простір
містить простір 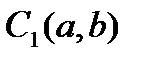 як підпростір з тією ж метрикою. Тому нам достатньо показати, що
як підпростір з тією ж метрикою. Тому нам достатньо показати, що 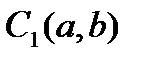 міститься в L як щільна підмножина, так що кожну функцію
міститься в L як щільна підмножина, так що кожну функцію 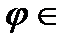 L можна представити як границю послідовності функцій
L можна представити як границю послідовності функцій  . Легко переконатися, що кожна східчаста функція
. Легко переконатися, що кожна східчаста функція  володіє цією властивістю. З іншого боку, оскільки кожна функція
володіє цією властивістю. З іншого боку, оскільки кожна функція  L є різницею двох функцій із класу
L є різницею двох функцій із класу  , досить перевірити наше твердження для функцій із класу
, досить перевірити наше твердження для функцій із класу  . Нехай
. Нехай 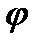 належить
належить  і
і 
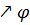 послідовність східчастих функцій. Тоді
послідовність східчастих функцій. Тоді  і так як
і так як 
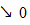 то за теоремою Беппо Леві
то за теоремою Беппо Леві 
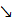
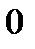 ,
,
що і потрібно було встановити.
Література
1. Г.Е.Шилов, Математический анализ, Специальный курс; Физматгиз 1961, с.137-158.
2. Лекції з функціонального аналізу: Ч.1. метричні і нормовані простори: навч. посібник./ укл.: В.К.Маслюченко. - Чернівці: Чернівецький нац. ун-т, 2010.-184с.
3. Лекції з теорії міри та інтеграла: Ч.1. Міра: навч. посібник./ В.К.Маслюченко.-Чернівці: Чернівецький нац. ун-т, 2011.-156с.
4. Лекції з теорії міри та інтеграла: Ч.2. Інтеграл: навч. посібник./ В.К.Маслюченко.-Чернівці: Чернівецький нац. ун-т, 2011.-176с.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 1775; Нарушение авторских прав?; Мы поможем в написании вашей работы!