Потенциал

Теорема о циркуляции для электростатического поля.

Поскольку электростатическое поле является центральным, то силы, действующие на заряд в таком поле, являются консервативными. Так как 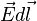представляет собой элементарную работу, которую силы поля производят над единичным зарядом, то работа консервативных сил на замкнутом контуре равна

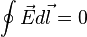
Из механики известно, что работа консервативных сил связана с изменением потенциальной энергии. Система "заряд — электростатическое поле" обладает потенциальной энергией (энергией электростатического взаимодействия). Поэтому, если не учитывать взаимодействие заряда с гравитационным полем и окружающей средой, то работа, совершаемая при перемещении заряда в электростатическом поле, равна изменению потенциальной энергии заряда, взятому с противоположным знаком:

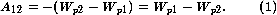
Если W_p2 = 0, то в каждой точке электростатического поля потенциальная энергия заряда q₀ равна работе, которая была бы совершена при перемещении заряда q₀ из данной точки в точку с нулевой энергией.

Пусть электростатическое поле создано в некоторой области пространства положительным зарядом q (рис. 1).

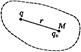
Рис. 1

Будем помещать в точку М этого поля различные пробные положительные заряды q₀. Потенциальная энергия их различна, но отношение 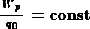для данной точки поля и служит характеристикой поля, называемой потенциалом поля 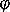в данной точке:

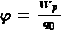
Единицей потенциала в СИ является вольт (В) или джоуль на кулон (Дж/Кл).

Потенциалом электростатического поля в данной точке называют скалярную физическую величину, характеризующую энергетическое состояние поля в данной точке пространства и численно равную отношению потенциальной энергии, которой обладает пробный положительный заряд, помещенный в эту точку, к значению заряда.

Потенциал — это энергетическая характеристика поля в отличие от напряженности поля, являющейся силовой характеристикой поля.

Необходимо отметить, что потенциальная энергия заряда в данной точке поля, а значит, и потенциал зависят от выбора нулевой точки. Нулевой эта точка называется потому, что потенциальную энергию (соответственно потенциал) заряда, помещенного в эту точку поля, уславливаются считать равной нулю.

Нулевой уровень потенциальной энергии выбирается произвольно, поэтому потенциал можно определить только с точностью до некоторой постоянной, значение которой зависит от того, в какой точке пространства выбрано его нулевое значение.

В технике принято считать нулевой точкой любую заземленную точку, т.е. соединенную проводником с землей. В физике за начало отсчета потенциальной энергии (и потенциала) принимается любая точка, бесконечно удаленная от зарядов, создающих поле. Если нулевая точка выбрана, то потенциальная энергия (соответственно и потенциал в данной точке) заряда q₀ становится определенной величиной.

На расстоянии r от точечного заряда q, создающего поле, потенциал определяется формулой

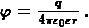
При указанном выше выборе нулевой точки потенциал в любой точке поля, создаваемого положительным зарядом q, положителен, а поля, создаваемого отрицательным зарядом, отрицателен:

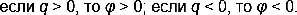
По этой формуле можно рассчитывать потенциал поля, образованного равномерно заряженной проводящей сферой радиусом R в точках, находящихся на поверхности сферы и вне ее. Внутри сферы потенциал такой же, как и на поверхности, т.е.

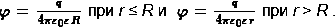
Если электростатическое поле создается системой зарядов, то имеет место принцип суперпозиции: потенциал в любой точке такого поля равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

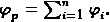
Зная потенциал 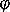поля в данной точке, можно рассчитать потенциальную энергию заряда q0 помещенного в эту точку: W_p1 = q₀ 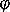. Если положить, что W_p2 = 0, то из уравнения (1) будем иметь

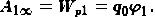
Потенциальная энергия заряда q₀ в данной точке поля будет равна работе сил электростатического поля по перемещению заряда q0 из данной точки в нулевую. Из последней формулы имеем

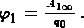
Потенциал поля в данной точке численно равен работе по перемещению единичного положительного заряда из данной точки в нулевую (в бесконечность).

Потенциальная энергия заряда q₀ помещенного в электростатическое поле точечного заряда q на расстоянии r от него,

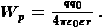
Если q и q₀ — одноименные заряды, то 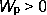, если q и q₀ — разные по знаку заряды, то .

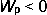Отметим еще раз, что по этой формуле можно рассчитать потенциальную энергию взаимодействия двух точечных зарядов, если за нулевое значение W_p выбрано ее значение при r = бесконечности.

Если электростатическое поле образовано системой n точечных электрических зарядов, то потенциальная энергия системы определяется по формуле

где 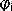— потенциал поля, созданного всеми зарядами, кроме заряда q_i, в той точке поля, где находится заряд q_i.

Уравне́ние Пуассо́на — эллиптическое дифференциальное уравнение в частных производных, которое описывает

электростатическое поле,

стационарное поле температуры,

поле давления,

поле потенциала скорости в гидродинамике.

Оно названо в честь знаменитого французского физика и математика Симеона Дени Пуассона.

Это уравнение имеет вид: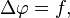

где 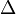— оператор Лапласа, или лапласиан, а — вещественная или комплексная функция на некотором многообразии.

В трёхмерной декартовой системе координат уравнение принимает форму:

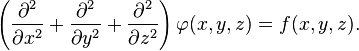
В декартовой системе координат оператор Лапласа записывается в форме 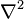и уравнение Пуассона принимает вид:

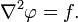
Если f стремится к нулю, то уравнение Пуассона превращается в уравнение Лапласа (уравнение Лапласа — частный случай уравнения Пуассона):

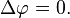
Уравнение Пуассона может быть решено с использованием функции Грина; см., например, статью экранированное уравнение Пуассона. Есть различные методы для получения численных решений. Например, используется итерационный алгоритм — «релаксационный метод».

Уравнение Пуассона является одним из важнейших уравнений электростатики. Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:

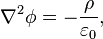
где — электростатический потенциал (в вольтах), 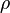— объёмная плотность заряда (в кулонах на кубический метр), а 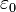— диэлектрическая проницаемость вакуума (вфарадах на метр).

В единицах системы СГС:

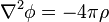
В области пространства, где нет непарной плотности заряда, имеем:

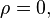
и уравнение для потенциала превращается в уравнение Лапласа:

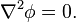
Уравнение Пуассона выводится из закона Гаусса и определения статического потенциала:

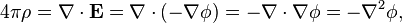
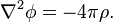
2. Волновая функция, ее смысл. Операторы координаты и импульса. Средние значения физических величин. Соотношение неопределенностей для координат и импульса. Уравнение Шредингера.

Волнова́я фу́нкция, или пси-функция 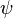— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

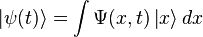
где 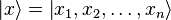— координатный базисный вектор, а 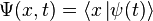— волновая функция в координатном представлении.

Согласно копенгагенской интерпретации квантовой механики плотность вероятности нахождения частицы в данной точкеконфигурационного пространства в данный момент времени считается равной квадрату абсолютного значения волновой функции этого состояния в координатном представлении. В координатном представлении волновая функция 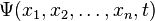зависит от координат (или обобщённых координат) системы. Сама волновая функция физического смысла не имеет, но физический смысл приписывается квадрату её модуля 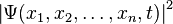, который интерпретируется как плотностьвероятности 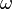(для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 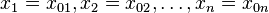в момент времени :

.

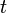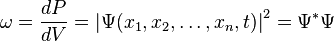Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 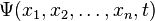, можно рассчитать вероятность 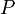того, что частица будет обнаружена в любой области конфигурационного пространства конечного объема : .

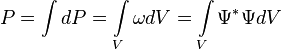
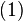Следует также отметить, что возможно измерение и разницы фаз волновой функции, например, в опыте Ааронова — Бома.

Дата добавления: 2015-08-31