
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Означення
|
|
|
|
Теорема.
Означення.
Теорема 2.
Теорема 1.
Існує така ортогональні стохастична міра 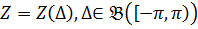 , що для кожного
, що для кожного  (
( 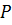 -м.н.)
-м.н.)
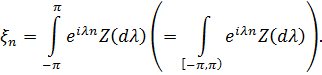
При цьому  .
.
Якщо 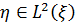 , то знайдеться така функція
, то знайдеться така функція 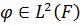 , що (
, що ( 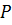 -м.н.)
-м.н.)
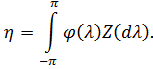
2.5 Регулярні послідовності
Введемо позначення. Нехай  та
та 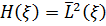 – замкнені лінійні многовиди, породжені величинами
– замкнені лінійні многовиди, породжені величинами 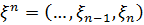 і
і  відповідно. Нехай також
відповідно. Нехай також
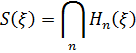
Стаціонарна послідовність 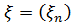 називається регулярною, якщо
називається регулярною, якщо

і сингулярною, якщо
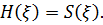
Кожна стаціонарна в широкому сенсі випадкова послідовність  допускає єдиний розклад
допускає єдиний розклад
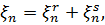
де 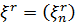 – регулярна, а
– регулярна, а 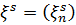 – сингулярна послідовності. При цьому
– сингулярна послідовності. При цьому 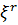 і
і  ортогональні (
ортогональні (  .
.
Клас Харді 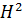 – це клас аналітичних функцій
– це клас аналітичних функцій 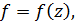 у відкритому одиничному колі
у відкритому одиничному колі 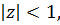 на комплексній площин, які задовольняють умову
на комплексній площин, які задовольняють умову

Теорема (Колмагоров).
Нехай  – не вироджена регулярна стаціонарна послідовність. Тоді існує спектральна щільність
– не вироджена регулярна стаціонарна послідовність. Тоді існує спектральна щільність 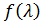 така, що
така, що

А саме,  (майже скрізь по мірі Лебега).
(майже скрізь по мірі Лебега).
І навпаки, якщо  – деяка стаціонарна послідовність, що має спектральну щільність, яка задовольняє умову (1), то ця послідовність є регулярною.
– деяка стаціонарна послідовність, що має спектральну щільність, яка задовольняє умову (1), то ця послідовність є регулярною.
2.6 Екстраполяція, інтерполяція та фільтрація
Екстраполяція.
Розглянемо частковий випадок, коли спектральна щільність задається у вигляді

де функція  має радіус збіжності
має радіус збіжності  і не має нулів в радіусі
і не має нулів в радіусі 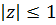
Нехай

– спектральне представлення послідовності 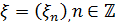 .
.
Теорема 1. Якщо спектральна щільність послідовності  може бути представлена у вигляді (1), то оптимальна (лінійна) оцінка
може бути представлена у вигляді (1), то оптимальна (лінійна) оцінка 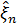 величини
величини  по
по 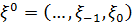 задається формулою
задається формулою

де
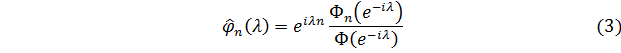
та
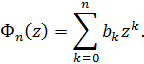
Інтерполяція.
Найпростішою задачею інтерполяції є задача побудови оптимальної (в середньоквадратичному сенсі) лінійної оцінки по результатамспостережень  «пропущеного» значення
«пропущеного» значення  .
.
Позначимо через  – замкнений лінійний многовид, породжений величинами
– замкнений лінійний многовид, породжений величинами 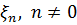 . Тоді кожна випадкова величина
. Тоді кожна випадкова величина 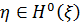 може бути представлена у вигляді
може бути представлена у вигляді
|
|
|
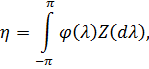
де  належить
належить 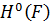 замкненому лінійному многовиду, породженому функціями
замкненому лінійному многовиду, породженому функціями  і оцінка
і оцінка

буде оптимальною тоді і тільки тоді, коли

Із властивостей «перпендикулярів» в гільбертовому просторі 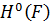 випливає, що функція
випливає, що функція 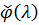 повністю визначається двома умовами:
повністю визначається двома умовами:
1) 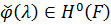
2) 
Теорема 2 (Колмагоров).
Нехай 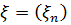 – регулярна послідовність з
– регулярна послідовність з
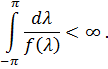
Тоді
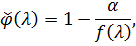
де
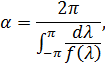
І похибка інтерполяції 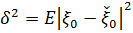 задається формулою
задається формулою 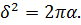
Фільтрація.
Задача фільтрації полягає в побудові оптимальної (в середньоквадратичному сенсі) лінійної оцінки 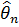 величини
величини  по тім чи іншим спостереженням послідовності
по тім чи іншим спостереженням послідовності 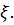
Оскільки 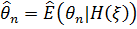 , то знайдеться така функція
, то знайдеться така функція 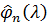 , що
, що

Оптимальна функція 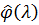 :
:
1) 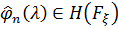 ,
,
2) 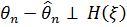 .
.
Отриманий розв’язок (4) можна використати для побудови оптимальної оцінки 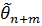 величини
величини 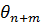 по результатам спостережень
по результатам спостережень 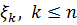 , де
, де  – деяке задане число з
– деяке задане число з 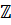 .
.
2.7 Двоїстість та ортогоналізація
Надалі ми припускаємо, що 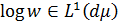 такий, що
такий, що 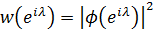 для деякої функції 𝜑 з класу Харді
для деякої функції 𝜑 з класу Харді 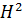 . Нехай
. Нехай 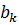 і
і 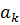 це коефіцієнти в наступних розкладах:
це коефіцієнти в наступних розкладах:

Зауважимо, що
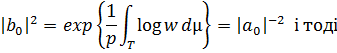

Явний вигляд для 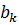 і
і 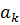 в термінах коефіцієнтів ряду Фур’є для
в термінах коефіцієнтів ряду Фур’є для  можна знайти в [11] та [12].
можна знайти в [11] та [12].
Для набору індексів 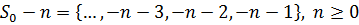 , котрі відповідають видаленню перших n частот з
, котрі відповідають видаленню перших n частот з  , відомо, що
, відомо, що

(див. [7], [11], [2]). Це так званий 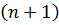 – й крок прогнозу дисперсії. Для множини індексів
– й крок прогнозу дисперсії. Для множини індексів 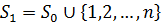 котрий дорівнює приєднанню наступних
котрий дорівнює приєднанню наступних 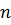 частот до
частот до  в [10] показано, що
в [10] показано, що
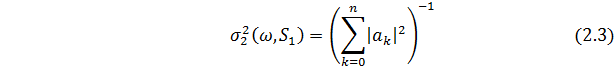
якщо 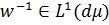 . Дуже цікавий обернений зв'язок між співвідношеннями (2.2) і (2.3), а також потреба в нетривіальній умові
. Дуже цікавий обернений зв'язок між співвідношеннями (2.2) і (2.3), а також потреба в нетривіальній умові 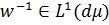 пояснюється встановленням двоїстості між
пояснюється встановленням двоїстості між 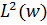 та
та 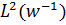 як Банахових просторів (див. [9], [2]). Відмітимо, що доповнення
як Банахових просторів (див. [9], [2]). Відмітимо, що доповнення 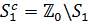 із
із 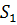 в
в  еквівалентно півосі
еквівалентно півосі 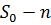 , де
, де 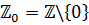 . Отже, загальна і більш складна проблема прогнозування на основі
. Отже, загальна і більш складна проблема прогнозування на основі 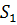 в
в 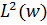 була зведена до звичайної проблеми прогнозування в
була зведена до звичайної проблеми прогнозування в 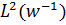 . В цілому, для будь-якого набору індексів
. В цілому, для будь-якого набору індексів 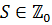 із скінченним числом точок із
із скінченним числом точок із 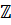 добавлених чи відібраних, нехай
добавлених чи відібраних, нехай 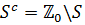 буде доповненням
буде доповненням 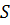 до
до 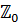 , і для фіксованого
, і для фіксованого 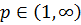 , визначимо
, визначимо 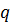 та
та  наступною рівністю:
наступною рівністю:
|
|
|
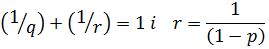
відповідно. Тоді той же аргумент двоїстості показує, що
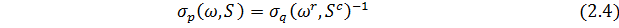
якщо 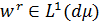 . Хоча останнє нетривіальне обмеження може бути послаблене [2], до
. Хоча останнє нетривіальне обмеження може бути послаблене [2], до  , але величина
, але величина  , можливо, не буде чітко визначена. На щастя, для набору
, можливо, не буде чітко визначена. На щастя, для набору 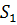 ця складність була усунута в [2, Теорема 3], використовуючи іншу задачу екстремальної двоїстості в [3], пов’язану з проекцією
ця складність була усунута в [2, Теорема 3], використовуючи іншу задачу екстремальної двоїстості в [3], пов’язану з проекцією  на простір Харді
на простір Харді 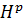 . Тим не менш, для загального
. Тим не менш, для загального 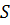 , визначення правої частини рівності (2.4) залишається відкритим питанням. В ідеалі хотілося б застосувати (2.4), коли одна проблема простіша, ніж інша, однак (2.4) не має сенсу, коли проблеми прогнозування, що відповідають
, визначення правої частини рівності (2.4) залишається відкритим питанням. В ідеалі хотілося б застосувати (2.4), коли одна проблема простіша, ніж інша, однак (2.4) не має сенсу, коли проблеми прогнозування, що відповідають 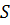 та
та 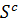 мають однакову складність або ж навіть ідентичні. У попередньому випадку, підходяща ортогоналізація у поєднанні з (2.4), здається, забезпечує гарний метод для розв’язку деяких проблем прогнозування. Наприклад, для
мають однакову складність або ж навіть ідентичні. У попередньому випадку, підходяща ортогоналізація у поєднанні з (2.4), здається, забезпечує гарний метод для розв’язку деяких проблем прогнозування. Наприклад, для  доповнення
доповнення 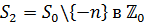 еквівалентно
еквівалентно  , що відповідає вилученню і приєднанню одного спостереження в
, що відповідає вилученню і приєднанню одного спостереження в  відповідно. Жодна з проблем не є тривіальною, але останнє здається простіше. В [2, теореми 5, 6] метод ортогоналізації використовується для обчислення
відповідно. Жодна з проблем не є тривіальною, але останнє здається простіше. В [2, теореми 5, 6] метод ортогоналізації використовується для обчислення 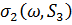 . Тоді співвідношення двоїстості (2.4) використовується для визначення
. Тоді співвідношення двоїстості (2.4) використовується для визначення 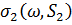 , що дає:
, що дає:

(2.5)
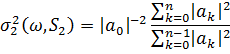
В цьому пункті ми обчислюємо  для більш загального набору індексів
для більш загального набору індексів  з
з  і
і 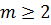 , тобто
, тобто
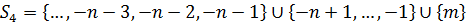
Цей набір індексів має властивості як  так і
так і 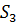 . Насправді, він зводиться до
. Насправді, він зводиться до  , коли
, коли 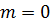 , в той час як його доповнення
, в той час як його доповнення 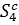 в
в 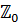 має той же вигляд, як і
має той же вигляд, як і  , так, що відношення двоїстості (2.4) не має сенсу. Тут також показано, що метод ортогоналізації, головним кроком якого є визначення проекції
, так, що відношення двоїстості (2.4) не має сенсу. Тут також показано, що метод ортогоналізації, головним кроком якого є визначення проекції  з
з  на підпростір
на підпростір 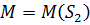 , може бути використаний для вирішення проблеми. Щоби встановити значення, позначимо ортогональну проекцію
, може бути використаний для вирішення проблеми. Щоби встановити значення, позначимо ортогональну проекцію  на підпростір
на підпростір  . Оскільки
. Оскільки  ортогональні до
ортогональні до 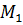 , то підпростори
, то підпростори 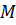 і
і 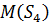 можна записати у вигляді наступних ортогональних сум:
можна записати у вигляді наступних ортогональних сум:
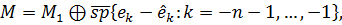
(2.6)
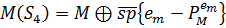
Таким чином, обчислення  , його проекції та норми являється першочерговим. Наступна тотожність, яка являє собою узагальнення [2, теорема 6], представляє окремий інтерес. Власне, цікавий її зв’язок з
, його проекції та норми являється першочерговим. Наступна тотожність, яка являє собою узагальнення [2, теорема 6], представляє окремий інтерес. Власне, цікавий її зв’язок з 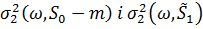 , де
, де 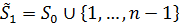 (з
(з 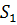 , де
, де  ):
):

 (2.7)
(2.7)
Де  i
i
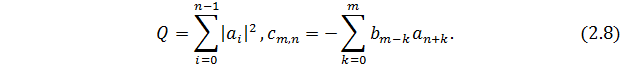
Константа 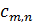 насправді являється коефіцієнтом
насправді являється коефіцієнтом 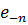 у формальному розкладі в ряд
у формальному розкладі в ряд 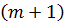 -го кроку прогнозу
-го кроку прогнозу  . [16]). Наостанок, бажана відстань:
. [16]). Наостанок, бажана відстань:
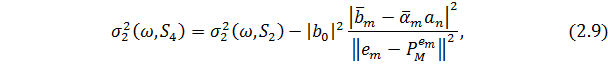
Де

На відміну від (2.2), (2.3) і (2.5), де відстань залежить або ж лише від 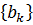 або лише від
або лише від 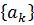 , у випадку (2.7) і (2.9) одночасно залежить від обох. Явні вирази цих відстаней забезпечують корисні інструменти для оцінки впливу додавання (вилучення) вектора на зниження (підвищення) таких відстаней. А саме, як слідує з (2.7), видалення
, у випадку (2.7) і (2.9) одночасно залежить від обох. Явні вирази цих відстаней забезпечують корисні інструменти для оцінки впливу додавання (вилучення) вектора на зниження (підвищення) таких відстаней. А саме, як слідує з (2.7), видалення 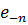 із
із  не буде збільшувати відстань від
не буде збільшувати відстань від  з
з 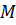 якщо
якщо 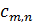 рівне нулю. Аналогічно з (2.9), додавання
рівне нулю. Аналогічно з (2.9), додавання  до
до  не зменшить
не зменшить  якщо
якщо 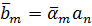 . Ці факти швидше за все мають цікаву інтерпретацію результатів у статистиці (див. [16], [14]). Було б корисно привести кілька конкретних прикладів оціночних функцій
. Ці факти швидше за все мають цікаву інтерпретацію результатів у статистиці (див. [16], [14]). Було б корисно привести кілька конкретних прикладів оціночних функцій  або ж стаціонарних процесів, які відображають ці феномени.
або ж стаціонарних процесів, які відображають ці феномени.
|
|
|
2.8 результати і доведення для 
В цьому розділі для комплексно значної матриці 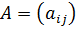 , ми писатимемо
, ми писатимемо  для матриць
для матриць  відповідно. Використовуючи зовнішню функцію
відповідно. Використовуючи зовнішню функцію 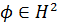 , ми визначаємо
, ми визначаємо 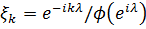 , де
, де 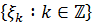 це повний ортонормований базис
це повний ортонормований базис 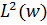 такий, що
такий, що
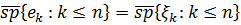
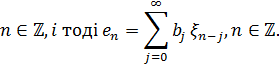
Ми виражаємо різні проекції в термінах  .
.
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 363; Нарушение авторских прав?; Мы поможем в написании вашей работы!