Уравнение Лэнгмюра

Задачи

1. С помощью нефелометра сравнивают светорассеяние стандартного и исследуемого гидрозолей мастики равных концентраций. Интенсивности рассеянных световых потоков одинаковы при высоте освещенной части исследуемого золя h₁ =5 нм и высоте стандартного золя h₂ =21 нм. Средний радиус частиц стандартного золя 120 нм. Рассчитайте радиус частиц исследуемого золя.

2. Определите диаметр частиц аэрозоля, используя результат исследо­вания методом поточной ультрамикроскопии: в объеме 2,2•10^-2 мм³ подсчитано 87 частиц аэрозоля (дыма мартеновских печей). Концентрация аэрозоля 1•10^-4 кг/м³, плотность дисперсной фазы 2 г/см³, форма частиц сферическая.

3. С помощью нефелометра сравнивались мутности двух гидрозолей мастики равных концентраций. Полу­чены следующие экспериментальные данные; мутности определяемого и стандартного золей стали одинаковыми, при высоте освещенной части первого золя h_1: = 5-10^-3 кг/м³. и высоте второго золя h₂ = 19,0-10^-3 м. Средний радиус частиц стандартного золя r₁= 120-10^-9 м. Определить радиус частиц г₂ второго золя.

4. Используя уравнение Рэлея, сравните интенсивности света, рас сеянного двумя эмульсиями с равными радиусами частиц и концентрациями: бензола (n₁, ==1,501) в воде и н-пентана (n₁ = 1,357) в воде. Показатель преломления воды п₀ = 1,333.

5. Покажите, в каком случае и во сколько раз интенсивностьрассеянного дисперсной системой света больше: при освещении синим светом (λ₁=410 нм) или красным светом (λ₂=630 нм). Светорассеяние происходит в соответствии с уравнением Рэлея, и интенсивности из дающих монохроматических пучков света равны.

6. В каком случае и во сколько раз интенсивность све­торассеяния латекса полистирола больше: при освещении светом с λ1 = 530-10-9 м. или с λ2= 680-10-9м.

7. Методом поточной ультрамикроскопии в объемеW = l,5-10-11 м3 подсчитано 53 частицы аэрозоля масляного тумана. Считая форму частиц сферической, определить их средний радиус. Концентрация золя с = 21·10-6 кг/м3,плотность γ = 0,92-103. кг/м3.

8. С помощью метода поточной ультрамикроскопии в! объеме W=2·10-11 м3 подсчитано 80 частиц аэрозоля—дыма мартеновских печей. Концентрация аэрозоля с = 10·10-5 кг/м3, плотность γ = 2-103 кг/м3. Определить среднюю длину ребра частицы l, считая ее форму кубической.

9. Сравнить интенсивности светорассеяния высокодисперсного полистирола, освещенного монохроматическим светом с длинной волны λ1=680-10-9 м, а затем с длиной волны λ2 =420-10-9 м (α =4).

10. Используя уравнение Рэлея, сравнить интенсивности светорассеяния двух эмульсий с равными радиусами части! и концентрациями: бензола в воде (показатель преломления n=1,50) и н-пентана в воде (п1 = 1,36). Показателе преломления воды п0 = 1,33.

11. Сравнить интенсивности светорассеяния эмульсий бензина в воде (показатель преломления п1 = 1,38) и тералина в воде (п1 = 1,54) при 293°. Показатель преломления воды n0 = 1,33. Размер частиц и концентрация эмульсий одинаковы.

12. При исследовании гидрозоля золота методом точной ультрамикроскопии в объеме W = l,6·10-11 подсчитано 70 частиц. Определить средний радиус частиц золя, приняв их форму за сферическую. Весовая концентр рация золя с = 7·10-6 кг/м3, плотность γ= 19,3·103 кг/м3.

13. При исследовании аэрозолей методом поточной ультрамикроскопии, в объеме W = 1,33·10-11 м3, протекшем через счетное поле микроскопа, подсчитано 50 частиц масляного тумана. Определить средний радиус частиц, приняв их форму за сферическую. Весовая концентрация аэрозоля c = 25·10-6 кг/м3, плотность γ=0.9·103 кг/м3.

14. Рассчитать средний радиус частиц гидрозоля латек­са полистирола, пользуясь данными, полученными с по­мощью нефелометра: высота освещенной части стандарт­ного золя h1 = 8-10~3 ж, средний - радиус частиц rх = 88-10-9 м, высота освещенной части неизвестного золя hz = 18-10-3 м. Концентрации стандартного и неизвест­ного золя равны.

15. При ультрамикроскопическом исследовании гид­розоля серебра в кювете площадью 5,4·10-12 м2 и глуби­ной пучка света 2,5·10-4 м подсчитано 2 частицы. Рас­считать среднюю длину ребра частиц, принимая их форму за кубическую. Концентрация золя с=20·10-2 кг/м3, плотность серебра γ=10,5·103 кг/м3.

16. С помощью метода поточной ультрамикроскопии в: прошедшем объеме W = 2·10-11 м3 подсчитано 100 частиц; золя серы. Концентрация золя с = 6,5·10-5 кг/м3, плот­ность γ = 1·103кг/м3. Рассчитать средний радиус час­тиц, приняв их форму за сферическую.

17. Методом поточной ультрамикроскопии в объеме W=3·10-11 м3 подсчитано 60 частиц аэрозоля водяного тумана. Каков средний радиус частиц, если концентрация аэрозоля с =15·10-6 кг/ж3? Форму частиц принять за сферическую.

18. При исследовании гидрозоля золота с помощью ультрамикроскопа в видимом объеме W =12·10-19 м3 подсчитано 5 частиц. Приняв форму частиц за шарообраз­ную, рассчитать их средний радиус. Концентрация золя с= 30·10-2 кг/м3, плотность золота γ = 19,3·103 кг/м3.

19. При изучении ослабления синего света золями мастики получены следующие данные:

Концентрация золя, % (масс.)	0,60	0,20	0,03	0,04
Толщина слоя, мм.	2,5	2,5
Доля прошедшего света, %	3,1	29,4	2,6	15,9

Покажите применимость уравнения Бугера — Ламберта — Бера для этой дисперсной системы. Рассчитайте, какая доля света будет рассеяна 0,25%-ным золем при толщине поглощающего слоя равно 10мм.

20. Рассмотрите возможность применения уравнения Бугера—Лам-берта—Бера для гидрозолей гидроксида железа, используя данные по ослаблению монохроматического света (λ = 500 нм) этими дисперсными системами:

Концентрация золя, % (масс.)	0,20	0,10	0,08	0,04	0,02
Толщина слоя, мм	2,5	2,5	2,5	5,0	5,0
Доля прошедшего света, %.	1,7	11,8	18,6	18,2	43,0

Определите, какая доля света будет рассеяна 0,02%-ным золем, находящимся в кювете длиной 30 мм.

21. Два пучка монохроматического света равной начальной интенсивности с λ₁=440 нм (синий свет) и λ₂=630 нм (красный свет) проходят через эмульсию бензола в воде. Рассчитайте отношение интенсивностей прошедшего света, если толщина слоя эмульсии равна а) 1 см; б) 5 см; в) 10 см. Содержание дисперсной фазы 0,10% (об.) средний радиус частиц эмульсии 40 нм, показатель преломления бензола и воды соответственно п₁ = 1,501 и n₀ = 1,333. При расчете примите, что ослабление света происходит только в результате светорассеяния, и показатели преломления не зависят от длины волны света.

22. Свет с длиной волны 540 нм и начальной интенсивностью I₀ проходит через слой эмульсии тетралина в воде толщиной:

а) 5 см

б) 10 см;

в) 15 см;

Рассчитайте долю прошедшего света I_n/I₀ и постройте график зависимости ее от радиуса частиц дисперсной фазы, изменяющегося в результате опалесценции от 10 до 50 нм. Содержание дисперсной фазы 0,05 % (масс.)., показатель преломления тетралина и воды п₁ = 1,540, n₀ = 1,333.

23. Рассчитайте радиус частиц полистирольного латекса (варианты I — IV) по зависимости оптической плотности D от длины волны света λ:

	D
λ, нм	I	II	III	IV
	0,562	0,900	0,795	—
	0,414	0,704	0,566	—
	0,289	0,518	0,382	0,336
	0,207	0,387	0,267	0,266
	0,159	0,306	0,202	0,221
	0,120	0,237	0,150	0,180

При расчете используйте уравнение Геллера.

24. Исходя из значений оптической плотности D_λ1 = 0,023 и D_λ2 =0,135, полученных с помощью фото­электрического колориметра ФЭК для длин волн: λ₁ = 680-10^-9 м и λ₂ = 420-10^-9 м, и используя калибро­вочную кривую Геллера, найти сред­ний радиус частиц гидрозоля латекса.

25. Проверить графически применимость закона Лам­берта — Бера к гидрозолю кубового синего красителя, используя экспериментальные данные спектрофотометрического метода:

Концентрация золя

с- 103, кг/м3 …….20.0 40.0 60.0 70.0

Оптическая плотность

Dλ……………….0.20 0.38 0.55 0.67

26. Пользуясь экспериментальными данными спектрофотометрических измерений, подтвердить графически применимость закона Ламберта — Бера к гидрозолю сернистого черного красителя и определить концентрацию золя при d_λ = 0,55.

Концентрация золя

с-10³кг/м³ 20.0 40.0 60.0 80.0 100.0 120

Оптическая плотность

D_λ… ……0.15 0.30 0.43 0.60 0.78 0.92

Глава 4. Поверхностные явления

Термодинамические функции поверхностного слоя

Поверхностный, межфазный слой представляет собой область постепенного (плавного) изменения свойств, при переходе от одной фазы системы к другой. Также постепенно меняется структура поверхностного слоя – от структуры одной фазы до структуры другой фазы. Образование поверхностного слоя есть результат взаимодействия смежных фаз. Изменения свойств и структуры поверхностного слоя обусловлены действием поверхностной энергии.

При постоянной температуре и давлении поверхностная энергия Гиббса определяется произведением поверхностного натяжения (фактор интенсивности) s на площадь поверхности (фактор емкости ) s:

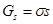(1)

Плотность поверхности зависит от ее кривизны и дисперсности фаз. Дисперсность D линейно связана с удельной поверхностью S_уд:

где – V – объем дисперсной фазы, мл; k – коэффициент формы частиц; d -диаметр частицы, м².

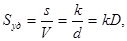(2)

(3)

Для сферических частиц уравнение принимает вид:

Для расчета удельной поверхности (S_уд) системы с шарообразными частицами достаточно знать величину среднего радиуса частицы:

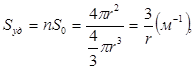(4)

где n – число частицы, м³; S₀ – поверхность каждой частицы. Или

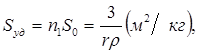(5)

где n₁ – число частиц, кг; r - плотность вещества, г/см³.

Кривизна поверхности H в данной точке определяется производной площади поверхности по объему:

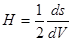(6)

или с помощью соотношения

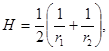(7)

где r₁ и r₂ – радиусы окружностей, получаемых при пересечении, проходящими через нормаль к ней в данной точке двумя перпендикулярными плоскостями.

Поверхностное натяжение можно представить как энергию переноса молекул из объема тела на поверхность или как работу образования единицы поверхности. Поверхностное натяжение можно выразить частной производной от энергии Гиббса по величине межфазной поверхности при p и T=const (при постоянных числах молей компонентов):

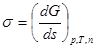(8)

Размерность поверхностного натяжения Дж/м² или н/м. Известно несколько методов определения поверхностного натяжения.

Методы измерения поверхностного натяжения

При использовании метода поднятия жидкости в капилляре применяют следующие уравнения:

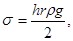(9)

где s - поверхностное натяжение жидкости, н/м; r – радиус капилляра, м; r - плотность, кг/м³; g – ускорение силы тяжести, м/сек²).

Другой метод определения поверхностного натяжения – метод Траубе. С помощью сталагмометра подсчитывается, какое число капель стандартной жидкости n₀ и исследуемой жидкости n_x содержится в определенном объеме этих жидкостей:

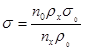(10)

где g₀ и g_x – плотности стандартной и исследуемой жидкостей, s₀ – поверхностное натяжение стандартной жидкости.

Также применяется метод «отрыва кольца». Здесь определяют усилие, которое нужно приложить, чтобы преодолеть силу сцепления кольца с жидкостью и оторвать кольцо от поверхности. Величина силы F выраженная в кг, пропорциональна поверхностному натяжению s (н/м):

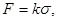(11)

где k – обобщенная константа, зависящая от диаметра проволоки, размеров кольца и краевого угла смачивания q. Величину k определяют по стандартной жидкости, поверхностное натяжение которой известно, - обычно по воде.

Распространен метод определения поверхностного натяжения – метод наибольшего давления пузырька, предложенный П. А. Ребиндером. Давление, при котором пузырек проскакивает через поверхностную пленку жидкости и прорывает ее, определяется величиной поверхностного натяжения жидкости:

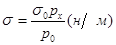(12)

где s₀ – поверхностное натяжение стандартной жидкости, н/м; p_x и p₀ – необходимые для проскока пузырька через поверхность исследуемой и стандартной жидкости, н/м².

Изменение поверхностного натяжения раствора при введении поверхностно – активных веществ (ПАВ) определяют с помощью уравнения Шишковского:

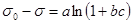(13)

где s₀ – поверхностное натяжение растворителя (н/м), s - поверхностное натяжение раствора, a и b – эмпирические константы, причем величина a мало меняется от вещества к веществу, а b зависит от поверхностной активности вещества, c - концентрация раствора (кмоль/м³).

Внутренняя (полная) энергия поверхностного слоя

Внутренняя (полная) энергия поверхностного слоя U_s (в расчете на единицу площади) связана с s уравнением Гиббса – Гельмгольца:

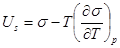(14)

или

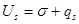(15)

где q_s – теплота образования единицы (индекс s означает отнесение параметра к единице площади поверхности); T – температура, К.

Явления капиллярности и смачивания

Изменение кривизны поверхности (удельной поверхности) вызывает изменение внутреннего давления в теле. Связь капиллярного давления с кривизной поверхности описывается уравнением Лапласа:

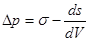(16)

С изменением кривизны поверхности меняется также давление пара над веществом. Связь между этими параметрами находит выражение в уравнении капиллярной конденсации Кельвина (Томпсона):

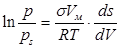(17)

где p и p_s – давление насыщенного пара: над поверхностью, имеющей кривизну и над ровной поверхностью. Соответственно, Па; V_м – мольный объем вещества в конденсированном состоянии, мл; R – универсальная газовая постоянная.

Работа адгезии (прилипания) W_{a ,} характеризующая взаимодействие фаз (она отнесена к единице площади поверхности), определяется уравнением Дюпре:

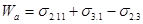(18)

где s_2.1 – поверхностное натяжение твердого тела или жидкости 2 на границе с газом 1; s_3.1 – поверхностное натяжение жидкости иди твердого тела 3 на границе с газом 1; s_2.3 – поверхностное (межфазное) натяжение на границе конденсированных фаз. Следовательно, чем больше работа адгезии, тем меньше межфазное натяжение s_2.3.

Взаимодействие между жидкой и другой конденсированной фазой можно оценить также с помощью краевого угла (угла смачивания) q, определяемого уравнением Юнга:

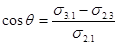(19)

Если сложить эти выражения, то получим уравнение Дюпре – Юнга, которое позволит рассчитать работу адгезии (по экспериментально определенному cos q):

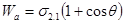(20)

Работа когезии определяется как работа необходимая для разрыва однородной объемной фазы (отнесенная к единице поверхности):

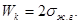(21)

Коэффициент растекания рассчитывается по формуле:

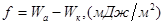(22)

Адсорбция

Величину адсорбции обычно выражают двумя способами:

а) абсолютная величина адсорбции:

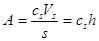(23)

где – c_s – концентрация компонента в поверхностном слое (моль/мл), имеющим объем V_s (мл) и толщину h (мм).

б) избыточная адсорбция:

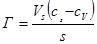(24)

или

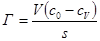(25)

где c_V – равновесная концентрация компонента в объеме (моль/мл); c₀ – исходная концентрация компонента в объеме (моль/мл); V – объем фазы (мл). Сравнивая уравнения (1.20) и(1.21), получим связь между величинами адсорбции А и Г:

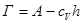(26)

Для определения количества адсорбирующего вещества могут применяться следующие уравнения:

1) уравнение Гиббса, устанавливающее соотношение между величиной адсорбции Г (кмоль/м²), концентрацией c (кмоль/м³) и мерой поверхностной активности (-ds/dc):

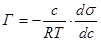(27)

где R – газовая постоянная, T – температура, К.

2) уравнение монослойной адсорбции Ленгмюра:

(28)

где Г – величина адсорбции (кмоль/м²); Г_¥ предельное количество адсорбирующегося вещества (кмоль/м²); b – константа, характеризующая поверхностную активность вещества (ее значение то же что и в уравнении Шишковского); c – равновесная концентрация растворенного вещества (кмоль/м³).

3) при адсорбции газа или растворенного вещества на твердом адсорбенте используют эмпирическое уравнение Френдлиха:

а) для растворов:

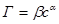(29)

б) для газов:

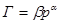(29)

4) уравнение для полислойной адсорбции разработано М. М. Дубининым. Уравнение изотермы на адсорбентах с мелкими порами (средний радиус порядка 10^-9 м):

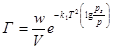(30)

а для крупнопористых адсорбентов (средний радиус порядка 10^-7 – 10^-6 м):

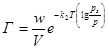(31)

где Г – величина адсорбции (кмоль/кг ), w – общая пористость (м³/кг), V – молярный объем адсорбируемого вещества в жидком состоянии (м³/кмоль). T – температура (К ), k₁ и k₂ – константы, p – равновесное давление пара при температуре (н/м²), p_s – давление насыщенного пара (по справочнику) (н/м²).

Примеры решения задач

1.Опредилите энергию Гиббса G_s поверхности капель водяного тумана массой m = 4 г при 293 К, если поверхностное натяжение воды s = 72.7 мДж/м², плотность воды

r = 0,998 г/см³, дисперсность частицы D = 50 мкм^–1.

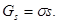Решение: Энергия Гиббса поверхности определяется по уравнению (1):

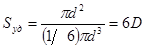Связь между удельной поверхностью s_уд, поверхностью s, объемом V и дисперсностью D выражается соотношением (3):

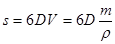Отсюда поверхность капель тумана составляет:

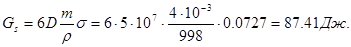и

2. Рассчитайте полную поверхностную энергию 5 г эмульсии бензола в воде с концентрацией 75 % (масс.) и дисперсностью D = 2 мкм^–1 при температуре 313 К. Плотность бензола при этой температуре r =0.858 г/см³, поверхностное натяжение

s = 32.0 мДж/^м2, температурный коэффициент поверхностного натяжения бензола

ds/dT = -0.13 мДж/(м²К).

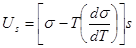Решение: Полная поверхностная энергия U_s рассчитывается по уравнению Гиббса – Гельмгольца (1.13):

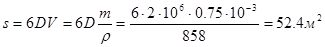Поверхность s капель бензола 75 % эмульсии массой m =5 г составляет:

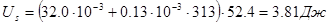Отсюда

3. Рассчитайте давление насыщенных паров над каплями воды с дисперсностью

D = 0.1 нм^–1 при температуре 293 К. Давление паров воды над плоскостью поверхностью при этой температуре p_s = 2338 Па, плотностью воды r = 0.998 г/см³, поверхностное натяжение воды s =72.7 мДж/м².

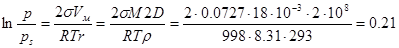Решение: Влияние кривизны поверхности на давление насыщенного пара выражается уравнением Кельвина (1.16):

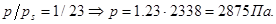Отсюда

4.Дае вертикальные параллельные пластинки частично погружены в жидкость на расстоянии d = 1 мм друг от друга. Угол смачивания q пластинок жидкостью составляет 30°. Поверхностное натяжение жидкости s = 65 мДж/м², разность плотностей жидкости и воздуха r = 1 г/см³.Рассчитайте избыточное давление в жидкости и силу взаимного притяжения пластинок, если их размеры составляют 5*5 см.

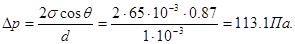Решение: Капиллярное (избыточное) давление в жидкости между параллельными пластинками рассчитывают по уравнению

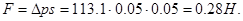При смачивании поверхности пластинок избыточное давление уменьшает внутреннее давление в жидкости, что приводит к ее падению по сравнению с уровнем жидкости в сосуде и появлению силы, прижимающей пластины:

Такую силу надо приложить к каждой пластинке перпендикулярно ее поверхности, чтобы оторвать пластинки друг от друга.

5.В воздухе, содержащем пары воды, образуется туман при температуре 270.8 К (коэффициент пресыщения g равен 4.21). Рассчитайте критический размер ядер конденсации и число молекул, содержащихся в них. Поверхностное натяжение воды s = 74 мДж/м², мольный объем V м = 18*10^–6 м²/моль.

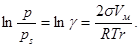Решение: Радиус r равновесного зародыша в зависимости от пресыщения системы определяется по уравнению Кельвина (1.16)

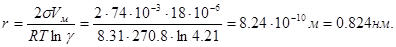Отсюда

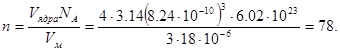Число молекул в одном зародыше составит:

6. Рассчитайте работу адгезии Wа ртути к стеклу при293К, если известен краевой угол

q = 130°. Поверхностное натяжение ртути s =475 мДж/м² . Найдите коэффициент растекания f ртути по поверхности стекла.

Решение: Выражение для работы адгезии через краевой угол дается уравнением Дюпре – Юнга (1.19):

Коэффициент растекания рассчитывается по соотношению f =W_a-W_к, где W_к = 2 s_Hg представляет работу когезии; f = 171 - 2 * 475 = - 779 мДж/м², т. е. растекания нет.

Задачи

1. Определите энергию Гибсса поверхности 5 г тумана воды, если поверхностное натяжение капель жидкости составляет 71.96 мДж/м², а дисперсность частиц 60мкм^-1.плотность воды примите равной 0.997 г/см³.

2. Аэрозоль ртути сконденсировался в виде большой капли объемом 3.5 см³.Определите, насколько уменьшилось поверхностная энергия ртути, если дисперсность аэрозоля составляла 10 мкм^-1

3. Определите поверхностное натяжение бензола при 293,313 и 343 К.. Примите, что полная поверхностная энергия не зависит от температуры и для бензола равна 61.9 мДж/м^2.температурный коэффициент ds/dT = 0.13 мДж/ (м²*К).

4. Рассчитайте полную поверхностную энергию 5 г эмульсии бензола в воде с концентрацией 55% (масс.) и дисперсностью 3 мкм³ при температуре 313 К. Плотность бензола 0.858 г/см³, межфазное поверхностное натяжение 26.13 мДж/м², температурный коэффициент поверхностного натяжения бензола ds/dT = -0.13 мДж/ (м²*К).

5. Рассчитайте избыточное давление внутри капель бензола, равновесных с паром, если удельная поверхность системы составляет 6*10^8 м^-1, а поверхностное натяжение безола 28.87 мДж/м² при293 К.

6. Рассчитайте избыточное давление в капле воды (за счет кривизны) с удельной поверхностью 3*10⁶ м^-1 при температуре 313 К, если поверхностное натяжение воды при 298 К составляет 71.96 мДж/м², а температурный коэффициент поверхностного натяжения воды ds/dT = 0.16 мДж/ (м²*К).

7. Рассчитайте капиллярное давление в ртути с дисперсностью 1мкм^-1, если поверхностное натяжение ртути составляет 0.475 Дж/м².

8. Чтобы стряхнуть ртуть в медицинском термометре, нужно создать ускорение, равное 10g. Рассчитайте диаметр перетяжки в капилляре термометра, если поверхностное натяжение ртути 0.475 Дж/м², длина столбика ртути выше перетяжки 5 см, плотность ртути 13.54 г/см³.

9. Найдите поверхностное натяжение жидкости, если в капилляре с диаметром 2 мм она поднимается на высоту 15 мм. Плотность жидкости 0.998 г/см³, краевой угол мениска равен 0°.Сделайте предположение о природе жидкости.

10. Для определения поверхностного натяжения воды взвешивают капли, отрывающиеся от капилляра, и измеряют, диаметр капли в момент ее отрыва. Оказалось что масса 318 капель воды равна 5 г, а диаметр шейки капли – 0.7 мм. Рассчитайте поверхностное натяжение воды.

11. Покажите, чему равна разность h₁-h₂ воды в двух сообщающихся капиллярах с диаметрами d₁ и d₂. Плотность и поверхностное натяжение жидкости равны соответственно r, s, краевые углы менисков равны нулю

12. Насколько изменится разность уровней воды в двух сообщающихся капиллярах с диаметрами0.1 и 0.3 мм при нагревании от 293 до 343 К, если поверхностное натяжение при этих температурах равно соответственно 72.75 и 64.0 мДж/м².Плотность воды при 293 и 343 К составляет соответственно 0.998 г/см³ и 0.78 г/см³.

13. Поверхностное натяжение жидкости, смачивающей стекло, измеряют, определяя высоту между уровнями двух менисков в U – образной капиллярной трубке; диаметры капилляров колен трубки равны 1 и10 мм. Рассчитайте поверхностное натяжение жидкости с плотностью 0.998 г/см³, зная, что разность двух уровней менисков в капиллярах составляет 9 мм.

14. На какую высоту поднимается вода между двумя вертикальными стеклянными пластинками, частично погруженными в эту жидкость, если расстояние между ними 0.5 мм? Плотность и поверхностное натяжение воды соответственно равны 0.997 г/см³ и71.96 мДж/м². Краевой угол q примите равным 0°.

15. Вычислите поверхностное натяжение воды, определяемое методом капиллярного поднятия, если при 298 К вода поднялось в капилляре на высоту 35.3 мм. Диаметр капилляра определен путем измерения длины столбика и массы ртути, заполнявшей капилляр под давлением6 длина столбика ртути составила 8.04 см, масса его 0.565 г. Плотность ртути 13.54 г/см³, плотность воды 0.997 г/см³.

16. Между двумя параллельными пластинками находятся слой воды толщиной 0.5 мкм. Рассчитайте давление, сжимающее пластины. Если угол смачивания q = 0°, поверхностное натяжение воды равно 71.96 мДж/м². Определите силу, которую необходимо приложить для отрыва пластин друг от друга, если размер каждой 10*10 см.

17. Капли воды массой 0.1 г введена между параллельными стеклянными пластинками, причем краевой угол q = 0°. Какова сила притяжения между пластинками, если они находятся друг от друга на расстоянии 1 мкм. Поверхностное натяжение воды составляет 71.96 мДж/м², плотность воды 0.997 г/см³.

18. С какой силой притягиваются две вертикальные и параллельные стеклянные пластинки, частично погружены в воду, если расстояние между ними равно 1 мм? Ширина пластинок 15 см, поверхностное натяжение воды 71.96 мДж/м², угол смачивания 0°. Высота пластинок такова, что поднявшаяся вода не доходит до их верхних краев. Плотность воды примите равной 0.997 г/см³.

19. Определите, насколько давление паров над каплями воды диаметром 0.2 мкм больше, чем давление паров над плоской поверхностью при температуре 298 К. Поверхностное натяжение

воды 71.96 мДж/м², мольный обьем воды 18.05 см³/моль. Как изменится это давление. Если дисперсность капель увеличится в 10 и100 раз?

20. Оцените размер частиц SrSO₄, зная, что их растворимость на 3% (масс.) больше растворимости крупных кристаллов. Межфазное натяжение при 298 К примите равным 85 мДж/м², плотность SrSO₄ 3.96 г/см³.

21. Рассчитайте межфазное расстояние в системе CaF₂ – вода, зная, что растворимость частиц CaF₂ диаметром 0.3 мкм превышает растворимость крупных кристаллов (при 293 К) на 18% (масс.). Плотность CaF₂ примите равной 2.5 г/см³.

22. Найдите поверхностное натяжение анилина, если с помощью сталагмометра Траубе получены следующие данные: число капель анилина 42, плотность его r = 1.4*10^-3 кг/м³, число капель воды 18. Температура опыта 288 К. поверхностное натяжение воды s0 = 73.26*10^-3н/м.

23. Во сколько раз изменится запас свободной поверхностной энергии водяного тумана, если радиус его капелек увеличится от 1*10^-6 до 1.2*10^-3 м при 288К.

24. Вычислите удельную поверхность золя сернистого мышьяка, средний диаметр частицы которого равен 120*10^-9 м, а плотность r = 3.43*10³ кг/м³ (ответ дайте в м^-1 и м²/кг).

25. Определите величину удельной поверхности суспензии каолина (плотность которого r = 2.5*10³ кг/м³), если ее частицы принять шарообразными и средний диаметр частиц равным 0.5*10^-6 м? Суспензию считать монодисперсной.

26. Для водного раствора пропилового спирта найдены следующие значения констант уравнения Шишковского (при 293°): a = 14.4*10^-3, b = 6.6. Вычислите поверхностное натяжение раствора с концентрацией, равной 1 кмоль/м³. Поверхностное натяжение воды s₀ = 72.53*10^-3 н/м.

27. Даны константы уравнения Шишковского для водного раствора валериановой кислоты при273К: a = 14.72*10^-3, b = 10.4. При какой концентрации поверхностное натяжение раствора будет составлять 52.1*10^-3н/м, если поверхностное натяжение воды при273 К равно

75.49*10^-3н/м.

28 Используя константы уравнения Шишковского (a = 12.6*10^-3,b = 21.5), рассчитать поверхностное натяжение для водных растворов масляной кислоты при 273 К для следующих

концентраций (кмоль/м³): 0,007, 0.021,0.05.0.104 и построить кривую в координатах s = f(c). Поверхностное натяжение воды s₀ = 75.49*10 ^-3н/м.

29. Определите поверхностную активность уксусноэтилового эфира по приведенным ниже значениям поверхностного натяжения водных растворов его при 298 К:

С ммоль/л 7.8 15.6 31.2 62.5 125 250 500

s, мДж/м² 69.6 68.0 65.1 61.5 56.2 49.7 41.5.

Постройте изотерму гиббсовской адсорбции. Поверхностное натяжение воды 71.96 мДж/м².

30. Вычислите адсорбцию масляной кислоты на поверхности раздела водного раствора с воздухом при 273К и концентрации c = 0/1 кмоль/л³, если зависимость поверхностного натяжения от концентрации выражается уравнением Шишковского:

31

Найдите адсорбцию пропионовой кислоты на поверхности раздела водный раствор – воздух при 273К и концентрации 0.5 кмоль/м³ по константам Шишковского: a = 12.5*10^-3 и b = 7.73.

32 Вычислите адсорбцию масляной кислоты на поверхности раздела водный раствор – воздух при 283К и концентрации c = 0.104 кмоль/м³, используя следующие экспериментальные данные. Концентрация

c,кмоль/м³: 0.00 0.021 0.050 0.104 0.246 0.489

Поверхностное

натяжние s*10³, н/м:74.01 69.51 64.30 59.85 51.09 44.00.

33. Используя уравнение Ленгмюра, вычислить адсорбцию пропионовой кислоты на поверхности раздела водный раствор – воздух при 293К и концентрации с = 0.1 кмоль/м³, если известны константы уравнения Шишковского: a = 12.8*10^-3, b = 7.16.

34.Вычислите по формуле Ленгмюра величину адсорбции изоамилового спирта концентрации c= 0.1 кмоль/м³ на поверхности раздела водный раствор – воздух при 292К по данным константам: Г_¥ = 8.7*10^-9 кмоль/м², b = 42.

35 Используя уравнение Ленгмюра, вычислить величину адсорбции азота на цеолите при давлении p = 2.8*10², Г_¥ = 38.9*10^-3кг/кг, а b = 0.156*10^-2.

36 Найти площадь, приходящуюся на одну молекулу в насыщенном слое анилина на поверхности его водного раствора, если предельная адсорбция Г_¥ = 6.0*10^-9 кмоль/м? Рассчитайте работу адгезии для воды, глицерина, трикрезилфосфата и бензола, которые смачивают фторопласт. Поверхностное натяжение (на границе с воздухом) воды, глицерина, трикрезилфосфата и бензола соответственно равны 71.96; 63.2; 40.9; 28.9 мДж/м², а краевые углы составляют 108, 100, 75 и 46°.

37 Рассчитайте работу адгезии в системе вода – графит, зная, что краевой угол равен 90°, а поверхностное натяжение воды составляет 71.96 мДж/м². Определите коэффициент растекания воды на графите.

38 Рассчитайте работу адгезии ртути к стеклу при 293 К, если известен краевой угол q = 130°. Поверхностное натяжение ртути 475 мДж/м². Найдите коэффициент растекания ртути по поверхности стекла.

39 Краевой угол воды на парафине равен 111° при 298 К.. Для 01 M раствора бутиламина в воде поверхностное натяжение составляет 56.3 мДж/м², краевой угол на парафине равен 92°. Рассчитайте поверхностное давление пленки бутиламина, адсорбированного на поверхности раздел парафин – вода. Поверхностное натяжение воды 71.96 мДж/м².

40 По константам уравнения Ленгмюра Г_¥ = 182*10^-3 и b = 0.1*10^-2 рассчитать и построить кривую адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10*10^-2 - 400*10² н/м².

41 Используя константы эмпирического уравнения Фрейндлиха b = 1.6*10^-3 и a = 0.48, построить кривую адсорбции углекислого газа на активированном угле при 271 К в интервале давлений от 2*10² до 30*10² н/м².

42 Вертикально установленная капиллярная трубка с внутренним диаметром d = 3*10² мкм одним концом погружена в жидкость на глубину h = 3 см, а вторым соединена сосудом, в котором поддерживается избыточное давление. Определить, при каком давлении в сосуде будет происходить отрыв пузырька воздуха от нижнего, погружети с диспидкость конца капилляра. Поверхностное натяжение и плотность жидкости соответственно равны s = 72*10^-3 н/м и r =1*10³ кг/м³.

43 Рассмотрите возможность растекания водного раствора валериановой кислоты по поверхности ртути, исходя из значений поверхностных и межфазных натяжений: s_{р-р-воздух} = 25 мДж/м²,

s_{Hg-воздух} = 475 мДж/м², s_Hg-р-р = 329 мДж/м². Если раствор будет растекаться по поверхности ртути, то, как при этом ориентируются полярные группы валериановой кислоты: к воде или к ртути? Объясните почему.

Глава 5. Адсорбция газов и паров на поверхности твердых тел. Адсорбция из растворов на поверхности твердых тел

.

При адсорбции газов и паров на поверхности твердых тел (адсорбентов) возможно прямое экспериментальное определение удельной адсорбции по разности давлений газа до и после адсорбции. Удельную адсорбцию растворенных веществ на поверхности твердых тел также определяют экспериментально по изменению концентрации раствора до и после адсорбции.

В некоторых случаях при адсорбции газов толщина поверхностного слоя (слоя адсорбированного газа) равна размеру адсорбированных молекул. К таким системам применима теория мономолекулярной адсорбции Лэнгмюра.

Эта теория устанавливает следующую зависимость между удельной адсорбцией и равновесным давлением:

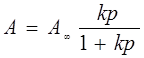(1)

А_∞ -предельно возможное значение удельной адсорбции при полном заполнении активных центров поверхности;

k- константа, пропорциональная энергии взаимодействия молекул газа с адсорбентом.

Для некоторых систем А_∞ численно равна удельной адсорбции, соответствующей образованию на поверхности адсорбента насыщенного монослоя.

Преобразуя уравнение (1) в линейное уравнение, получаем:

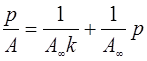(2)

Из уравнения (2) следует, что в случае применимости уравнения (1) изотерма адсорбции, построенная в координатах р/А=f(p), будет представлять собой прямую линию с угловым коэффициентом, равным 1/А_∞. Уравнение Лэнгмюра для адсорбции из растворов на поверхности твердых тел выглядит таким образом:

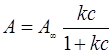, (3)

а линейная его форма:

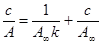. (4)

В данном случае изотерма адсорбции строится в координатах c/A=f(c) и будет представлять собой прямую линию с тем же коэффициентом.

В некоторых случаях применяется уравнение Ленгмюра вида:

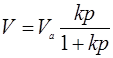(5)

Здесь Va – адсорбционный объем, V – равновесный объем адсорбата.

Дата добавления: 2015-08-31