
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Камеральні роботи при обробці результатів вимірювань мережі тріангуляції
При камеральних роботах дотримуються наступної послідовності:
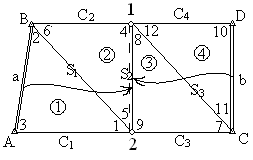
Рисунок. 2.1.
Як видно з рис. 2.1., в мережі виміряно 2 базиси: a i b та всі 3 кути в кожному трикутнику. Під час складання схеми мережі тріангуляції обов’язково нумерують трикутники і кути. 1-й трикутник починають з того трикутника, в якому заміряний базис, а далі - рахують по-порядку. Кути в трикутнику доцільно нумерувати за загальноприйнятою схемою. Всі сторони трикутника мають свою назву та сторони  ,
, 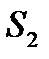 ,
, 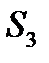 називають зв’язуючими сторонами, тому що вони є спільними для двох сусідніх трикутників.
називають зв’язуючими сторонами, тому що вони є спільними для двох сусідніх трикутників.
Сторони 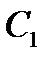 ,
, 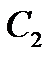 ,
,  ,
,  називають проміжними тому, що вони не є спільними з іншими трикутниками.
називають проміжними тому, що вони не є спільними з іншими трикутниками.
Нумерують кути в трикутника за наступним правилом:
1-й кут – проти виміряного базису а;
2-й – проти проміжної сторони;
3-й – проти зв’язуючої сторони 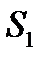 ;
;
Переходять до нумерації кутів у другому трикутнику:
4-й кут – проти 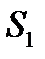 ;
;
5-й – проти проміжної сторони 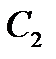 ;
;
6-й – проти зв’язуючої сторони  ;
;
Аналогічно в третьому трикутнику:
7-й кут – проти 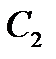 ;
;
8-й – проти проміжної сторони 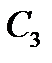 ;
;
9-й – проти  ;
;
В четвертому трикутнику:
кут 10 проти 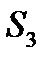 ;
;
11-й – проти проміжної сторони  ;
;
12-й – проти базису b.
Така нумерація кутів дозволяє майже автоматично складати базисне рівняння, яке має наступний вигляд:
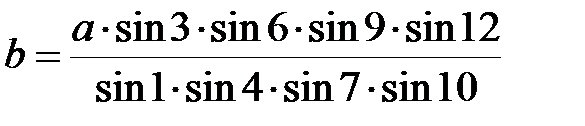
Складання базисного рівняння:
Із першого трикутника згідно теореми синусів:
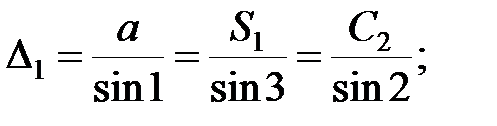
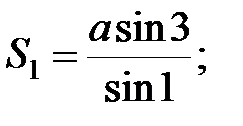
 ;
;



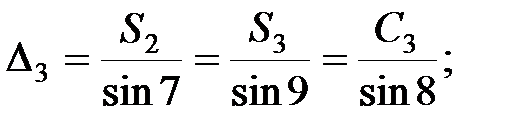
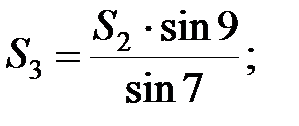

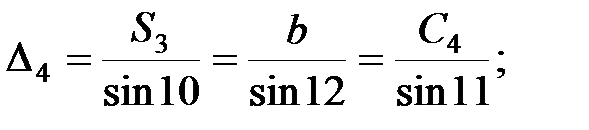

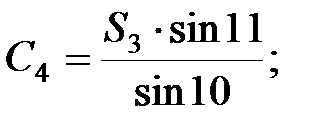

В мережі тріангуляції виникає стільки умов фігур скільки є трикутників. Оскільки в трикутнику вимірюються всі кути, то нев’язка визначається за формулою:

Поправка в виміряні кути вводиться порівну:

Гранична похибка нев’язки в трикутнику:
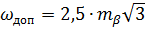
де  - СКП вимірювання горизонтального кута
- СКП вимірювання горизонтального кута
Вільний член базисної умови обчислюється за формулою:

Допустимий вільний член базисного рівняння обчислюється за формулою:
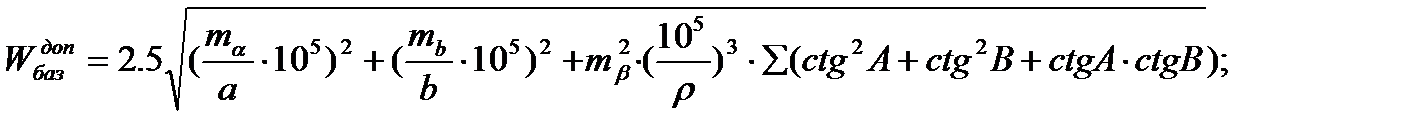
де  ,
, 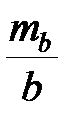 - відносні СКП вимірювання базисів
- відносні СКП вимірювання базисів
Якщо величина вільного члена базисного рівняння менше або рівне допустимої величини, то обчислюють величину вторинної поправки за формулою:
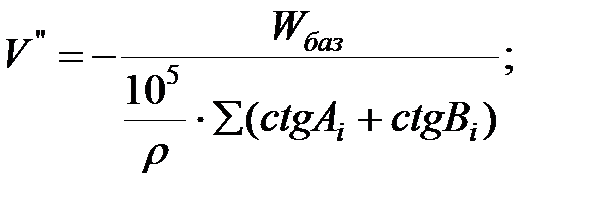
Вторинну поправку додають тільки до зв’язуючих кутів, при чому до кутів, які знаходяться в чисельнику базисного рівняння додають вторинну поправку з тим знаком, який отримали за формулою, а кути, які знаходяться в знаменнику базисного рівняння її додають з оберненим знаком. Слід пам’ятати, що поправки заокруглюють до 0,1́. Вторинна поправка вводиться з метою, щоб знайти теоретичне місце точки в якій перетинаються промені трикутника і не порушується теоретична умова.
Після цього за урівняними кутами обчислюють довжини сторін трикутників. Контролем обчислень являються рівності вирахуваного і виміряного значення базиса b.
Маючи урівняні кути і довжини ліній, обчислюємо прямокутні координати точок за формулами Юнга (рис.2.2.) або методом теодолітних ходів. 


Рисунок 2.2.
Контроль:

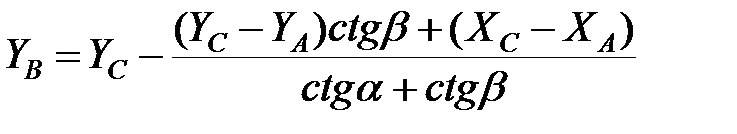
2.3. Виконати урівнювання мережі тріангуляції спрощеним методом 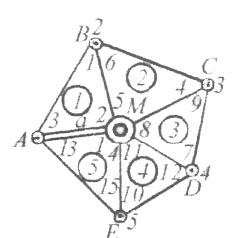
Вихідні дані:варіант 27
| 1=77°06,9' | 2=66°47,0' |
| 3=36°06,1' | 4=39°28,6' |
| 5=93°17,1' | 6=47°14,3' |
| 7=40°44,0' | 8=63°50,5' |
| 9=75°25,5' | 10=74°36,8' |
| 11=61°49,3' | 12=43°33,9' |
| 13=41°42,2' | 14=74°16,0' |
| 15=64°01,8' | а =129,93 м |
| αМА=27°21,4' | |
| Xм=2000,00 | Yм=3600,00 |
Рисунок.2.3.Схема мережі тріангуляції
mβ=1", а відстань базиса виміряна з точністю: 
Таблиця 2.1 - Рішення трикутників мережі тріангуляції
| № трик. | № кута | Виміряні кути | Поправки | Виправлені кути | Синуси кутів | Сторони | |
| V' | V'' | ||||||
| 77°06,9' | +3,87 | 77°6'57,87`` | 0,974829791 | 129,93 | |||
| 66°47,0' | 66°47' | 0,919020707 | 122,492 | ||||
| 36°06,1' | -3,87 | 36°6'2,13`` | 0,589204701 | 78,532 | |||
| ∑ | 180˚0,0' | 180˚00' | |||||
| W1 | 0˚0,0' | -3,87 | |||||
| 39°28,6 | +2,89`` | 39°28`38,87`` | 0,635774668 | 78,532 | |||
| 93°17,1' | 93°17,1`` | 0,998356852 | 123,318 | ||||
| 47°14,3' | +0,1 | -2,89`` | 47°14'15,11`` | 0,734174762 | 90,686 | ||
| ∑ | 179°59`54`` | 180˚00' | |||||
| W2 | 0˚0'06`/3 | -2,89`` | |||||
| 40°44,0' | +4,35`` | 40°44'4,35`` | 0,652555338 | 90,686 | |||
| 63°50,5' | 63°50'30`` | 0,897579204 | 124,738 | ||||
| 75°25,5' | -4,35`` | 75°25'25,65`` | 0,967813757 | 134,498 | |||
| ∑ | 180˚0,0' | 180˚0,0' | |||||
| W3 | 0˚0` | -4,35`` | |||||
| 74°36,8' | +4,67`` | 74°36'2,67`` | 0,964163182 | 134,498 | |||
| 61°49,3' | 61°49'18`` | 0,881482086 | 122,965 | ||||
| 43°33,9' | -4,67`` | 43°33'49,33`` | 0,689160638 | 96,136 | |||
| ∑ | 180˚0,0' | 180˚00' | |||||
| W4 | 0˚0,0' | -4,67`` | |||||
| 41°42,2' | +3,85`` | 41°42'15,85`` | 0,665287726 | 96,134 | |||
| 74°16,0' | 74°16,0' | 0,962534154 | 139,090 | ||||
| 64°01,8' | -3,85`` | 64°01'44,15`` | 0,89901528 | 129,927 | |||
| ∑ | 180˚00' | 180˚00' | |||||
| W5 | 0˚0,0' | -3,85`` |
|
|
Дата добавления: 2015-08-31; Просмотров: 650; Нарушение авторских прав?; Мы поможем в написании вашей работы!