
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделирование движения механической системы в силовом поле
|
|
|
|
Механическая система представляет собой совокупность материальных точек, взаимодействующих друг с другом и окружающими телами. Основная задача механики состоит в расчете движения точек системы, исходя из их масс и действующих на них сил. Эта глава посвящена компьютерному моделированию систем, состоящих из одной или нескольких частиц, взаимодействующих друг с другом и движущихся во внешнем силовом поле [3].
Простейшей механической системой является материальная точка, которая под действием некоторой силы движется вдоль прямой (например, оси 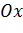 ). Если считать, что движение происходит в вязкой среде, а масса частицы и действующая на нее сила, зависят от координат и времени, то задача становится достаточно сложной. Пусть материальная точка массой m движется вдоль оси
). Если считать, что движение происходит в вязкой среде, а масса частицы и действующая на нее сила, зависят от координат и времени, то задача становится достаточно сложной. Пусть материальная точка массой m движется вдоль оси 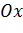 под действием силы
под действием силы 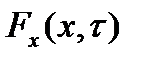 . На частицу также действует сила сопротивления, которая пропорциональна скорости:
. На частицу также действует сила сопротивления, которая пропорциональна скорости: 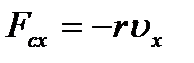 . В начальный момент точка имеет координату
. В начальный момент точка имеет координату  и скорость
и скорость 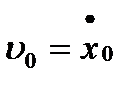 . Необходимо определить координату точки
. Необходимо определить координату точки 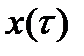 , ее скорость
, ее скорость  и ускорение
и ускорение  в следующие моменты времени [7]. Из второго закона Ньютона
в следующие моменты времени [7]. Из второго закона Ньютона 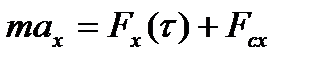 следует дифференциальное уравнение второго порядка:
следует дифференциальное уравнение второго порядка:  . Характер движения физической системы зависит от ее параметров, начальных условий и действующей на нее внешней силы. В этом случае возможны следующие ситуации:
. Характер движения физической системы зависит от ее параметров, начальных условий и действующей на нее внешней силы. В этом случае возможны следующие ситуации:
1) внешняя сила отсутствует;
2) внешняя сила постоянна;
3) внешняя сила изменяется по некоторому закону 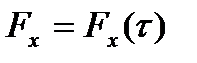 .
.
Будем использовать метод сеток, для этого перейдем от непрерывной области 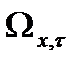 к дискретной области
к дискретной области 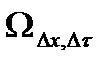 . В соответствии с методом Эйлера заменим бесконечно малые приращения функции
. В соответствии с методом Эйлера заменим бесконечно малые приращения функции 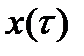 и ее первые две производные
и ее первые две производные 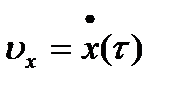 ,
,  их конечно–разностными аппроксимациями. Исходя из параметров системы (m и r), координаты
их конечно–разностными аппроксимациями. Исходя из параметров системы (m и r), координаты 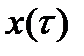 и скорости
и скорости  частицы в момент
частицы в момент  , рассчитываются ее координата и скорость в следующий момент
, рассчитываются ее координата и скорость в следующий момент  (дискретный момент
(дискретный момент  ):
): 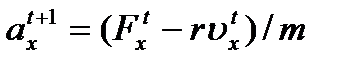 ,
,  ,
, 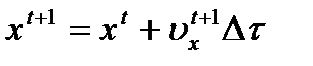 . Это состояние рассматривается как исходное и процедура расчета повторяется для момента времени
. Это состояние рассматривается как исходное и процедура расчета повторяется для момента времени  и т.д. В одном цикле с вычислениями строятся графики
и т.д. В одном цикле с вычислениями строятся графики 

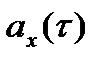 .
.
|
|
|
Большое количество физических задач сводится к анализу движения систем, имеющих две степени свободы, в частности к двумерному движе- нию материальной точки. Например, задача о качении шарика по искрив- ленной поверхности, задача о движении тела, брошенного под углом к горизонту, задача о движении частицы в поле центральных сил и т.д. Рассмотрим материальную точку массой m, движущуюся в однородном силовом поле  , на которую действует сила сопротивления
, на которую действует сила сопротивления  . Необходимо, зная начальные условия, определить координаты, проекции скорости и ускорения в последующие моменты времени, построить траекторию [8].
. Необходимо, зная начальные условия, определить координаты, проекции скорости и ускорения в последующие моменты времени, построить траекторию [8].

| Рис. 3 – Двумерное движение точки в однородном поле тяжести |
При отсутствии силы трения точка движется по параболе, а при ее наличии –– по более сложной кривой. На рис. 3.1 показаны действующие на нее силы.
По второму закону Ньютона:  , где
, где  .
.
Получаем:
 ,
, 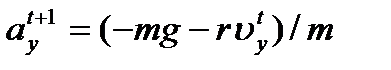 ,
, 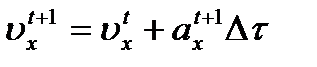 , (2)
, (2)
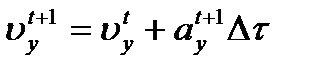 ,
,  ,
, 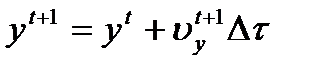 . (3)
. (3)
И так, в начале программы необходимо задать массу материальной точки m, коэффициент вязкости r, начальные координаты  ,
,  и проекции скорости
и проекции скорости 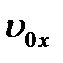 ,
,  , силовое поле
, силовое поле 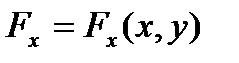 ,
, 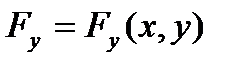 , а также шаг по времени ∆τ. Затем следует организовать цикл по времени t, в котором будут рассчитываться ускорение, скорость и координата точки в следующий момент времени t +1, и результаты вычислений будут выводиться на экран в текстовом и графическом виде. Результаты приведены на рис. 3.2. Легко определить время подъема
, а также шаг по времени ∆τ. Затем следует организовать цикл по времени t, в котором будут рассчитываться ускорение, скорость и координата точки в следующий момент времени t +1, и результаты вычислений будут выводиться на экран в текстовом и графическом виде. Результаты приведены на рис. 3.2. Легко определить время подъема 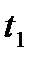 и общее время t движения материальной точки. Для этого результаты вычислений координат и времени выводят в текстовом формате. Чтобы найти время подъема следует воспользоваться тем, что в наивысшей точке траектории проекция скорости на ось y меняет свой знак на противоположный [20]. При вычислении времени полета расчеты производятся до тех пор, пока y не станет меньше нуля. Время подъема
и общее время t движения материальной точки. Для этого результаты вычислений координат и времени выводят в текстовом формате. Чтобы найти время подъема следует воспользоваться тем, что в наивысшей точке траектории проекция скорости на ось y меняет свой знак на противоположный [20]. При вычислении времени полета расчеты производятся до тех пор, пока y не станет меньше нуля. Время подъема  меньше времени спуска
меньше времени спуска 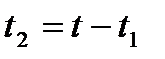
|
|
|
Рассмотрим также случай, когда материальная точка движется в центральном поле с потенциальной энергией U =U(r). На точку, удаленную от центра O на расстояние r, действует сила притяжения F = F(r), зависящая только от r и направленная к O (рис. 4.1). Можно записать:
| Рис. 4 – Движение точки в поле центральной силы |

 ,
, 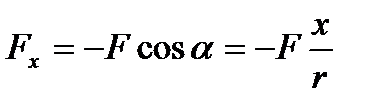 ,
, 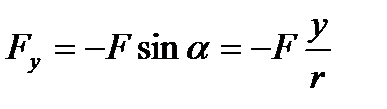 (4,5,6)
(4,5,6)
Промоделируем движение точки в поле гравитационных сил притяжения, действующих по закону обратных квадратов 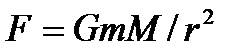 (рис. 4.2). Если действует сила вязкого трения, то точка движется по спирали, приближаясь к началу координат. Из рис. 5 видно, при малых скоростях точка движется по эллиптической орбите (траектории 1, 2, 3, 4), а при больших –– по гиперболической (траектории 5, 6). Критическому случаю соответствует параболическая траектория. На рис. 5.2 представлены результаты расчетов движения частицы в центральном поле, для которого
(рис. 4.2). Если действует сила вязкого трения, то точка движется по спирали, приближаясь к началу координат. Из рис. 5 видно, при малых скоростях точка движется по эллиптической орбите (траектории 1, 2, 3, 4), а при больших –– по гиперболической (траектории 5, 6). Критическому случаю соответствует параболическая траектория. На рис. 5.2 представлены результаты расчетов движения частицы в центральном поле, для которого 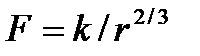 . Видно, что траекторией является незамкнутая кривая (розетка). Известно, что частица движется по замкнутой траектории только в поле квазиупругой силы или силы притяжения, для которой
. Видно, что траекторией является незамкнутая кривая (розетка). Известно, что частица движется по замкнутой траектории только в поле квазиупругой силы или силы притяжения, для которой  .
.
Для планеты, вращающейся вокруг Солнца, построим графики зависимости расстояния, линейной скорости и секториальной скорости планеты от времени и подтвердим, что секториальная скорость планеты остается постоянной (второй закон Кеплера) [21]. Пусть за время ∆τ планета перемещается из 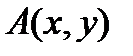 в
в  (рис. 6.1). Длины сторон AC и BC прямоугольного треугольника ABC равны:
(рис. 6.1). Длины сторон AC и BC прямоугольного треугольника ABC равны:

| Рис. 5 – Движение точки в гравитационном поле Земли |
 ,
, 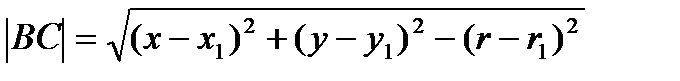 . (7)
. (7)
| Рис. 6 – Моделирование движения точки в центральном поле |
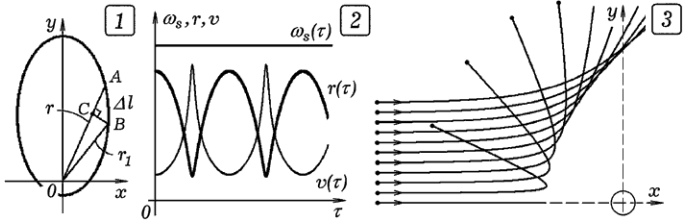
Радиус–вектор планеты заметает площадь ∆S=r|BC |/2, ее секториальная скорость ω = ∆S/∆τ. Из рис. 6.2 видно, что секториальная скорость не изменяется, это и подтверждает второй закон Кеплера. Кроме расчета секториальной скорости в программе вычисляются скорость υ и расстояния r от планеты до Солнца.
На рис. 6.3 представлены результаты расчетов движения альфа–частиц в поле положительно заряженного ядра атома (опыт Резерфорда) при различных значениях прицельного параметра ρ. Действуют силы отталкивания, поэтому в программе следует изменить знак в выражении для силы F. Траекториями частиц являются гиперболы. После небольших изменений можем промоделировать движение частицы в центральном поле, задаваемом уравнением:  . Коэффициенты
. Коэффициенты 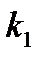 и
и  подбираются так, чтобы при больших r преобладали силы притяжения, а при малых –– силы отталкивания.
подбираются так, чтобы при больших r преобладали силы притяжения, а при малых –– силы отталкивания.
|
|
|
Итак, исходя из информации, приведенной в главе 1 можно заключить, что компьютерное моделирование, как метод научного познания является наиболее приемлемым для изучения процессов, неподвластных непосредственному изучению. К таким процессам можно отнести как микропроцессы, так и макропроцессы. В главе 2 будет рассмотрено моделирование движения электрического заряда в пространстве между заряженными пластинами конденсатора – в качестве микропроцесса, а также моделирование движения космической станции в поле тяжести Земли, Луны и Солнца.
Глава II. Методика изложения темы «Движение в поле гравитационных и электрических сил»
|
|
|
|
|
Дата добавления: 2015-08-31; Просмотров: 1211; Нарушение авторских прав?; Мы поможем в написании вашей работы!