Calcolo диференційовних електронної principii ді Calcolo Integrale, Torino 1884, № 123

Ймовірно, це було вперше виявлено Дж Thomae, Абріль етег Theorie дер complexen

Funktionen, 2-е изд., Halle 1873 р. 15; см Eneykl. d. Математика Wiss. HAI (А. Прінгсгейм, виноска 254. Наступний простий приклад було наведено в А. GENOCEHI Пеано,

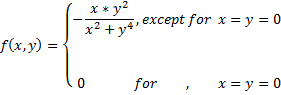
2) Лебега Х.: Ж. де Math. (6 Я, 199-200 (1905). Аналогічні спостереження найближчі максимуми і мінімуми були раніше зроблені Шеаффер, Math. Ann.35. 545-5 51 (1890).

3) Приклад такого роду є наступне:

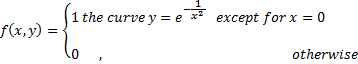
Функція f (х, у) цього типу, які, крім того, безперервною усюди, окрім чужий х = у = 0 може бути визначена аналогічно нашій формулі (2).

4) прямо. відрізок вважається приватним випадком опуклою кривою, того. дифференцируемая опукла дуга також безперервно дифференцируема см, наприклад.

Властивості кривих, застосовувані тут, слід розуміти таким чином: Нехай крива C має дотичній в р0. Візьміть цю дотичну як ξ осі з p₀ як походження. Відносно цього (ξ, η) координата системи і в досить малій околиці N р₀, крива С повинна бути представлена однозначна функція η = ȹ (ξ), яка, в першому випадку, має безперервну похідну усюди в N, і, в другому випадку, має, крім того, другу похідну, принаймні р₀.

Доказ теореми 1 виходить за допомогою наступної загальною

Теорема 2. Нехай М обмежена нескінченна безліч крапок на площині. Тоді M містить нескінченне підмножина M *, через які опукла крива С може бути закладений, який є (принаймні) один раз дифференцируема. Але не завжди існує нескінченна підмножина М, через який будь-який (принаймні) два рази дифференцируемая крива може бути закладений.

У виразі "(принаймні) один або два рази дифференцируема" фраза "(принаймні)" будуть опущені в наступному.

У § 4 і багато інших додатків цієї теореми 2 буде дано. У § 5 і 6 обговорюватимуться узагальнення функцію f з більш ніж двох змінних. Всі результати цілком аналогічно 2-вимірному випадку; але диференціюються опуклі дуги (в площині) буде замінений на диференційовних «примітивних» дуг (в просторах більшого числа вимірів). Їх визначення буде дано в § 5.

2. Докази (перша частина). Доведемо першу частину теореми 2. Нехай М обмежений нескінченна безліч точок площини, і нехай буде рахункове нескінченне підмножина M тільки з однієї точки р₀ накопичення і такі, що p₀ не відносять до А. Приєднатися p₀ з усіма точками А по прямій променів і розглянути їх межі. Нехай g промінь з p₀, який відбувається в такому межі. Якщо існує нескінченно багато точок на g, то безліч цих точок можуть бути прийняті як М * с g представляє С. В іншому випадку існує підпослідовність точок {а_r} з А, що не лежить на g, таким чином, що промені p₀a_r скликати у g Потім виберемо р₀ як походження прямокутної координатно системи з g як позитивною осі х. Нехай (х_r, у_r) координати а_r. К (abx) ми позначимо кут (≤ᴨ) між спрямованими bа прямий і позитивної осі х. Тоді можна вибрати підпослідовність {a_rk} із {а_r}, що x_rk> x_{rk + 1}> 0 і така, що кути (a_rk p₀x) є гострі і послідовність цих кутів строго убуває. Кути {a_rka_{rk + m} x) (для m=1,2,...) є. більше кута (a_rk p₀x), але сходяться до нього, як m → ∞. Тому від {a_rk} ми можемо вибрати новий підпослідовність, яку ми називаємо {b_n}, такі, що кути (b_nb_{n + 1} х) строго зменшити до 0 з ростом n. Тоді точки b_n є вершинами узагальненого опуклого багатокутника з зліченно багато сторін сходяться до р₀ і з позитивної осі х, як полукасательной в р₀. У кожній вершині b_n (з n≥2) ми звертаємо бісектрисі g_n в податливою ня від внутрішнього кута b_n-1b_nb_{n + 1}. Нехай перетин g_n і g_{n + 1} буде призначений по с_n. Гострий кут у_n визначається g_n і осі х є аріфметично середнє з кутів (b_n-1 b_nx) і (b_n b_n+1 x), і, отже, у_n зниження строго до 0 при n → ∞. Тому узагальнена багатокутник з вершинами с_n (n = 2,3,...) Також є опуклим. Його сторони c_nc_{n + 1}. (Що містить b_{n + 1}) сходяться до р₀, знову з позитивною осі х, як полукасательной з β в точці р₀.

Якщо ми закруглимо всі вершини с_n з β досить малої дузі, яка чіпає боку вершини с_n, то ми отримаємо дифференцируемая опукла дуга C з p₀ як кінцевої і позитивної осі х, як полукасательной в р₀ приєднання С з його відображенням у осі у дає дифференцируемая опукла дуга з вісь х дотичній в якості р₀. Це доводить першу частину теореми 2.

Перша частина теореми 1 випливає тепер одразу Насправді, нехай Значення f неперервна в р₀ = (x₀, y₀) на кожній дифференцируемой опуклою кривою через р₀. Тоді, якщо f (х, у) не були безперервно в точці р₀ залежно від (х, у) було б послідовність точок {а_r}, що сходяться до р₀, для яких 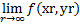існуватиме, але відрізнятиметься від f (x₀, y₀). Тоді, відповідно до сказаного вище, було б підпослідовність {a_rn}, через які можна було б закласти н дифференцируема опуклою кривою С. Таким чином, за припущенням ми мали б 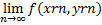= f (x₀, y₀) в суперечності з вибору {а_r}.

3. Докази (друга частина). Зараз ми покажемо, що обмежена нескінченна безліч M не завжди містить нескінченне підмножина, через які в два рази дифференцируема крива може бути закладений. Для цього розглянемо безперервну криву у = f (х), що проходить через 0 з f '(0) = 0 і з неправильною другої похідної f "(0) = + ∞; наприклад, для у = f {х) ми взяти полукубические параболу у = а * | х |^3/2 разом (а> 0) На філії цієї кривої, для якого х = 0 нехай {а_r} послідовність точок, що сходиться до походженням і нехай ця послідовність буде. наш набір М. Тоді не двічі дифференцируемая крива C не може бути прокладений через будь нескінченного підмножини M. Дійсно, нехай у = ȹ (х) з ȹ (0) = 0 і ȹ '(0) = 0 представляють таку криву C.

Тоді так, 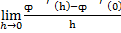= L (кінцева), для кожного ε> 0 існує δ₁> 0, що при 0 <h <δ₁ у нас |L| -ε <(ȹ '(h)) / h <| L | + ε

З іншого боку, для Q> | L | + ε існує δ₂> 0, що при 0 <h <δ₂ ми ȹ'(h)/h > Q (тобто в нашому випадку, 3 / 2а * h^-1/2 > Q). Таким чином, якщо δ = min (δ₁, δ₂) для 0 <h<δ) маємо | ȹ '(h) | <f ' (h), і, отже, по інтеграції | ȹ (h) | <f (h) для 0 <h <δ (тут, якщо f дається, δ залежить від ȹ). Таким чином, немає двічі дифференцируемая крива у = ȹ (х) може пройти нескінченно багато точок М. Це доводить другу частину теореми 2.

Друга частина теореми 1 є те безпосереднім наслідком, так як тепер можна легко привести приклади функцій f(x, y), безперервних уздовж кожної двічі дифференцируемой кривої через (0, 0), не будучи неперервна в нулі як функції (х, у). Для набору інстанції

(1)

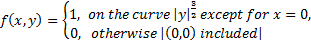
Для того щоб отримати таку функцію, яка є безперервною усюди (0,0), за винятком, можна діяти в такий спосіб. Нехай C₁, C₂, C₃ три криві з рівняннями у = а | х | ^3/2, у = б | х | ^3/2, y = c| х | ^3/2, відповідно, де б> c> a > 0. В "смуги" S обмежена С₁ і С₂, нехай буде "гора" над площиною ху чий гребінь лежить вище С₃ з постійною висоті h, крім початку координат, і яка спускається до кривих C₁ і C₂. Тепер визначимо однозначну функцію z = f (х, у) відповідно: Всередині S вона представлена в "гори", в той час як він зникає на C₁ і С₂ (походження включені) і скрізь за межами S. А дуже просто певна приклад такої функції f (х, у) є наступне:

(2)

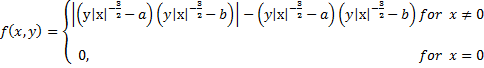
з b> а> 0. Тут крива C₃ визначається у = 1/2 (a+b) | х | ^3/2 і на С₃, крім х = 0, f має постійне значення h= 1/2 {B -a) ^2.

Ці приклади виконати те, що ми бажаємо. Насправді, кожен двічі дифференцируемая крива C проходить через початок координат 0 лежить поза S в досить малій проколеної околиці N 0, і, отже, f нулю всюди на C в N. Це також відноситься і до кожної такої кривої С, тангенс на 0 вісь х, так як по вище такої C (виключаючи 0) лежить нижче С₁ в досить малій околиці 0.

Відзначимо також, що функція F (х, у) може бути розривної в точках набору щільною в області R, хоча F неперервна на кожній кривій К в R, який двічі дифференцируема в кожній своїй точці. Приклад: Нехай (х_n,, у_n) (n = 1,2,...) послідовність усіх точок в R і координує раціональне і встановити

(3) F(x,y)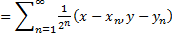

де f (х, у) позначає функцію, визначену в (2).

4. Інші додатки. Теорема 2 дозволяє багато інших додатків також.

(a) Нехай z = F (х, у) являє собою безперервну поверхню S, і нехай р₀ точкa на S. Цілком можливо, що кожна крива на S через p₀, така, що проекція на площину ху є двічі дифференцируемой крива, має дотичній в р₀ і що всі ці дотичні лежать в одній площині, але що, тим не менш, ця крива не є дотичною площиною S в точці р₀. Проте, якщо те ж саме справедливо і для кожної кривої, на S через р₀, яка проектується на, площині ху, як дифференцируемой опуклою кривою, то, що крива є дотичної площини S на р₀.

Приклад для першої частини цього твердження дається

(4) F(x,y)=f(x,y) * |x|

де f(х, у) є функція, обумовлена (2).

(b) безперервна функція ω = ȹ (z), де z = х + iу, може мати, похідне з тим самим значенням в точці z₀ вздовж кожної двічі дифференцируемой кривої через z₀, хоча ȹ '(z₀) не існує. Але ȹ '(z₀), безумовно, існує, якщо ȹ (z) має похідну з тим самим значенням в точці z₀ вздовж кожної дифференцируемой опуклою кривою.

Приклад для першої частини цього твердження виходить з функції F (х, у), визначеної в (4), встановивши ȹ (x+iy) = F (х, у).

(c) Якщо однозначна функція g(х, у) обмежена по кожній дифференцируемой опуклою кривою, що проходить через точки p₀, то g обмежена в досить малій околиці точки р₀. Но g може бути обмежена по кожній двічі дифференцируемой кривої через р₀ без обмежена в будь-який околиці р₀.

Приклад для останньої частини цього твердження дається

(5)

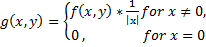
де f (х, у) знову визначає функцію, яка визначається (2).

(d) Нехай однозначна функція F (x, y) визначена в проколеної околиці р₀ ≡ (x₀, y₀).

Потім (6)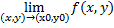

безумовно, існує, якщо f має той же межа при р₀ уздовж кожної дифференцируемой опуклою кривою через р₀. Але навіть якщо е має той же межа при р₀ уздовж кожної двічі дифференцируемой кривої через р₀, то межа (6) може не існувати.

Тут дуже важливо, щоб f завжди має той же межа при р₀. Адже навіть про існування межі f в точці р₀ (але не обов'язково завжди ж межа) уздовж кожної дифференцируемой кривої через р₀ не гарантує існування (6). Приклад: Нехай S бути частиною поверхні циліндра

x=rcosϧ, y=rsinϧ, z=ϧ, 0≤ϧ≤ᴨ/2

і нехай z = f (х, у) представляють собою поверхню, отриману шляхом продовження S по її зображенням в xz- і yz- площин.

(e) однозначна функція f(х, у) має максимум при р₀, якщо f має максимум при р₀ уздовж кожної дифференцируемой опуклою кривою через р₀. Але f може мати максимум при р₀ уздовж кожної двічі дифференцируемой кривої через р₀, не маючи максимум при р₀ залежно від (х, у). приклад:

(7) f(x,y)= (y- a|x|^3/2 )*(b|x|^3/2 –y) з b>a>0

(f) Нехай {f_r(х, у)} послідовність однозначних функцій, визначених в околиці р₀. Тоді рівномірна збіжність {f_r (х, у)} в точці р₀ випливає з рівномірною збіжності {f_r} на р₀ уздовж кожної дифференцируемой опуклою кривою через р₀: але це не обов'язково випливає з рівномірною збіжності {f_r} в р₀ уздовж кожної двічі дифференцируемой кривої через р₀.

Доказ першої частини: Нехай f_r (х, у) не є рівномірно збіжним в точці р₀. Тоді існує ε₀> 0, послідовність точок р_n = (х_n, у_n), що сходяться до р₀, і для кожного n, два індексу r_n і r_n* з r_n *> r_n ≥n, такий, що

|f_r*n (x_n, y_n) – f_rn (x_n, y_n) |≥ε_0.

Але тоді є дифференцируемая опукла C через підпослідовності {р_n}, по якій {f_r} не сходиться рівномірно на р₀.

Приклад для другої частини: зазначений

(8) ȹ(ϱ)=

And

(9) f_r (x, y) = f (x, y)* Ψ_r (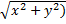 (r=1,2,3,…)

де f (х, у) є функція, обумовлена (2).

Крім того, ми наведемо приклад послідовності {F_r (х, у)} безперервних функцій в області R, рівномірно сходиться по кожній кривій в R, який двічі дифференцируема в кожній його точці, не будучи рівномірно сходиться в будь-якому субрегіоні R: Нехай (х_n, у_n) (n = 1, 2,...) послідовність усіх точок з обидві координати раціональні. Потім ми встановлюємо

(10) F_r (x,y)= 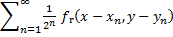(r=1,2,3,…)

де f_r (х, у) є функції, які визначаються (9).

(g) Нехай {f_r (х, у)} бути послідовність однозначних функцій, визначених у обмеженою області R. Якщо {f_r} рівномірно обмежена по кожній дифференцируемой опуклою кривою в R, то {f_r} рівномірно обмежена в R. Але {f_r} рівномірно обмежена по кожній кривій в R, який двічі дифференцируема в кожній його точці, не будучи рівномірно обмежені в R.

Приклад для. Друга частина:

(11) f_r (x,y)=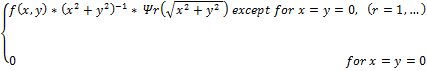

де f (х, у) і Ψ_r (ϱ) функції, які визначаються (2) і (8).

(h) ситуація абсолютно інша для послідовності {f_r (z)} регулярних аналітичних функцій в області R. Для цього. {f_r (z} рівномірно обмежені в кожній обмеженою, закритою субрегіоні R, необхідно і достатньо, щоб {f_r (z)} рівномірно обмежені на кожному замкнутому прямий сегмент R. Для то {f_r (z)} є рівномірно обмежені на кожні простих замкнутих полігонів β, що містяться в R, і, отже, по теоремі максимуму модуля, також в замкнутій області, обмеженою β.

Аналогічне твердження справедливе і для рівномірної збіжності {f_r (z)}. Це призводить або з попереднього за допомогою теореми Віталі або, зовсім прямо, використовуючи рівномірну збіжність {f_r (z)} на β, а потім закінченно, за допомогою інтегральної формули Коші, що {f_r (я)} сходиться рівномірно і в область, обмежену β.

5. Примітивні дуги. Ось і в § 6 ми обговоримо узагальнення функцій більш ніж двох змінних. Для цього ми спочатку визначити (по індукції для n≥2) примітивної дуги, які в R_n гратиме ту ж роль, опуклою дугою в площині. В R₂ примітивний дуга випукла дуга. Припустимо, поняття примітивного дуги в R_n було визначено; Потім ми визначаємо його в R_n наступним чином: нехай з дуги в R_n через точку p₀ з дотичним t0 в точці р0. Давайте ᴨ₀^{(N - 1)} бути R_n-1 через р₀ перпендикулярно t₀. Вважається примітивним дуги з дотичній t₁ в точці р₀, і ортогональна проекція С" С на площині (t₀, t₁) передбачається. Тоді ортогональна проекція С' про p₀, опукла дуга особливий випадок, в якому допущені C' стискається в точці р₀;. в цьому випадку C є прямолінійний відрізок (з t₀) Відповідно до цього визначення рекурсивної є n-1 ортогональні площини через p₀, на якій проекції C представляють собою опуклі дуги (за умови, що ніхто з них не скорочується до р₀).

Примітивна дуги C дифференцируема, якщо С має дотичній в кожній її точці. Це той випадок, при достатньо малому C, якщо і тільки якщо кожен з виступів на ортогональних площин, зазначених вище, є що диференціюється опукла дуга. Насправді, C є те навіть безперервно дифференцируема (тобто, дотичне постійно змінюється).

Сформулюємо те, що ми маємо на увазі під двічі дифференцируемой дуги C в R_n. Нехай С безперервно дифференцируема дуги через р₀ з дотичним t₀ на р₀. У досить малій околиці N на р₀, проекція С' на С на будь-якій плоскій ᴨ через t₀ є безперервно диференціюється дуги. Беручи t₀, як ξ осі з початком в точці р₀, нехай (ξ, η) координата система буде введена в ᴨ; то C' представлена в N по одноверсіонном, безперервно диференціюється функція η = ȹ (ɛ). Ми називаємо C "двічі дифференцируема", якщо, в кожній такій площині ᴨ, принаймні, ȹ'' (0) не існує.

6. Узагальнення n вимірювань. Тепер ми узагальнимо теорему 2 для n-мірного простору R_n

Теорема 3. Нехай M обмежене нескінченна безліч крапок в R_n. Тоді М містить нескінченне підмножина M*, через які дифференцируема примітивний дуги C може бути закладений. Але не завжди існує нескінченна підмножина М, через який будь двічі дифференцируемой дуга може бути закладений.

Доказ: Нехай рахункове підмножина M тільки з однієї точки p₀ накопичення і нехай р₀ не належать А. Як на початку § 2 або є лінія g, що містить нескінченне число точок А (то g можна прийняти C) або в іншому випадку ми можемо вибрати підпослідовність {a_r ¹} з таких, що промені p₀a _r ¹ сходяться до граничного променів g₁. Тоді розглянемо R_n-1, перпендикулярно g₁ на р₀ і ортогональних проекцій ã_r¹ від a_r¹, на цій R_n-1. Існує підпослідовність {a_r²} із {a_r ¹}, що промені p₀a_r² сходяться до граничного променів g₂. (Вироджений випадок, що нескінченно багато a_r¹ лежать на промені буде обговорюватися надалі} Тоді розглянемо R_n-2 (що міститься в нашій R_n-1) перпендикулярно на g₂ при р₀ і ортогональних проекцій ã_r ² в a_r² на цій R_n-2. Знову ж таки є підпослідовність {a_r³} із {a_r ²}, що промені p₀a_r³ сходяться до граничного променів g₃. Таким чином, ми як і раніше і, нарешті, прийти до послідовності {a_r^n-1} проекцій на площині R₂ перпендикулярно g_n-2 на р₀, наприклад, що промені p₀a_r^n-1 сходяться до граничного променю g_n-1. Тоді нехай g_n бути промінь в цьому R₂, перпендикулярно g_n-1 в точці р₀. Підпослідовність {a_r¹}, яка проектується в {A_r^n-1} позначається {q_r}.

Цілком можливо, що передує процедура зупиняється на більш ранній момент. Там може бути перший промінь g_k {2≤ k≤n - 1), який містить нескінченно багато проекцій ã_r^k-1; Потім ми беремо ці точки як підпослідовності {a_r^k}. Відповідний підпослідовність {a_r¹} (який ми можемо назвати {q_r} знову) Потім вже містяться в k-мірне підпростір R_n, який, натягнутого на g₁, g₂,... g_k. Тому наша процедура зупиняється тут, і ми повинні розглядати тільки випадок k-мірне.

Якщо наша процедура не зупинити на ранній стадії, то g1, g2,..., g_n промені визначити прямокутну (x₁, x₂,..., х_n) координата системи в R_n. Проекції {q_r} на (х_k, х_{k + 1}) площині позначаються {q_r^k}, (k = 1, 2,..., n-1). [Тому {q_r^n-1} збігається з {a_r^n-1}.] Згідно з теоремою 2, в (x₁, x₂) площині ми лежали дифференцируемая опукла крива С₁ через нескінченне підпослідовності {b_r¹} із {q_r¹}, Нехай {q_r^{2 *}} підпослідовність із {q_r²}, відповідна {b_r¹}. Тоді в (x₂, x₃) площині ми лежали дифференцируемая опукла крива С₂ через нескінченне підпослідовності {b_r²} із {q_r^{2 *}}. Нехай {q_r^{3 *}} підпослідовність із {q_r³}, відповідна {b_r²}. Таким чином, ми не продовжувати, поки в (х_n-1, х_n) площині, ми отримуємо дифференцируемая опукла крива С_n-1 за допомогою нескінченного підпослідовності {b_r^n-1} підпослідовності {q_r^{n-1 *}} із {q_r^n-1}, Нехай {p_r} нескінченна підпослідовність {q_r} проекції яких на кожного (х_k, х_{k+ 1}) площині включені в {b_r^k} (k = 1, 2,..., n-1). Тоді по С₁, С₂,..., С_n-1 дифференцируема примітивний дуга С визначається через точки {р_r}. Насправді, C є перетином n-1, виступаючих циліндрів.

Безпосереднім наслідком теореми 3 є наступна

Теорема 4. Один побіг узагальнив теорему 1 до однозначної функції f (x₁, x₂,..., х_n) є один замінює "опуклу криву" на "примітивної кривої".

Також легко отримати іншу Програми- теореми 3, аналогічний тим, які обговорювалися в § 4.

Дата добавления: 2015-08-31